二分查找-最基本的實現-小白初識

二分查找特別好理解，就類似於快排和歸併當中用到的分治的思想，每次取中間數與目標數相比較，然後確定是大了還是小了，區間折半。

就比如：

小紅選中了1-100中的某個數字（這個數字是56），要小明來猜，產生如下對話：

小明第一次猜測：68

小紅：大了

小明第二次猜測：35

小紅：小了

小明第三次猜測：58

小紅：大了

小明第四次猜測：49

小紅：小了

小明第五次猜測：54

小紅：小了

小明第六次猜測：56

小紅：bingo！！！

我們可以看到在上面的對話中，小明每次猜測都可以縮小區間，直到回答正確。

二分查找就是這樣的，比如我們現在有數組8，11，19，23，27，33，45，55，67，98，用二分查找如下圖：

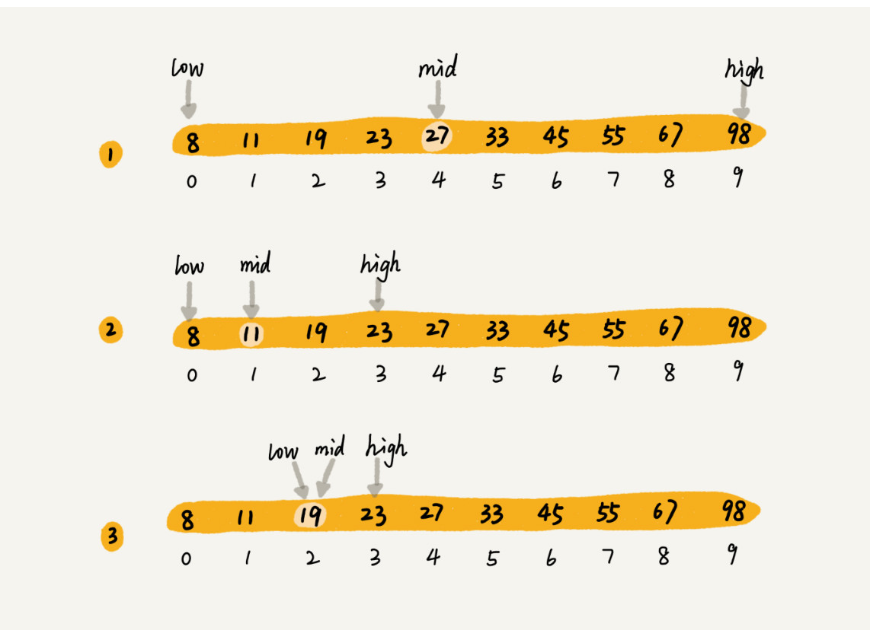
　　每次都可以縮小一半的區間，我們可以看到區間變化如下：

　　當區間大小無限接近1的時候k = log2n，所以時間複雜度為O(logn)。

　　是不是特別好理解，下麵是我用Java實現的簡單的二分查找（備註：是最簡單的實現，二分查找的變體很複雜還沒掌握）

 1 package com.structure.search;
 2 
 3 /**
 4  * 二分查找法
 5  *
 6  * @author zhangxingrui
 7  * @create 2019-02-15 21:29
 8  **/
 9 public class BinarySearch {
10 
11     public static void main(String[] args) {
12         int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
13         System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
14         System.out.println(binarySearch(nums, 50004));
15     }
16 
17     /**
18      * @Author: xingrui
19      * @Description: 二分查找法（針對有序數組且不存在重覆元素-遞歸方式實現）
20      * @Date: 21:37 2019/2/15
21      */
22     private static int binarySearch(int[] nums, int p, int r, int k){
23         if(p > r)
24             return -1;
25 
26         int mid = (p + r) / 2;
27         if(nums[mid] == k)
28             return mid;
29 
30         if(k > nums[mid])
31             return binarySearch(nums, mid + 1, r, k);
32         else
33             return binarySearch(nums, p,  mid - 1, k);
34     }
35 
36     /**
37      * @Author: xingrui
38      * @Description: 二分查找法（針對有序數組且不存在重覆元素-迴圈實現）
39      * @Date: 21:37 2019/2/15
40      */
41     private static int binarySearch(int[] nums, int k){
42         int p = 0;
43         int r = nums.length - 1;
44         while (p <= r){
45             int mid = (p + r) / 2;
46 
47             if(nums[mid] == k)
48                 return mid;
49 
50             if(k > nums[p])
51                 p = mid + 1;
52             else
53                 r = mid - 1;
54         }
55         return -1;
56     }
57 
58 }

　　代碼很簡單，其中需要註意的就是邊界條件p<=r。

　　從代碼也可以看出，簡單實現有很大的局限性，只能適用於有序的不存在重覆數據的數組。

　　並且二分查找不太適合小規模的數據查詢（因為小規模的數據查詢沒有必要），這個好理解；同時呢，也不適合太大的數據的查詢，這又是為啥子呢？

　　就是因為上面提到的：二分查找適合底層使用數組的數據，但是數組呢又是一段連續的記憶體空間，當數據很大的時候如果要用二分查找，那麼數據的底層實現就

　　只能用數組，這樣就不太好了。假設我的數據有一個G，那麼我就要申請1個G的連續記憶體空間，媽喲，怕吃飽球了。