線段樹 線段樹的每一個節點都代表一段 區間 線段樹用於維護符合結合律的的信息 (比如區間max/min、sum、xor之類的) 線段樹 在最壞的情況下效率低於分塊(大常數) 線段樹 是一顆二叉樹,對於每個父親節點(編號i)存在兩個兒子,編號分別為2i和2i+1. 建樹 1 void build(ll ...
線段樹
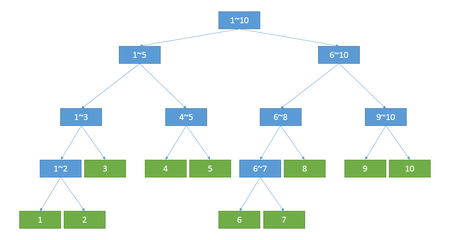
- 線段樹的每一個節點都代表一段 區間
- 線段樹用於維護符合結合律的的信息 (比如區間max/min、sum、xor之類的)
- 線段樹 在最壞的情況下效率低於分塊(大常數)
- 關於線段樹的 建樹與維護
- 線段樹 是一顆二叉樹,對於每個父親節點(編號i)存在兩個兒子,編號分別為2i和2i+1.
1 int n; 2 int ans[MAXN*4];//開四倍空間 3 inline int ls(int p){return p<<1;}//左兒子 4 inline int rs(int p){return p<<1|1;}//右兒子
- 此處的inline可以有效防止無需入棧的信息入棧,節省時間和空間。
- 二進位位左移一位代表著數值*2,而如果左移完之後再或上1,由於左移完之後最後一位二進位位上一定會是0,所以|1等價於+1(二進位運算更快)
-
建樹
1 void build(ll p,ll l,ll r) 2 { 3 if(l==r){ans[p]=a[l];return ;} 4 //如果左右區間相同,那麼必然是葉子節點啦,只有葉子節點是被真實賦值的 5 ll mid=(l+r)>>1; 6 build(ls(p),l,mid); 7 build(rs(p),mid+1,r); 8 //此處由於我們採用的是二叉樹,所以對於整個結構來說,可以用二分來降低複雜度,否則樹形結構則沒有什麼明顯的優化 9 push_up(p); 10 //此處由於我們是要通過子節點來維護父親節點,所以pushup的位置應當是在回溯時。 11 }


