一個學科體系的關鍵:公理-演繹-模型-同構、語言的嚴謹/精確/抽象 ...
最近在學習數據分析,在這裡分享一下個人的學習經驗。希望對大家有所幫助。
我理想的學習效率是這樣的:
實際上的學習效率是這樣的:

電影里的改變都是一蹴而就,順利完美,而現實往往是走一步,退半步,跌跌撞撞,把事情做到60分就謝天謝地了.
不過,最後改變世界的也是這些跌跌撞撞,一步步前行的人。
數據分析是什麼
最近要準備寒假的實習,準備找數據分析相關的工作.學習了有一個學期,最近準備把學習的內容整理一下,寫給入門者,希望如果有人對這個職業方向感興趣,可以參考,說不定可以少走一點彎路.
根據學習的總結,我覺得這樣定義更加合適:
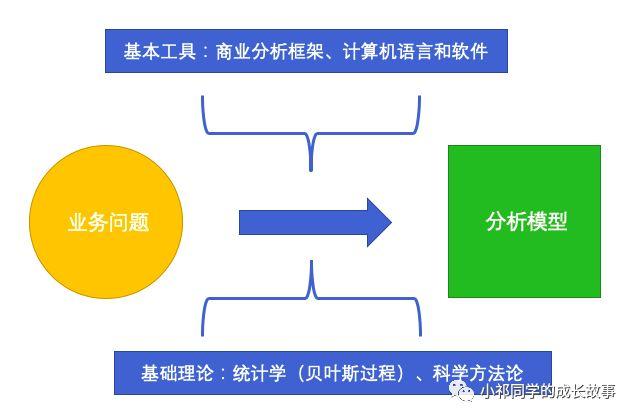
數據分析是以統計學 、科學方法論 、 商業分析框架、電腦軟體和語言為工具 ,通過將實際問題轉化為數據問題,並加以解決的一套知識體系。
七天入門數據分析
這系列的文章,目前計劃寫7篇.
七篇的結構是這樣的:
- 數據科學世界觀
- 數據分析框架概述
- 框架詳解-數據分析的數據收集與預處理
- 框架詳解-數據分析的問題分析
- 框架詳解-數據分析的模型空間建立和模型選擇
- 框架詳解-數據分析的模型優化
- 數據分析邊界-數據分析不能解決什麼?
我現在想做的,不是寫幾篇談資性質的文章,讓大家看了之後,發現'哇,數據分析好難(^-^)V'或者'靠,數據科學也不過如此'我想做的是去梳理出一個框架體系,不一定完美,但是要對前人有一個交代,對後來人有一些長遠的意義.
太史公曰:著書立說 成一家之言.
雖然達不到太史公的水平,但是可以有一樣的心愿.
一個嚴謹的學科體系是如何建立的
那麼第一個問題來了,一個嚴謹學科的體系是怎樣建立的?我們只有知道了一個嚴謹的學科是怎麼來的,才知道如何去建立一個嚴謹的體系.我們不妨來看看,世界上最嚴謹的學科體系-數學是如何梳理自己的學科脈絡的.我們普通人可能覺得數學不過就是按照實際需要分類嗎?研究概率的叫做概率論,研究統計的叫數理統計,研究圖形的叫幾何,研究數字的叫做代數,等等.但是,這隻是我們的想象,真正的數學學科分類是基於集合論的.具體是這樣的:1.首先建立一個公理體系:數學的底層公理體系大多是描述運算律的,要儘可能抽象.舉幾個例子:比如像a+b=b+a,這算公理,axb=b×a,這也是公理,a+0=a,ax1=a,等等,這就叫代數公理。還有次序公理,比如像0<1,或者是a<b,b<c,那麼a<c,等等,還有各種其他的邏輯性的公理在裡面,咱們不具體說了.2.然後就根據數學對象具體滿足哪幾條公理,來給數學對象的結構分類。比如說:假如一部分數學知識滿足A1,A2,A3和B1公理,我們就叫它代數結構。假如滿足A1,A2,A3,C1,C2的,我們就叫它拓撲結構。而且有的時候,這種數學對象只有一種結構,有的時候是多種結構同時滿足,你比如質數,它就只有序的結構,而矩陣就只有代數結構,整數集合沒有拓撲結構,像實數集合就同時擁有三種結構,代數、順序、拓撲這三種結構,就這樣分類。
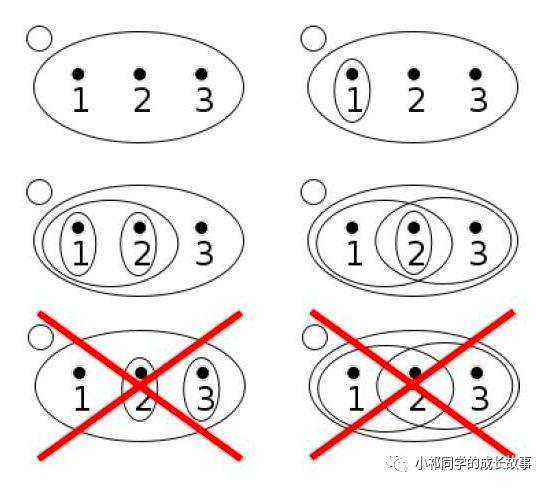

3.研究一個具體問題的時候,先研究他的集合結構,然後找到他的對應領域,然後調用這個領域的知識解決他.數學上把這個過程叫做"尋找同構問題".到這裡,大家會問為什麼我們不直接解決呢?確非要建立同構解?因為往往數學難題,之所以叫做難題,就是因為在當下的知識背景下,實在是難以解決,就好像一把很難開的鎖,我們是不可能在鎖上面直接找到鑰匙吧?如果能找到我們就直接開了,我們必須要去別的地方尋找鑰匙.在新的視角下,從前完全不是一個領域的對象,就有可能出現在同一個結構中。比如線性代數跟初等幾何這兩個東西就屬於同一種結構,簡稱同構。比如下麵的這張圖,就是一張線性代數的典型運算和初等幾何的典型運算,你可以對比一下,在沒有集合論出現之前,你很難發現其實這兩個東西是同一種結構的。

世紀難題,費馬大定理就是通過這樣的方式解決的.
最後我們總結一下,一個嚴謹的學科的建立過程
1 建立公理體系 2 根據公理體系演繹整個學科知識 3 面對具體問題,尋找符合的公理或者模型
其實這種方法也是現代科學的根基,源自歐幾裡得<幾何原本>.現代科學的另一個根基是實驗.
我們為什麼要如何清晰/抽象的定義一個概念
大家在現實生活一定會遇到這些時候:某某的本質是什麼?這個過程實際上就是我們在試圖清晰的定義一個概念.我們在建立一個學科體系的時候,另一個關鍵是要使用抽象語言描述對象,而不是自然語言.為什麼呢?好好的說人話不好嗎?為什麼要一堆符號,看著像天書?
我們需要從自然語言的誕生說起.舉個慄子,比如老師佈置作業,今天大家把練習冊上第998頁的第三題做一下,就是那道關於為什麼我最帥的題,大家一定要好好做,這道題很重要,不會做的話會影響世界和平,人們幸福,巴拉巴拉.
大家發現沒有,這一大段話,只需要用 一個公式表示就可以: 作業= 練習冊.p998.3
啊,那為什麼我們自然語言表達的時候,我們要說這麼多沒用的呢?這裡又涉及一個資訊理論的概念,信息冗餘=低損失的全面的傳播.我們通過說很多廢話,保證交流對象,儘可能的理解我們的意思.
但是這種習慣放到 科學知識上就非常尷尬了,科學追求的是凝練,概括,抽象,所以要儘可能用精確的語言描述規律.
所以我們在建立學科體系的時候,都儘可能重新定義語言使用的規範.
維特根斯坦在他的<哲學研究>里,描述過一個嚴密的語言系統,只應該包含倆類語句:X具有Y性質 (y=f(X))A,B屬於C({A,B}屬於C)
我們可以作為一個參考.
總結
這次,首先給大家預告了我的寫作計劃:7天入門數據分析
- 數據科學世界觀
- 數據分析框架概述
- 框架詳解-數據分析的數據收集與預處理
- 框架詳解-數據分析的問題分析
- 框架詳解-數據分析的模型空間建立和模型選擇
- 框架詳解-數據分析的模型優化
- 數據分析邊界-數據分析不能解決什麼?
其次,介紹了一下我接下來寫作的原則以及為什麼要這樣做
- 公理-演繹-模型-同構
- 語言的嚴謹/精確/抽象
最後講一個小故事-長使英雄淚滿襟
大家可能會問 是誰創立了數學集合論這樣的公理體系的?布爾巴基學團-數學歷史上,甚至是科學歷史上,最偉大的科學團體.
其實這是一組有情懷的法國年輕數學家的團體,他不是一個人,而是一個組織。1935年的時候,由9個差不多都是來自法國高等師範學校的數學家們組成的。

那個時候的背景是這樣的,法國曾經在達朗貝爾、拉格朗日、拉普拉斯,到後來的柯西那個年代,在數學上輝煌燦爛過100多年,這咱們之前提過,數學也曾經是法國最優秀的人從事的事業,也是法國的國學,也是法國的傳統文化。
但是在一戰中損失太慘重了,也不知道法國軍隊是怎麼考慮的,其他國家的數學家就算是參軍,主要去的也是通訊部門,或者是至少跟數學能沾點邊的,能發揮出數學家優勢的部門,比如說去算算炮彈的彈道。但是,法國不一樣,法國年輕的數學家絕大多數去了前線,都是衝鋒陷陣計程車兵,在槍林彈雨中,子彈打中了軀幹差不多就是死,所以一場大戰之後,整個法國數學的生力軍就全被消滅了。
就在1935年,法國高校的數學家們,有這幾個人,亨利嘉當、讓·迪厄多內、安德列韋伊、克勞德·謝萊瓦、德瓦薩特等等等等,一共9個人,他們就商量,
你看,現在的教授根本就不瞭解最近30年的數學進展,教科書甚至都是100年前用過的,我們要復興法國的輝煌,那麼切入點就是我們一起動手編一套涵蓋所有數學基礎,尤其是包含了最近30年數學進展的教科書,這套書要儘量全面,照顧從學生到教學部門,到研究者這三方,而且一起步,大家的計劃就是巨集偉的,計劃這套教科書要用25年的時間寫完,大致把大綱列出來,總頁數超過1200頁。而且,我們這個組織一定不能公開身份,我們就以布爾巴基為署名。成員之間身份完全平等,誰也別打算從中出名漁利,這是一件重振法國輝煌的事,大家眾志成城地就開始了。
《數學原理》是一冊一冊地出版,數學界誰都不知道布爾巴基住在哪兒,到底長什麼樣。

每次讀到這個故事,面對這樣的前人,長使英雄淚滿襟.我們一方面知道,我們之所以能走到今天是站在無數的這樣的前人的肩膀上.我們所能做的也不過是在這些偉人基礎上的修修補補,甚至連修修補補都算不上,只是把前人的智慧帶到人間而已.希望我們所做的這些,對這些前人有意義。
歡迎關註我的個人公眾號:小祁同學的成長故事。裡面還有很多這樣的文章哦。



