在理解有向圖和強連通分量前必須理解與其對應的兩個概念,連通圖(無向圖)和連通分量。 連通圖的定義是:如果一個圖中的任何一個節點可以到達其他節點,那麼它就是連通的。 例如以下圖形: 這是最簡單的一個連通圖,即使它並不閉合。由於節點間的路徑是沒有方向的,符合從任意一個節點出發,都可以到達其他剩餘的節點這 ...
在理解有向圖和強連通分量前必須理解與其對應的兩個概念,連通圖(無向圖)和連通分量。
連通圖的定義是:如果一個圖中的任何一個節點可以到達其他節點,那麼它就是連通的。
例如以下圖形:
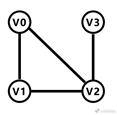
這是最簡單的一個連通圖,即使它並不閉合。由於節點間的路徑是沒有方向的,符合從任意一個節點出發,都可以到達其他剩餘的節點這一條件,那麼它就是連通圖了。
連通分量

顯然這也是一個圖,只不過是由三個子圖組成而已,但這並非一個連通圖。這三個子圖叫做這個圖的連通分量,連通分量的內部歸根還是一個連通圖。
有向圖:
在連通圖的基礎上增加了方向,兩個節點之間的路徑只能有單一的方向,即要麼從節點A連向節點B,要麼從節點B連向節點A。有向圖與連通圖(更準確來說是無向圖)最大的區別在於節點之間的路徑是否有方向。
有向圖也分兩種,一種是有環路的有向圖。另外一種是無環路的有向圖,即通常所說的有向無環圖DAG(Directed Acyclic Graph)。嚴格來說,第一種有環路的圖,如果任意一個節點都可以與其他節點形成環路,那麼它也是一個連通圖。
例如下麵的就為一個有向圖同時也是連通圖:
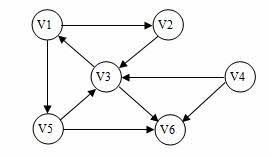
強連通分量
強連通分量SCCs(strongly connected components)是一種有向的連通圖。
如果一個圖的連通分量是它裡面所有節點到能夠彼此到達的最大子圖,那麼強連通分量SCCs就是一個有向圖中所有節點能夠彼此到達的子圖。
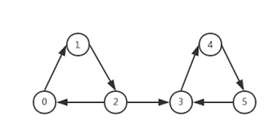
顯然由345組成的子圖是無法到達由012組成的子圖的。那麼012和345分別組成兩個強連通分量。
在實際的現實問題中,我們考慮問題可能就不會簡單地研究無向圖。例如地圖上的最短路徑規劃,ARP路由演算法等等,考慮的都是有向圖的問題。
如果有這樣一個需求,我們希望用最少的次數遍歷所有節點,怎麼處理呢?
時間效應問題,強連通分量間的時間問題。
如果有向圖的各個強連通分量中的元素個數相仿,那麼,它們內部分別進行遍歷的時間量級別是相等的,但實際情況是,這種情況很少發生。一般從一個強連通分量到另一個強連通分量。
正如上面的需求:如何用最少的次數遍歷整個有向圖的所有節點。假設我們將0、1、2組成子圖1,將3、4、5組成子圖,子圖1有一條指向子圖2的路徑。這時候,我們從子圖1的任意一點開始遍歷。假設我們從1開始遍歷,那麼遍歷的順序將會是1—2,那麼來到2的時候問題來了,是先走0的路徑還是走子圖1和子圖2之間的路徑去遍歷節點3呢?
如果我們先遍歷節點0,那麼我們遍歷完節點0之後,發現節點1已經遍歷過,就會返回節點2,再沿著子圖1和子圖2之間的路徑去遍歷子圖2。這看起來是挺合理的。
但問題是,如果是先遍歷節點3(也就是說先遍歷子圖2)呢?
假設沿著子圖1和子圖2的路徑去遍歷子圖2,那麼子圖2遍歷完後,子圖1還剩下節點0沒有被遍歷,這時候就會出現很為難的事情,因為之前遍歷的情況無法判斷哪些節點是沒有遍歷的,只能是原路返回,依次去從新遍歷,“發現”哪些節點是還沒去遍歷的。似乎上圖比較簡單,這種方法不會耗費太多的時間。但如果是節點2連接著(並指向)許多個強連通子圖的有向圖,這種“返回式”的遍歷將會是很費勁的一件事。
為瞭解決這個問題,Kosaraju演算法提出了它的解決方案。Kosaraju演算法的核心操作是將所有節點間的路徑都翻轉過來。下麵分析一下為什麼這種演算法有它的優勢。
還是拿上面的圖來講述。想象一下上面的有向圖中的所有節點間的路徑都翻轉過來了。讀者可以自己用一張紙簡單畫一下。就像下麵的圖:
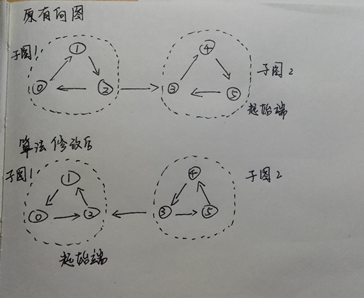
這一次,我們還是以0、1、2組成子圖1,以3、4、5組成子圖2。所不同的是,這次遍歷的起始點從子圖1開始。
多強連通分量的有向圖
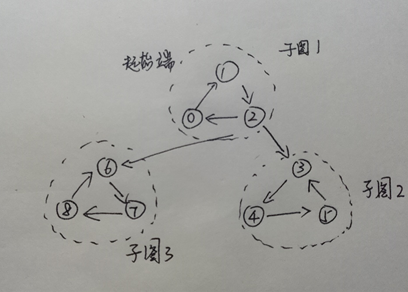
再來看一下這個多子圖的強連通圖,如果像上圖所示,從子圖1開始,就會像上文提到的那樣,遍歷到節點2,會出現多個去向的問題。而在還沒有遍歷完子圖1的前提下,從節點2過渡到子圖2/子圖3,再回溯的時候會引來較大的麻煩。通過Kosaraju演算法之後,從2節點出發的路徑都會變成指向2。此時,遍歷的起點還是從子圖1開始,由於子圖1沒有出路,就不會出現上面所說的問題。再遍歷完子圖1後,繼續遍歷子圖2、子圖3。而子圖2、子圖3的遍歷都是在強連通分量內部實現的。
演算法實現
鄰接集表示的有向圖
N={ "a":{"b"}, #a "b":{"c"}, #b "c":{"a","d","g"}, #c "d":{"e"}, #d "e":{"f"}, #e "f":{"d"}, #f "g":{"h"}, #g "h":{"i"}, #h "i":{"g"} #i }
翻轉圖實現代碼:
def re_tr(G): GT = {} for u in G: for v in G[u]: # print(GT) if GT.get(v): GT[v].add(u) else: GT[v] = set() GT[v].add(u) return GT
深度遍歷演算法實現代碼:
#遞歸實現深度優先排序 def rec_dfs(G,s,S=None): if S is None: #S = set() #集合存儲已經遍歷過的節點 S = list() #用列表可以更方便查看遍歷的次序,而用集合可以方便用difference求差集 # S.add(s) S.append(s) print(S) for u in G[s]: if u in S:continue rec_dfs(G,u,S) return S
在強連通圖內遍歷
#遍歷有向圖的強連通分量 def walk(G,start,S=set()): #傳入的參數S,即上面的seen很關鍵,這避免了通過連通圖之間的路徑進行遍歷 P,Q = dict(),set() #list存放遍歷順序,set存放已經遍歷過的節點 P[start] = None Q.add(start) while Q: u = Q.pop() #選擇下一個遍歷節點(隨機性) for v in G[u].difference(P,S): #返回差集 Q.add(v) P[v] = u print(P) return P
獲得強連通分量
#獲得各個強連通圖 def scc(G): GT = re_tr(G) sccs,seen = [],set() for u in rec_dfs(G,"a"): #以a為起點 if u in seen:continue C = walk(GT,u,seen) seen.update(C) sccs.append(C) return sccs
單元測試
print(scc(N)) 結果: {'a': None, 'c': 'a', 'b': 'c'} {'d': None, 'f': 'd', 'e': 'f'} {'g': None, 'i': 'g', 'h': 'i'} [{'a': None, 'c': 'a', 'b': 'c'}, {'d': None, 'f': 'd', 'e': 'f'}, {'g': None, 'i': 'g', 'h': 'i'}]
這是本人學習過程所寫的第一篇關於圖的演算法文章,供大家一起學習討論。其中難免會有錯誤。如有錯誤之處,請各位指出,萬分感謝!



