洛谷P1318 積水面積

題目地址: https://www.luogu.org/problemnew/show/P1318

題意簡述

給出n個柱子的高度，柱子之間的空隙可以積水，求出最大的積水面積總和。

一道很有意思的模擬題，一開始還沒有什麼思路，後來發現沒有柱子可以懸空，模擬的思路就大概出來了。

我的思路很簡單比較好想，就是把柱子分層。

例如題目中的樣例，最高的柱子高2個單位長度，那麼就把它分為2層，for迴圈遍歷每一層，我們可以發現只要是兩側有柱子的空隙就能接水，就像這個圖：

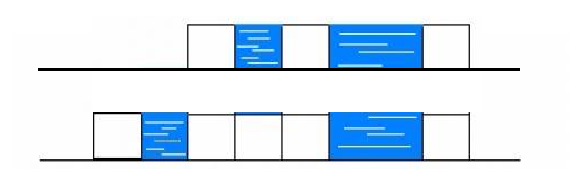
第一層可以找到3個滿足這種性質的空隙，第二層也是三個。

$ $

那如果是這樣的柱子呢：

雖然最高有2層，即分為2層，但是第二層找不出兩個柱子之間的空隙，這種情況可以直接break掉，因為這樣的情況一定是在最高層才可能出現。

所以這題就很簡單了，讀入時進行處理找到最高層，然後進行分層，很明顯層數為最高層數。然後寫一個getsum函數尋找最左端與最右端的下標，如果一樣則沒有可以接水的空隙，反之看看這段區間內有多少地方是空的

我是可愛的代碼菌OvO：

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;

inline void gi(int &x)    //get_int 快讀
{
    x=0;int t=1,k=getchar();
    for(;k<'0'||k>'9';k=getchar())if(k=='-')t=-1;
    for(;k>='0'&&k<='9';k=getchar())x=(x<<1)+(x<<3)+(k^48);x*=t;
}

const int N=10003;
int n, a[N], maxh, h;
int l, r;
bool lf=false, rf=false;
long long ans;
    
void debug()    //debug函數，可以忽略
{
      for(int i=1; i<=n; ++i)
        cout << a[i] << " ";
      puts("");
      cout << l << " " << r << endl;
      system("pause");
}

inline void getsum()    //簡陋的尋找下標函數
{
      lf=rf=false;    //判斷是否有柱子出現
      for(register int i=1; i<=n; ++i)
        if(a[i])
        {
          lf=true;
          l=i;    //最左端柱子的下標
          break;
        }
    
      for(register int i=n; i>=1; --i)
        if(a[i])
        {
          rf=true;
          r=i;    //最右端柱子的下標
          break;
        }
      return ;
}

int main(void)
{
      gi(n);
      for(int i=1; i<=n; ++i)
      {
        gi(a[i]);
        maxh=maxh < a[i] ? a[i] : maxh;    //找到最大高度，即層數
      }
      if(!maxh) goto Re;    //小優化，最高層為0一定沒有可積水的面積
      for(int i=1; i<=maxh; ++i)    //按層數依次推進
      {
        getsum();
        if(!lf || !rf) break;    //沒有找到柱子可以直接break
        for(int i=l; i<=r; ++i)
        {
          if(!a[i])
            ++ans;    //找到這一層的空隙數
        }
        for(int i=1; i<=n; ++i)
          if(a[i]) --a[i];
      //  debug();
      }
      printf("%lld", ans);
      return 0;
    
      Re:
        puts("0");
        return 0;
}

代碼是之前寫的有些地方應該不用特判也行（未嘗試）qwq