前兩篇代碼寫了初始化與查詢,知道了S函數,初始權重矩陣。以及神經網路的計算原理,總這一篇起就是最重要的神經網路的訓練了。 神經網路的訓練簡單點來講就是讓輸出的東西更加接近我們的預期。比如我們輸出的想要是1,但是輸出了-0.5,明顯不是 我們想要的。 誤差=(期望的數值)-(實際輸出),那麼我們的誤差 ...
前兩篇代碼寫了初始化與查詢,知道了S函數,初始權重矩陣。以及神經網路的計算原理,總這一篇起就是最重要的神經網路的訓練了。
神經網路的訓練簡單點來講就是讓輸出的東西更加接近我們的預期。比如我們輸出的想要是1,但是輸出了-0.5,明顯不是 我們想要的。
誤差=(期望的數值)-(實際輸出),那麼我們的誤差就是1.5。那麼我們需要縮小這個差距,就需要讓誤差的變化形成的函數的值最小。
專業點來講就是讓損失函數的導數為0。那麼首先我們需要知道我們的損失函數是一個什麼樣的函數。
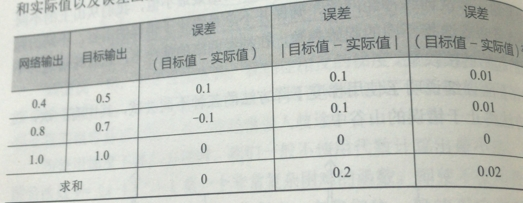
第一個候選就是(目標-實際),非常簡單明瞭的,但是以此判斷網路誤差的時候,會出現誤差為零,正負誤差相抵消了。所以這個不好。
第二個候選的是 |目標-實際|,這意味著我們的可以無視符號,誤差不能相抵消,可是由於在最小值附近的時候是一個V字形,所以到不了最小的值,只能左右徘徊,也不太好
第三個候選的是 (目標-實際)^2,二次函數是平滑連續的,求導容易計算,越接近最小值斜率越小,方便調節步長。
誤差函數用來乾什麼呢?以後再講
綜上我們決定在這三個裡面選擇第三個損失函數,但是還有其他的複雜的又去的損失函數,可以自行探索。
現在我們知道我們的誤差了。那麼這個誤差來自哪裡呢?
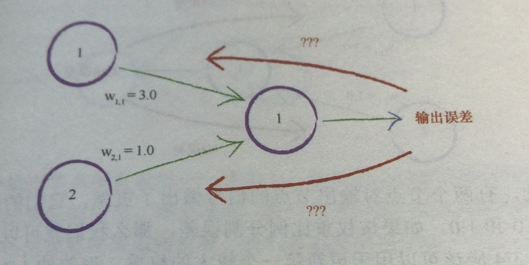
如圖可以看到,我們的輸出誤差是由之前的數值和權重相乘導致的,那麼我們的誤差的來源應該是權重成正比的。
比如兩個節點權重分別是3.0與1.0,那麼我們輸出誤差的3/4應該分給權重大的節點,1/4分給權重小的節點。
然後我們把這個思想擴展到多個節點,如果我們隱藏層有100個節點,按照每條鏈接的權重的比例,相應分配輸出的誤差,
這個就是反向傳播,BP(back propagation)。
隱藏層第一個節點的誤差就是

我們假設輸出的誤差為0.8與0.5,重要的是計算過程,權重就隨機吧。
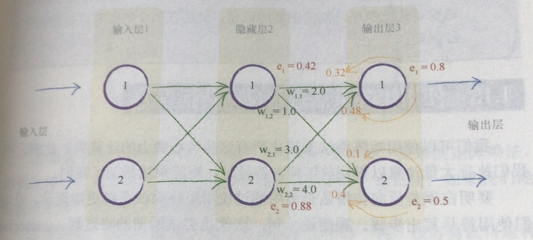
然後將這種反向傳播到更前面的層。
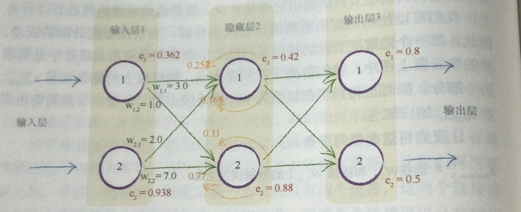
那麼我們就從最後的輸出一層一層,將前面所有的誤差全都算出來。
可是很明顯這種計算是十分費時費力的,這就有要用到我們的矩陣運算了。
首先是用輸出的誤差計算隱藏層的誤差
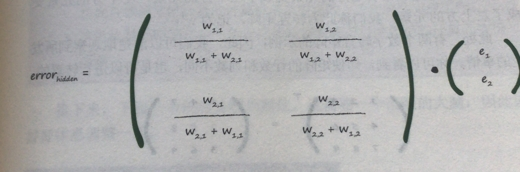
右邊的e1,e2就是輸出的誤差。權重比例矩陣點乘輸出的誤差,新矩陣就是隱藏層的每個節點的誤差的列矩陣了。
但是很明顯分母太礙事了。而帶上分母只是表示這一條鏈路的權重與相比於其他連在這個輸出節點的鏈路上的占比,
簡單一點的說法就是這個分母是用來標準化的。不看它,我們僅僅失去了後饋誤差的大小(這裡我沒理解,我困擾了好久,為什麼可以沒有)
我們可以用簡單容易的方法來辨認。
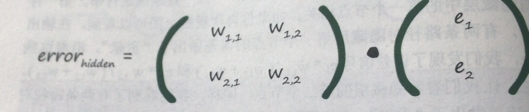
這和我們之前的權重矩陣與輸入矩陣相乘感覺很相似
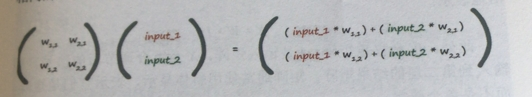
正好就是我們正向計算時候的權重矩陣的轉置,也方便我們代碼的書寫
用簡潔的寫法寫出來就是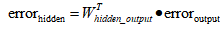
最後就是原代碼中train函數的一部分的撰寫。我們需要把我們的輸入以及正確的結果(用來計算誤差)來作為參數
前半部分和查詢函數一樣,就是計算給定輸入對應輸出的數值。然後反向計算各層各節點的誤差。
#訓練神經網路 def train(self,inputs_list,targets_list): #給函數輸入列表以及正確的輸出列表 inputs = np.array(inputs_list,ndmin=2).T #輸入列表轉成array數組並轉置成列向量用來計算 targets = np.array(targets_list,ndmin=2).T #正確輸出的列表轉成array數組並轉置成列向量用來計算 #計算隱藏層的輸入 hidden_inputs = np.dot(self.wih,inputs) #計算隱藏層的輸出,代入S函數 hidden_outputs = self.activation_function(hidden_inputs) #計算輸出層的輸入 final_inputs = np.dot(self.who,hidden_outputs) #計算輸出層的輸出,代入S函數 final_outputs = self.activation_function(final_inputs) #誤差是(目標-實際) #(目標-實際)^2是誤差函數,用來減小誤差,而不是誤差本身 output_errors = targets - final_outputs #隱藏層誤差 hidden_errors = np.dot(self.who.T,output_errors) #權重函數轉置矩陣點乘乘以輸出誤差矩陣 pass
可以看到我們辛辛苦苦講了這麼多的東西用,代碼倒是沒幾行。尤其是那個計算各個節點的誤差
只用了
#隱藏層誤差 hidden_errors = numpy.dot(self.who.T,output_errors) #權重函數轉置矩陣點乘乘以輸出誤差矩陣
就完成了,這裡還是要特別說明一下,輸入層是沒有誤差的,輸入層只做輸入!
迄今為止所有的代碼

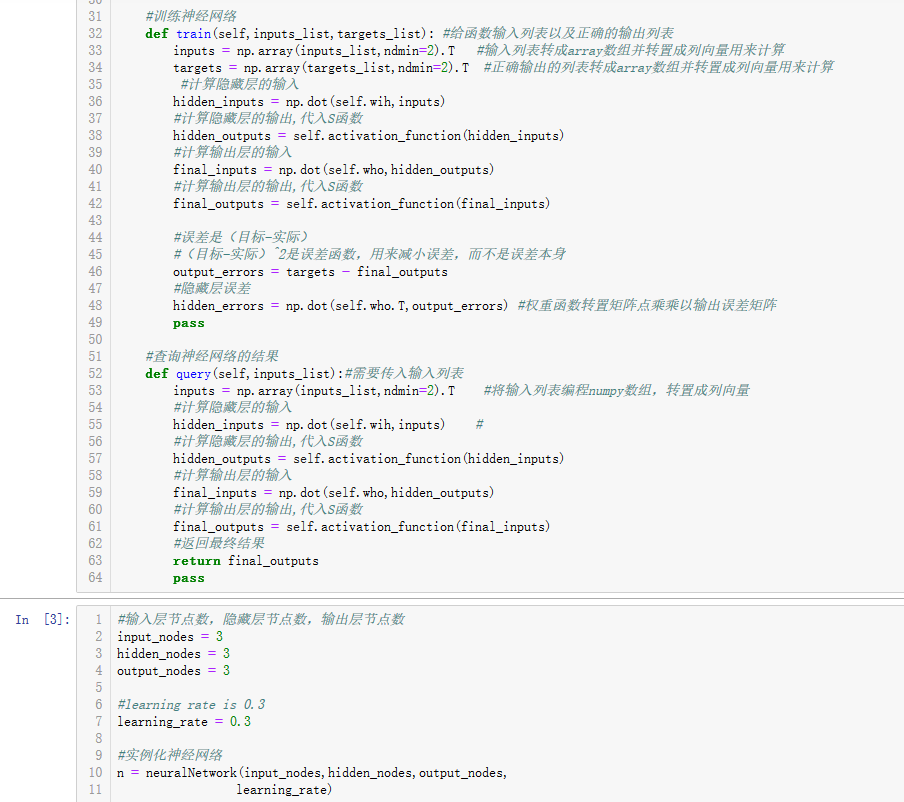
import numpy as np import scipy.special #神經網路類定義 class neuralNetwork: #初始化神經網路 def __init__(self,inputnodes,hiddennodes,outputnodes, learningrate): #設置的是輸入層節點數,隱藏層節點數,輸出層節點數 self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #設置學習率 self.lr = learningrate #初始化權重函數 #初始化輸入層到隱藏層的權重矩陣 # self.wih = np.random.rand(self.hnodes,self.inodes)-0.5 #-0.5為了能出現負數 # #初始化隱藏層到輸出層的權重矩陣 # self.who = np.random.rand(self.onodes,self.hnodes)-0.5 #按照均值為0,標準方差為傳入鏈接數的根號的倒數的正態分佈的隨機取樣,獲得更好的初始化權重 #初始化輸入層到隱藏層的權重矩陣 self.wih = np.random.normal(0.0,pow(self.hnodes,-0.5),(self.hnodes,self.inodes))#pow就是標準方差的表示形式 #初始化隱藏層到輸出層的權重矩陣 self.who = np.random.normal(0.0,pow(self.onodes,-0.5),(self.onodes,self.hnodes)) #設置激活函數 self.activation_function = lambda x:scipy.special.expit(x) pass #訓練神經網路 def train(self,inputs_list,targets_list): #給函數輸入列表以及正確的輸出列表 inputs = np.array(inputs_list,ndmin=2).T #輸入列表轉成array數組並轉置成列向量用來計算 targets = np.array(targets_list,ndmin=2).T #正確輸出的列表轉成array數組並轉置成列向量用來計算 #計算隱藏層的輸入 hidden_inputs = np.dot(self.wih,inputs) #計算隱藏層的輸出,代入S函數 hidden_outputs = self.activation_function(hidden_inputs) #計算輸出層的輸入 final_inputs = np.dot(self.who,hidden_outputs) #計算輸出層的輸出,代入S函數 final_outputs = self.activation_function(final_inputs) #誤差是(目標-實際) #(目標-實際)^2是誤差函數,用來減小誤差,而不是誤差本身 output_errors = targets - final_outputs #隱藏層誤差 hidden_errors = np.dot(self.who.T,output_errors) #權重函數轉置矩陣點乘乘以輸出誤差矩陣 pass #查詢神經網路的結果 def query(self,inputs_list):#需要傳入輸入列表 inputs = np.array(inputs_list,ndmin=2).T #將輸入列表編程numpy數組,轉置成列向量 #計算隱藏層的輸入 hidden_inputs = np.dot(self.wih,inputs) # #計算隱藏層的輸出,代入S函數 hidden_outputs = self.activation_function(hidden_inputs) #計算輸出層的輸入 final_inputs = np.dot(self.who,hidden_outputs) #計算輸出層的輸出,代入S函數 final_outputs = self.activation_function(final_inputs) #返回最終結果 return final_outputs pass #輸入層節點數,隱藏層節點數,輸出層節點數 input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #learning rate is 0.3 learning_rate = 0.3 #實例化神經網路 n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate)



