作者作為一個蒟蒻,也是最近才自學了線段樹,不對的地方歡迎大佬們評論,但是不要噴謝謝 好啦,我們就開始說說線段樹吧 線段樹是個支持區間操作和查詢的東東,平時的話還是蠻實用的 下麵以最基本的區間加以及查詢區間和為例 線段樹顧名思義就是棵樹嘛,葉子節點是每個基本點,它們所對應的父親就是它們的和,具體如下圖 ...
作者作為一個蒟蒻,也是最近才自學了線段樹,不對的地方歡迎大佬們評論,但是不要噴謝謝
好啦,我們就開始說說線段樹吧
線段樹是個支持區間操作和查詢的東東,平時的話還是蠻實用的
下麵以最基本的區間加以及查詢區間和為例
線段樹顧名思義就是棵樹嘛,葉子節點是每個基本點,它們所對應的父親就是它們的和,具體如下圖
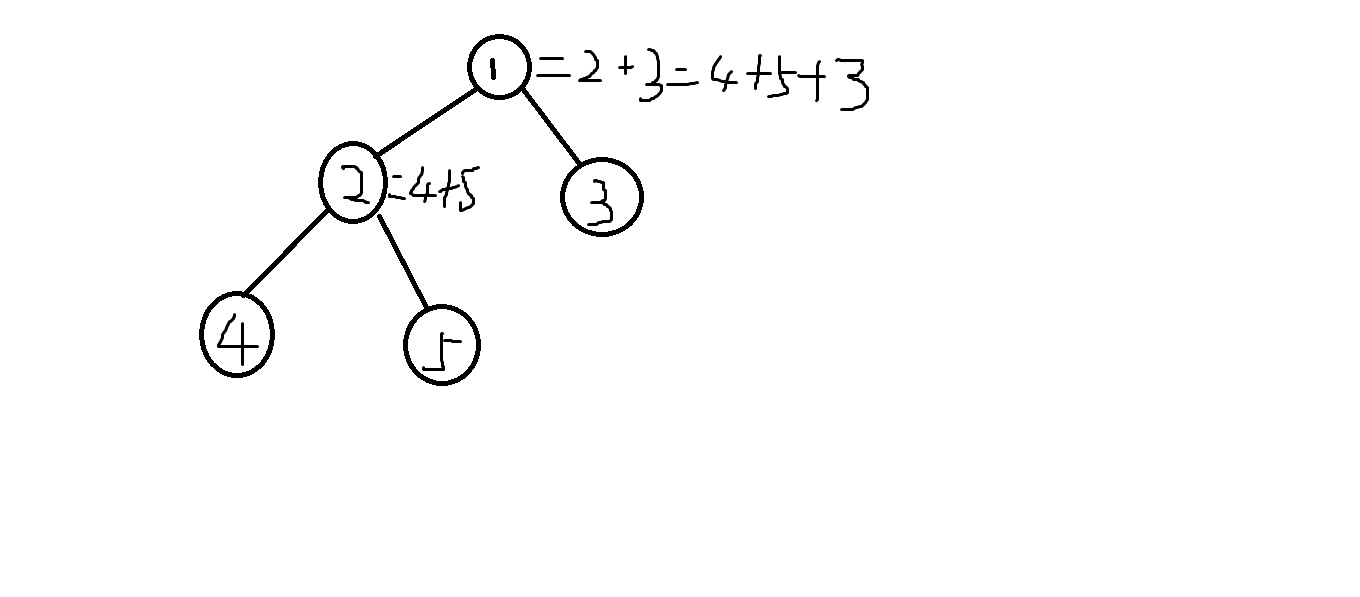
但是對於這樣的線段樹來說,操作所需的時間是遠達不到我們的要求的(會被t),因為我們會進行一些不必要的操作,就像如果沒有查詢到某個點,那麼就沒有必要去修改這個點的值,為此,我們會引入一個懶標記,記錄每個基本點需要被加上的值(稱為add),那麼樹上任意一個點需要增加的值=該點對應的區間長度*add
那麼總的來說,線段樹的基本操作我個人認為可以分成3個,建樹、修改和查詢,當然如果繼續細分也是口以(可以)的,就比如說還可以分出 區間和的向上傳遞(父親節點等於子節點的和)和懶標記的向下傳遞(子節點的懶標記=原來的懶標記+父節點的懶標記)
所以接下來我們就來看看建樹、修改和查詢這3部分的具體代碼吧(深呼吸)
首先是建樹(build)
#define ls 2*rt,l,(l+r)/2 //left son #define rs 2*rt+1,(l+r)/2+1,r //right son #define ll long long void build(ll rt,ll l,ll r)//rt是當前點,l和r代表l到r區間的和 { if(r==l) //也就是說,我們找到了一個葉子節點,自己到自己的和 就是自己嘛 { scanf("%lld",&su[rt]);//那我們就輸入這個節點的值 } else//否則就去看看當前點的左右兒子 { build(ls);//看左兒子 build(rs);//看右兒子 //當rt的左右兒子都準備好了,我們就可以求出rt的值了 su[rt]=su[2*rt]+su[2*rt+1]; } return; } //一層一層的求,我們就可以建好一個初步的樹啦
然後是修改(change)
#define ls 2*rt,l,(l+r)/2 //左右兒子,和之前一樣 #define rs 2*rt+1,(l+r)/2+1,r #define ll long long void change(ll rt,ll l,ll r,ll L,ll R,ll add) //當前點,當前區間的左右端點,需要修改的區間的左右端點,需要給每個基本點加上的值 { if(l>=L&&r<=R)//如果說當前區間是需要修改區間的子集 { su[rt]+=add*(r-l+1); //那麼就修改當前點,註意乘上當前區間長度 o[rt]+=add;
//記得修改懶標記 return;//別忘了返回! } if(o[rt]!=0) //如果說我們恰好經過了一個被打上懶標記的點,那不如就順手把它的懶標記下傳好了 { //修改左右兒子的值 su[rt*2]+=o[rt]*((r+l)/2-l+1);// (r+l)/2是區間中點 su[rt*2+1]+=o[rt]*(r-(r+l)/2);//實際應乘以(r-((r+l)/2+1)+1)但+1-1抵消了 o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; //下傳懶標記註意是加上父節點的懶標記不是等於 o[rt]=0;//清除懶標記 } if(L<=(l+r)/2) //二分思想,如果需要修改的區間左端點在當前區間中點的左邊,即當前區間中點左側有需要修改的點的話 { change(ls,L,R,add);//那就去修改啊 } if(R>(l+r)/2)//同理 { change(rs,L,R,add); } su[rt]=su[2*rt]+su[2*rt+1];//橘氏春秋有雲(什麼鬼):有下就有上,改完記得上傳 return; }
呼啊,已經完成2/3了,堅持就是勝利!↖(^ω^)↗
查詢(find)
void find(ll rt,ll l,ll r,ll L,ll R) //當前點,當前區間左右端點,需要查詢的區間左右端點 { if(l>=L&&r<=R)//如果當前區間是查詢區間的子集 { ans[c]+=su[rt];//答案就加上當前點的值 } else//不然就找找它應該在那個區間裡面 { if(o[rt]!=0)//順便下傳rt的懶標記 { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2)//二分思想,如果左邊有點 { find(ls,L,R);//那就找找左邊 } if(R>(l+r)/2)//如果右邊有點 { find(rs,L,R);//那就找找右邊 } su[rt]=su[2*rt]+su[2*rt+1];//還是那句老話,橘氏春秋有雲:有下就有上 } return;//看到return我就開心↖(^ω^)↗ }
哇吼,結束了才怪,接下來是總代碼!
//線段樹要寫成lazy[i]+=lazy[祖先]的形式 //溫馨提示,炒雞重要,我這個蒟蒻就被坑了嚶嚶嚶 #include<iostream> #include<cstdio> #define ls 2*rt,l,(l+r)/2 #define rs 2*rt+1,(l+r)/2+1,r #define ll long long using namespace std; int n,m,a,c; ll su[400005],x,y,k,ans[100005],o[400005];//數組開4倍 void build(ll rt,ll l,ll r) { if(r==l) { scanf("%lld",&su[rt]); } else { build(ls); build(rs); su[rt]=su[2*rt]+su[2*rt+1]; } return; } void change(ll rt,ll l,ll r,ll L,ll R,ll add) { if(l>=L&&r<=R) { su[rt]+=add*(r-l+1); o[rt]+=add; return; } if(o[rt]!=0) { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2) { change(ls,L,R,add); } if(R>(l+r)/2) { change(rs,L,R,add); } su[rt]=su[2*rt]+su[2*rt+1]; return; } void find(ll rt,ll l,ll r,ll L,ll R) { if(l>=L&&r<=R) { ans[c]+=su[rt]; } else { if(o[rt]!=0) { su[rt*2]+=o[rt]*((r+l)/2-l+1); su[rt*2+1]+=o[rt]*(r-(r+l)/2); o[rt*2]+=o[rt]; o[rt*2+1]+=o[rt]; o[rt]=0; } if(L<=(l+r)/2) { find(ls,L,R); } if(R>(l+r)/2) { find(rs,L,R); } su[rt]=su[2*rt]+su[2*rt+1]; } return; } int main() { scanf("%d %d",&n,&m);//n個基本點,m次操作 build(1,1,n); for(int i=1;i<=m;i++) { scanf("%d",&a); if(a==1)//我們要進行區間加啦 { scanf("%lld %lld %lld",&x,&y,&k);//在x到y上加k change(1,1,n,x,y,k); // for(int i=1;i<=2*n;i++)cout<<" "<<i<<"="<<su[i]; // cout<<"\n"; // 寫給需要調試的小可愛的 } if(a==2)//查詢 { c++;//個人喜歡統一輸出,c記錄第幾次詢問 scanf("%lld %lld",&x,&y);//查詢x到y的和 find(1,1,n,x,y); } } for(int i=1;i<=c;i++) { printf("%lld\n",ans[i]);//統一輸出答案 } }
這樣,一棵完完整整的基礎簡化版的線段樹就寫完了
有問題的話可以問呦~雖然我也不一定會但是我會儘力解答的!
感謝閱讀



