基礎演算法 - 二分與三分 - 蒟蒻複習基礎

　　二分是一種常用而且非常精妙的演算法，常常是我們解決問題的突破口。二分的基本用途是在單調序列或單調函數中做查找操作。因此，當問題的答案具有單調性時，就可以通過二分把求解轉化為判定（根據複雜度理論，判定的難度小於求解）。進一步的，我們還可以通過三分（適用於求解凸性函數）解決單峰函數的極值以及相關問題。

• 二分

　　思想：分而治之。將一個規模為n的問題分解為k個規模較小的子問題，這些子問題互相獨立且與原問題相同，(如果子問題的規模仍然不夠小,，再劃分為k個子問題)，然後遞歸的求解這些子問題，最後用適當的方法將各個子問題的解合併成原問題的解。

　　方法：a）二分查找：在一個單調有序的集合或函數中查找一個解，每次分為左右兩部分，判斷解在哪個區間（並調節上下界），並直到找到目標元素。

int binary_search(int x) {
    int l = 0, r = n;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (a[mid] == x) {
            return mid;
        }
        if (a[mid] < x) {
            l = mid + 1;
        } else {
            r = mid;
        }
    }
    return - 1;
}

　　　　   b）二分答案：（最大值最小或最小值最大這類問題）這類雙最值問題常常選用二分法求解（二分之後，先假裝自己確定答案），配合貪心，DP等演算法，檢驗這個答案是否合理，將最優化問題轉化為判定性問題。

　　　　   c）代替三分：（對於單峰函數）二分導函數求函數極值。

　　例題：Bzoj1734   Poj2018 ... ... 

　　借書（2018沈陽集訓Day4 - 二分答案)

　　題目描述

　　輸入

　　輸出

// 二分答案
#include <iostream>
#include <algorithm>
using namespace std;
long long diff[100010];
long long n, m, tmp, num_book;
bool check (long long x) {
    num_book = 1;
    long long tmp = diff[1];
    long long flag_one = 1;
    while (num_book < m) {
        long long next = tmp + x;
        long long flag = lower_bound(diff + flag_one, diff + n + 2, next) - diff;
        if (flag == n + 1) {
            return false;
        }
        num_book += 1;
        flag_one = flag;
        tmp = diff[flag];
    }
    return true;
}
int main() {
    freopen("margin.in", "r", stdin);
    freopen("margin.out", "w", stdout);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> diff[i];
    }
    sort(diff + 1, diff + n + 1);
    long long l = 0;
    long long r = diff[n];
    long long ans;
    diff[n + 1] = 2 * diff[n];
    while (l <= r) {
        long long mid = (l + r) / 2;
        if (check(mid) == true) {
            ans = mid;
            l = mid + 1;
        } else if (check(mid) == false) {
            r = mid - 1;
        }
    }
    cout << ans << endl;
    return 0;
}

• 三分

　　適用於凸性函數的極值問題（二次函數就是一個典型的單峰函數）。與二分法強調函數的單調性不同，三分法強調函數的單峰性。

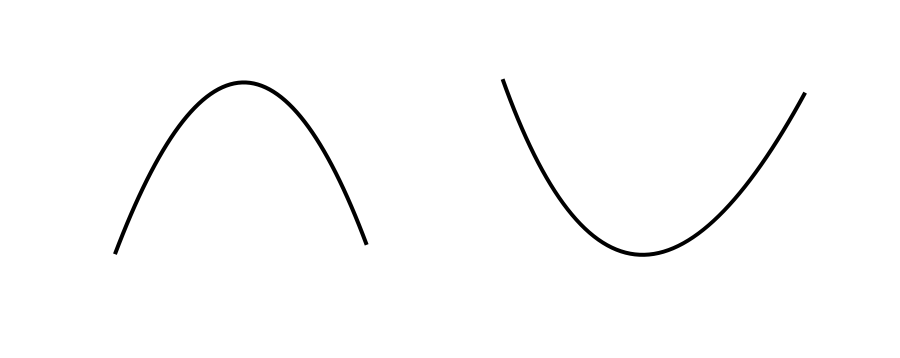
　　在區間 [L,R] [L,R] 中找兩個三分點，也就是 mid 和 mmid，然後比較這兩個點的 y 值大小。如果是計算最大值的情況，那麼 y (mid) ≤ y (mmid)，說明最大值肯定在 mid 右邊，這時把區間變成 [mid , R]，反之變成 [L , mmid] ，直到 LL 和 RR 很接近為止。如果是求最小值的情況就反過來。

double cal() {
    double l = 0, r = pi / 2;
    while (r - l > eps) {
        double mid = (l + r) / 2;
        double mmid = (mid + r) / 2;
        if (f(mid) < f(mmid)) {
            l = mid;
        }
        else {
            r = mmid;
        }
    }
    return l;
}

• 二分快速冪

　　c/c++ 的 <math> 庫中有 pow 函數（pow(double a, double b)），但一般都是用來計算浮點數的，函數的時間複雜度是 O(b) 。有些時候，a，b 都是整數，且 b 比較大（1e8），我們肯定需要一些優化方法，那就是快速冪。

　　快速冪有很多種寫法，但是結合二分的思想，無疑比遞歸要快很多。

　　（先放個遞歸的薛洋）

// 遞歸
int pw1(int x, int y, int p) { 
    if (!y) {
        return 1;
    }
    int res = pw1(x, y / 2, p);
    res = res * res % p;
    if (y & 1) {
        res = res * x % p;
    }
    return res;
}

　（再放個能治他的二分曉星塵）

// 二分
int pw2(int x, int y, int p) {
    int res = 1;
    while (y) {
        if (y & 1) {
            res = res * x % p;
        }
        y >>= 1;
        x = x * x % p;
    }
    return res;
}

　　 皮這一下我很開心 Orz