在開始先來看一個有意思的東西: 結果是負數!!!! 這個結果理論上是非常不應該的,這已經違背了我們的常識,畢竟正數的乘積,最後的結果應該還是一個正數,但是這裡出現負數的情況,雖然結果不對,但是好在即使我們各種交換順序,結果都是一致的 我們再來試試浮點數呢 從結果看浮點數好像也沒好到哪裡去,也算錯了, ...
在開始先來看一個有意思的東西:
root@localhost: lldb (lldb) print (500 * 400) * (300 * 200) (int) $0 = -884901888 (lldb) print ((500 * 400)* 300) * 200 (int) $1 = -884901888 (lldb) print ((200 * 500) * 300) * 400 (int) $2 = -884901888 (lldb) print 400 * (200 * (300 * 500)) (int) $3 = -884901888 (lldb)
結果是負數!!!! 這個結果理論上是非常不應該的,這已經違背了我們的常識,畢竟正數的乘積,最後的結果應該還是一個正數,但是這裡出現負數的情況,雖然結果不對,但是好在即使我們各種交換順序,結果都是一致的
我們再來試試浮點數呢
root@localhost: lldb (lldb) print (3.14 + 1e20) - 1e20 (double) $0 = 0 (lldb) print 3.14 + (1e20 - 1e20) (double) $1 = 3.1400000000000001 (lldb)
從結果看浮點數好像也沒好到哪裡去,也算錯了,這個時候你肯定和我一樣在想,電腦機電腦,你一個以計算文明著稱的東東也計算不對了,也太不靠譜了,其實出現這種情況是有原因的,不知道你小時候有沒有和我一樣拿著家裡的計算器上讓幾個非常的大的數連著相乘,最後發現結果也是現實的亂七八糟,還給你不停的報錯誤錯誤,哎想想當時如果多思考思考,去探究探究說不定自己早已經成為大神了,哈哈哈.....
言歸正傳,電腦是用有限數量的為來對一個數字編碼的,所以當結果太大以至於不能表示時,運算就會出現類似上面兩種情況的錯誤,這裡稱為溢出(這裡先有一個概念)。
整數運算和浮點運算會有不同的數學屬性是因為它們處理數字表示有限性的方式不同。整數的表示雖然只能編碼一個相對小的數值範圍,但是這種表示是精確的,浮點數雖然可以編碼一個較大的數值範圍,但是這種表示是近似的
由上面這個小問題來引出這次的內容,來好好探究探究操作系統是如何在表示和處理這些信息,為什麼會出現溢出,為什麼會計算錯誤,如何在自己以後寫代碼的過程中避免一些潛在的問題,讓自己寫出更高質量的代碼
我們學習一門開發語言的時候,開始學習基礎語法的時候都會學習各種數據類型,這些數據類型在系統中又是如何存儲的呢?接著往下看。
信息的存儲
二進位 十六進位 十進位
這裡關於十進位和十六進位的轉換有一個挺有意思的地方:
當值x是2的非負整數n次冪時,也就是x = 2n,可以非常容易的將x寫成十六進位形式
其實我們看這個時候x的二進位就是1後面跟了n個0,而十六進位數字0表示4個二進位0
先來看看幾個轉換:
當x = 32 即32 = 2^5, 5 = 4*1 + 1 轉換成十六進位為0x20
當x = 64 即64 = 2^6, 6 = 4*1 + 2 轉換為十六進位為0x40
當x = 128 即128 = 2^7 7 = 4*1 + 3 轉換為十六進位為0x80
當x = 256 即 256 = 2^8 8 = 4*2 + 0 轉換為十六進位為0x100
當x = 512 即 512 = 2^9 9 = 4*2 +1 轉換為十六進位為0x200
當x = 1024 即 1024 = 2^10 10 = 4*2 + 2 轉換為十六進位為0x400
所以從上面的規律可以將公式總結為i+4j j就是後面0的個數,而最前的數就是2的i次方
字數據大小
字長,指明指針數據的標稱大小,虛擬地址是以這樣一個字來編碼的,字長決定了虛擬地址空間的最大大小。
我們老是聽到別人說系統是32位,系統是64位的,其實就是和這個相關,如果是32位的機器虛擬地址的範圍為:
0-2^32-1 程式最多訪問2^32個位元組,64位同理,這裡你也就明白了64位能夠支持更大的記憶體空間,32位字長限制虛擬地址空間為4千兆位元組即4GB,這也是早起很多電腦的標配,因為32位的系統,你安裝再多的記憶體,你右鍵電腦屬性,看到識別的依然只是不到不到4GB,而64位的虛擬地址空間為16EB,所以你能支持更多的記憶體。
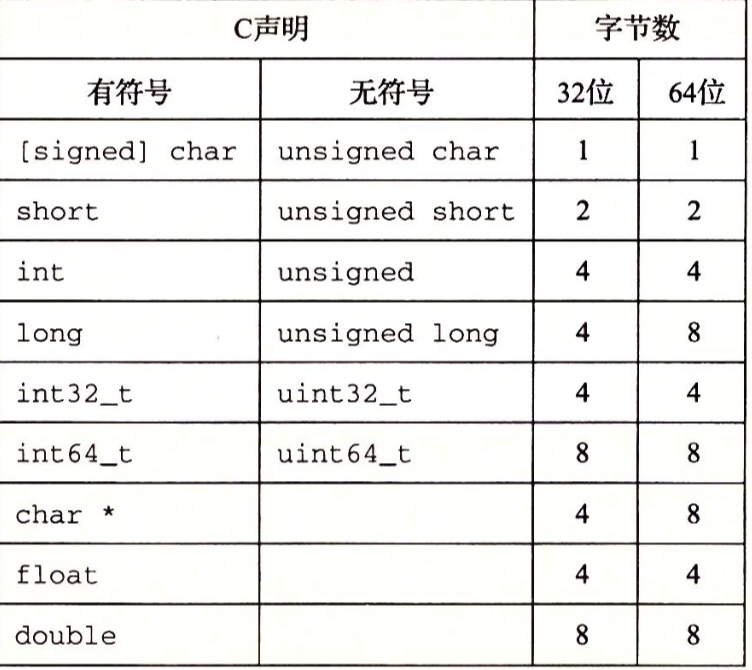
上圖是32位和64位典型值,整數或者有符號的,即可以表示負數,零和正數;無符號的只能表示非負數
定址和位元組順序
在大多數計算器上,對於多位元組對象都被存儲為連續的位元組序列,對象的地址為所使用位元組中最小的地址,這裡有個例子假設一個int的變數x的地址為0x100 也就是地址表達式&x 的值為0x100 那麼x的4個位元組將被存儲在記憶體0x100,0x101,0x102和0x013位置
而這個地址就涉及到一個概念就是定址的問題,這裡兩種方式:大端法和小端法
假設變數x 的類型為int, 位於地址0x100 它的十六進位值為0x01234567 地址範圍0x100-0x103的位元組序列兩種定址方式如下圖表示:
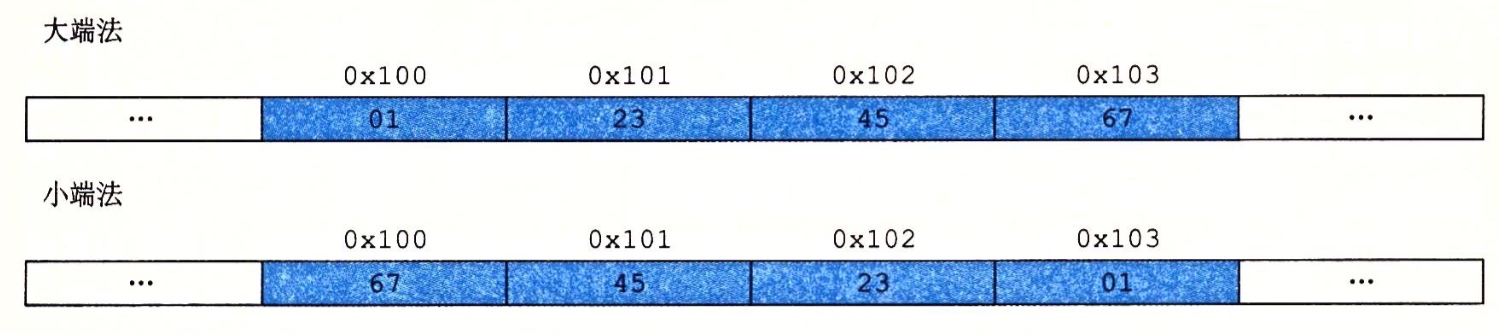
大端法和小端法 對我們大多數程式員其實是不可見的,我們也很少關心這個東西,但是在以下三種情況是需要註意的:
第一種:不同類型的機器之間通過網路傳遞二進位數據時,也就是當小端法機器給大端法機器發數據或者返回來發送數據,在接收數據的時候,位元組順序對接收者來說都是反的,所以為了避免這個問題出現,網路應用程式的代碼編寫應該遵守已經建立的關於位元組順序的規則
第二種:主要是於都表示整數數據的位元組序列時位元組順序也是非常重要,主要發生在檢查機器級程式時。
第三種:當編寫規避正常的類型系統的程式時。在C語言中通常會使用強制類型轉換cast或者聯合union來允許一種數據引用一個對象,而這種數據類型與創建這個對象時定義的數據類型是不同的。
其實上面三種情況我們作為一名普通的開發者也很少回去關註,畢竟高級語言已經對做了更高級的抽象,同時替我們也做了很多事情來規避一些錯誤的發生
在這部分的練習題中有個挺有意思的題:
這裡已經計算的出整數3510593的十六進位為0x00359141
而浮點數3510593.0的十六進位為0x4A564504
我們先看看這兩個十六進位的二進位表示分別為:
00000000001101011001000101000001
*********************
01001010010101100100010100000100
我們發現中間有星號的部分是完全一樣的,並且我們整數的除了最高位1,其他所有位都嵌在浮點數中,這是巧合麽,當然不是啦,繼續深入研究
表示字元串
C語言中字元串被編碼為一個以null其值為0字元結尾的字元數組,每個字元都由某個標準編碼來表示
最常見的是ASCII字元編碼,使用ASCII碼作為字元碼的任何系統上都將得到相同的結果,與位元組順序和字大小無關。也正是這樣文本數據比二進位數據具有更強的平臺獨立性
表示代碼
其實我們的代碼在不同類型的機器上編譯時,生成的結果也是不同的,所以你在linux上編譯的代碼肯定是不能再windows上運行的,反之亦然
布爾代數
與 And:A=1 且 B=1 時,A&B = 1
或 Or:A=1 或 B=1 時,A|B = 1
非 Not:A=1 時,~A=0;A=0 時,~A=1
異或 Exclusive-Or(Xor):A=1 或 B=1 時,AB = 1;A=1 且 B=1 時,AB = 0
對應與集合運算則是交集、並集、差集和補集,假設集合 A 是 {0, 3, 5, 6},集合 B 是 {0, 2, 4, 6},全集為 {0, 1, 2, 3, 4, 5, 6, 7}
& 交集 Intersection {0, 6}
| 並集 Union {0, 2, 3, 4, 5, 6}
^ 差集 Symmetric difference {2, 3, 4, 5}
~ 補集 Complement {1, 3, 5, 7}
邏輯運算
C語言提供了邏輯運算符|| && ! 分別對應命題邏輯中的OR AND NOT 運算
邏輯運算任務所有非零的參數都表示TRUE, 而參數0表示FALSE
邏輯運算符和對應的位級運算的第二個重要區別是:如果對第一個參數求值就能確定表達式結果,那麼邏輯運算符就不會對第二個參數求值
位移運算
表達式x << k 表示x想左移動k位 ,x向左邊移動k位,丟棄最高的k位,併在有點補k個0
表示是x << k 這個分兩種:邏輯右移(左邊補0) 和算術右移(右邊補符號位)
現在幾乎所有的編譯器或者機器組合都對有符號使用算術右移面對無符號數,右移必須是邏輯的
整數的表示
我們對整數主要分為:有符號和無符號
先記一些術語:

關於32位程式上C語言以及64位程式上C語言的典型取值範圍:
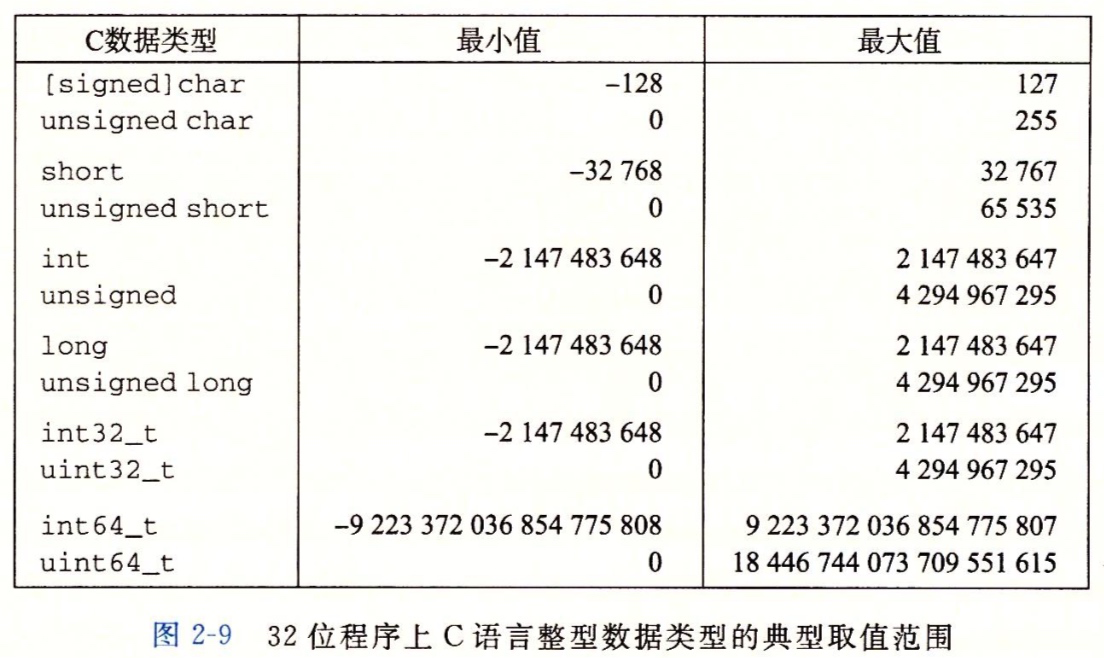

在上面兩個圖中我們都可以看出負數的範圍比正數的範圍大1,為啥會這樣的,繼續往下看
無符號數的編碼
下麵是幾種情況B2U 給出的從為向量到整數的映射
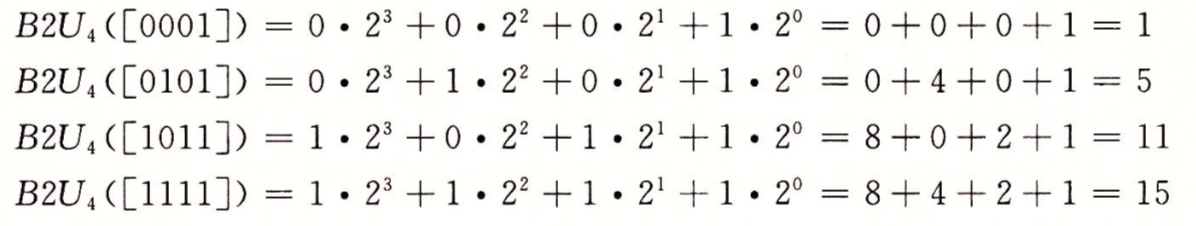
所以我們可以考慮w位所能表示的值的範圍,最小值用位向量表示[000...0] ,也就是整數值0
而最大值的表示則是2^w - 1
補碼編碼
其實在很多時候我們還是希望用到負數,最常見的有符號的電腦表示方式就是補碼形式
最高有效位解釋為負權 用函數B2T表示補碼編碼
最高有效位稱為符號位,它的權重為-2^w-1 是無符號表示中權重的負數
符號位被設置為1 時,表示為負,當設置為0 時表示為非負,通過下麵理解:

這個時候再看補碼所能表示的值的範圍:
最小值的的位向量為[1000...0] 其整數值為-2^w-1
最大值的位向量為[01111...1] 其整數值為2^w-1 - 1
我們還是以4位表示:
TMin = B2T([1000]) = 2^3 = -8
TMax = B2T([0111]) = 2^2 + 2^1 + 2^0 = 4+2+1 = 7
同無符號表示一樣,在可表示的取值範圍內的每個數字都有一個唯一的w位的補碼編碼
這個屬性總結為一句話:補碼編碼的唯一性
小結:其實我們通過上面的無符號的編碼和補碼編碼就可以看出,補碼的範圍是不對稱的
|TMin| = |TMax| + 1
我們學習編程語言的時候,一般在基礎部分都會講到關於整數和負數的表示範圍,尤其是強類型語言中
當時總是說負數表示的最大範圍一直被-1 當時很多時候老師都會告訴你是因為符號位占了一位,當時可能是一個模糊的概念,為啥是符號位占了一位,從補碼的這個概念,其實你就應該完全明白了為啥符號位占了一位
其次這裡我們還可以知道一個規律就是無符號數值剛好比補碼的最大值的2倍 再加1:UMax = 2TMax + 1

有符號和無符號之間的轉換
c語言允許在各種不同的數字數據之間做強制類型轉換
其實在c語言中,強制類型的轉換的結果是保持位值不變,只是改變瞭解釋這些位的方式
-12345 的16 位補碼表示與53191 的16位無符號表示是一樣的
上面數字太大了,通過簡單的數字來表示,可能更好理解:
對於數字16 ,二進位表示為1111 十六進位表示為0xF
這個時候的UMax 的值為:16,TMin 的值為:-8,Tmax 的值為7
其實這個時候還有一個有意思的點是,如果就是這個4位的話,表示-1 的表示方式:
二進位形式為:1111 發現其實和 最大的無符號數的表示方式是一樣的
所以在c語言中,假設我們定義了一個無符號的數 u= 4194967295 ,如果我們通過(int)u 進行強制轉換,我們得到的結果就是-1,代碼內容如下:
#include <stdio.h> int main() { unsigned u = 4294967295u; int tu = (int)u; printf("u=%u,tu=%d\n",u,tu); return 0; }
程式的列印的結果和我們上面說的是一致的,這裡需要知道的是4294967295 這個數字是32位能表示的最大數字,即這個是32位中的Umax
再看一個代碼:
#include <stdio.h> int main() { short int v = -12345; unsigned short uv = (unsigned short)v; printf("v = %d, uv = %u\n",v, uv); return 0; }
從執行結果可以看出v = -12345, uv = 53191
從上面的兩個例子,都可以看出強制類型轉換的結果都是保持位值不變,只是改變瞭解釋這些位的方式
並且我們知道的是-12345 的16位補碼表示與53191的16位無符號表示是完全一樣的。我們代碼中將short強制類型轉換為unsigned short 改變了數值,但是不改變位表示
小結:
對於大多數C語言的實現,處理同樣的字長的有符號和無符號數之間相互轉換的一般規則是:
數值可能會改變,但是位模式不變
這裡位是固定的,假設為w位,給定0<=x<=UMax 範圍內的一個整數x, 函數U2B 會給出x的唯一的w位無符號表示,同樣的,當x滿足TMin<=x <=TMax 函數T2B 會給出x的唯一的w位的補碼表示
現在將函數T2U 定義為T2U = B2U 也就是這個函數的輸入是一個TMin - TMax 的數,而結果得到的是一個0-UMax的值,這裡兩個數有相同的位模式,除了參數是無符號的,而結果是以補碼表示的
同樣的對於0-UMax 之間的值x ,定義函數U2T 為U2T = B2T 生成一個數的無符號表示和x的補碼表示相同

從上圖我們可以看出T2U(-12345) = 53191 並且 U2T(53191) = -12345
所以十六進位表示寫作0xCFC7 的16位位模式及時-12345的補碼表示,又是53191的無符號表示。同時我們需要註意12345 + 53191 = 65536 = 2^16
也就是說,無符號表示中的UMax 有著和補碼表示-1相同的位模式,這兩者之間的關係:1+UMax(w) = 2^w 註意:這裡的w表示位數
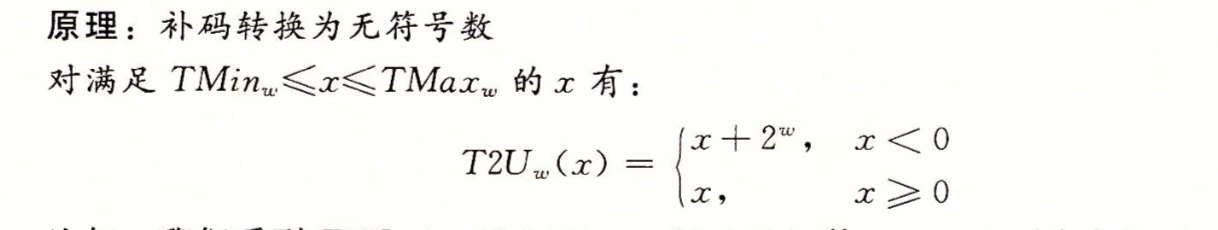
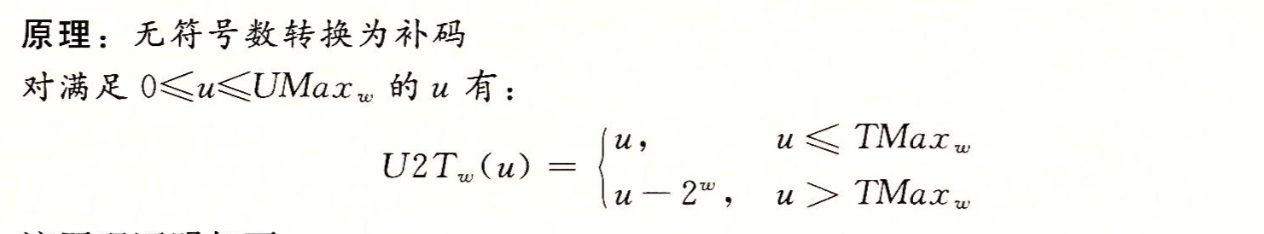
擴展一個位表示
一個常見的運算是在不同的字長的整數之間轉換,同時保持數值不變。
但是如果目標數據類型太小以至於不能表示想要的值時,就會出問題了,然而,從一個較小的數據類型轉換到一個比較大的類型,總是可以的
要將一個無符號數轉換為一個更大的數據類型,只需要在表示的開頭添加0 這種運算被稱為零擴展
要將一個補碼數字轉換為一個更大的數據類型,只需要在表示的開頭添加最高有效位的值,這種運算稱為符號擴展
可以通過下麵的例子理解:
給出字長w= 3 到w = 4的符號擴展的結果位向量[101]表示值-4+1=-3,因為這裡是對補碼的擴展,所以應用的是符號擴展,得到為向量[1101] 表示的值-8+4+1 = -3 擴展之後我們得到的值還是-3 ,類似的向量[111] 和[1111]都表示-1
截斷數字
我們在代碼中通常有時候都會用到強制轉換,即將高位向低位轉換

總結
有符號到無符號的隱式強制轉換會導致某些非直觀的錯誤,從而導致我們自己的程式出現我們意想不到的錯誤
並且這種包含隱式強制類型轉換的細微差別很難被髮現。
通過代碼可能更好理解:
這個代碼中,函數sum_elements好的參數length 為數組a的長度,如果我們正常賦值這個代碼不會有任何問題,但是如果在整個項目中,你傳遞參數的時候,length傳遞的不是數組a的長度,而傳遞了0 這個時候length -1 就會變成負數,但是最開始我們定義length的時候定義的是無符號的,所以就會變成當前位數的最大值即UMax 所以《= 是總是滿足條件的,這個時候你再取數組的值的時候就會超出數組的最大長度,程式就會出現異常錯誤。
#include <stdio.h> float sum_elements(float a[], unsigned length) { int i; float result = 0; for (i =0; i< length -1; i++) result = a[i]; printf("%f",result); return result; } int main(){ float a[5] = {1.1,2.3,1.4,3.22,1.24}; sum_elements(a,5); }
其實上面的這個情況也是有符號到無符號數的隱式轉換會導致錯誤或者漏洞的方式,避免這類錯誤的一種方法就是絕對不使用無符號數,而實際上除了C以外也很少語言支持無符號整數


