二分搜索樹的深度優先遍歷和廣度優先遍歷

二分搜索樹的特點

　　二分搜索樹首先是一個二叉樹，其次其必須滿足的條件是：每個節點的鍵值必須大於其左子節點，每個節點的鍵值必須小於其右子節點，這樣以左右孩子為根的子樹仍為二分搜索樹，需要註意的是，二分搜索樹不一定是一顆完全二叉樹。

深度優先遍歷

　　深度優先遍歷的基本思想：對每一個可能的分支路徑深入到不能再深入為止，而且每個結點只能訪問一次。深度優先遍歷的非遞歸的通用做法是採用棧。要特別註意的是，二分搜索樹的深度優先遍歷比較特殊，可以細分為前序遍歷、中序遍歷、後序遍歷。

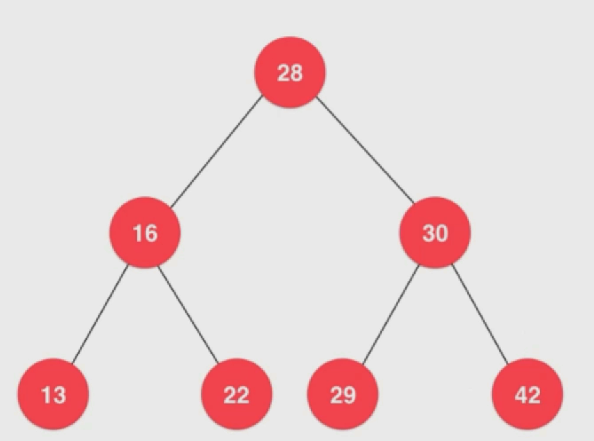
廣度優先遍歷

　　深度優先遍歷的基本思想：從上往下對每一層依次訪問，在每一層中，從左往右（也可以從右往左）訪問結點，訪問完一層就進入下一層，直到沒有結點可以訪問為止。廣度優先遍歷的非遞歸的通用做法是採用隊列。

　　例如，對於上面的這個二分搜索樹，其層序遍歷（廣度優先遍歷）結果是：28 16 30 13 22 29 42。

Java代碼實現深度優先遍歷和廣度優先遍歷

　　下麵採用Java語言來構建這個二分搜索樹，並且實現前序遍歷、中序遍歷、後序遍歷三種不同方式的深度優先遍歷和廣度優先遍歷（層序遍歷）。

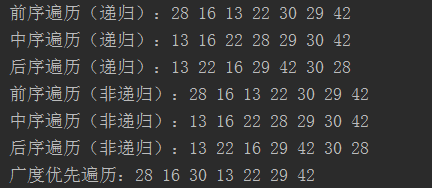
  1 package com.allSorts;
  2 
  3 
  4 import java.util.LinkedList;
  5 import java.util.Queue;
  6 
  7 /**
  8  * Created by Demrystv.
  9  */
 10 public class BSTTraverseTest {
 11 
 12     public static void main(String[] args) {
 13         BinarySearchTree<Integer> tree = new BinarySearchTree<Integer>();
 14         tree.insertNode(28);
 15         tree.insertNode(16);
 16         tree.insertNode(13);
 17         tree.insertNode(22);
 18         tree.insertNode(30);
 19         tree.insertNode(29);
 20         tree.insertNode(42);
 21         System.out.print("前序遍歷（遞歸）：");
 22         tree.preOrderTraverse(tree.getRoot());
 23         System.out.println();
 24         System.out.print("中序遍歷（遞歸）：");
 25         tree.inOrderTraverse(tree.getRoot());
 26         System.out.println();
 27         System.out.print("後序遍歷（遞歸）：");
 28         tree.postOrderTraverse(tree.getRoot());
 29         System.out.println();
 30         System.out.print("前序遍歷（非遞歸）：");
 31         tree.preOrderTraverseNoRecursion(tree.getRoot());
 32         System.out.println();
 33         System.out.print("中序遍歷（非遞歸）：");
 34         tree.inOrderTraverseNoRecursion(tree.getRoot());
 35         System.out.println();
 36         System.out.print("後序遍歷（非遞歸）：");
 37         tree.postOrderTraverseNoRecursion(tree.getRoot());
 38         System.out.println();
 39         System.out.print("廣度優先遍歷：");
 40         tree.breadthFirstTraverse(tree.getRoot());
 41     }
 42 
 43 
 44     /**
 45      * 結點
 46      */
 47     public static class Node<E extends Comparable<E>> {
 48         E value;
 49         Node<E> left;
 50         Node<E> right;
 51         Node(E value) {
 52             this.value = value;
 53             left = null;
 54             right = null;
 55         }
 56     }
 57 
 58     /**
 59      * 使用一個前序遍歷構建一棵二分搜索樹
 60      */
 61     public static class BinarySearchTree<E extends Comparable<E>> {
 62         private Node<E> root;
 63         BinarySearchTree() {
 64             root = null;
 65         }
 66         public void insertNode(E value) {
 67             if (root == null) {
 68                 root = new Node<E>(value);
 69                 return;
 70             }
 71             Node<E> currentNode = root;
 72             while (true) {
 73                 if (value.compareTo(currentNode.value) > 0) {
 74                     if (currentNode.right == null) {
 75                         currentNode.right = new Node<E>(value);
 76                         break;
 77                     }
 78                     currentNode = currentNode.right;
 79                 } else {
 80                     if (currentNode.left == null) {
 81                         currentNode.left = new Node<E>(value);
 82                         break;
 83                     }
 84                     currentNode = currentNode.left;
 85                 }
 86             }
 87         }
 88         public Node<E> getRoot(){
 89             return root;
 90         }
 91         /**
 92          * 前序遍歷二分搜索樹（遞歸）
 93          * @param node
 94          */
 95         public void preOrderTraverse(Node<E> node) {
 96             System.out.print(node.value + " ");
 97             if (node.left != null)
 98                 preOrderTraverse(node.left);
 99             if (node.right != null)
100                 preOrderTraverse(node.right);
101         }
102         /**
103          * 中序遍歷二分搜索樹（遞歸）
104          * @param node
105          */
106         public void inOrderTraverse(Node<E> node) {
107             if (node.left != null)
108                 inOrderTraverse(node.left);
109             System.out.print(node.value + " ");
110             if (node.right != null)
111                 inOrderTraverse(node.right);
112         }
113         /**
114          * 後序遍歷二分搜索樹（遞歸）
115          * @param node
116          */
117         public void postOrderTraverse(Node<E> node) {
118             if (node.left != null)
119                 postOrderTraverse(node.left);
120             if (node.right != null)
121                 postOrderTraverse(node.right);
122             System.out.print(node.value + " ");
123         }
124         /**
125          * 前序遍歷二分搜索樹（非遞歸），用的是棧
126          * @param root
127          */
128         public void preOrderTraverseNoRecursion(Node<E> root) {
129             LinkedList<Node<E>> stack = new LinkedList<Node<E>>();
130             Node<E> currentNode = null;
131             stack.push(root);
132             while (!stack.isEmpty()) {
133                 currentNode = stack.pop();
134                 System.out.print(currentNode.value + " ");
135                 if (currentNode.right != null)
136                     stack.push(currentNode.right);
137                 if (currentNode.left != null)
138                     stack.push(currentNode.left);
139             }
140         }
141         /**
142          * 中序遍歷二分搜索樹（非遞歸），用的是棧
143          * @param root
144          */
145         public void inOrderTraverseNoRecursion(Node<E> root) {
146             LinkedList<Node<E>> stack = new LinkedList<Node<E>>();
147             Node<E> currentNode = root;
148             while (currentNode != null || !stack.isEmpty()) {
149                 // 一直迴圈到二叉排序樹最左端的葉子結點（currentNode是null）
150                 while (currentNode != null) {
151                     stack.push(currentNode);
152                     currentNode = currentNode.left;
153                 }
154                 currentNode = stack.pop();
155                 System.out.print(currentNode.value + " ");
156                 currentNode = currentNode.right;
157             }
158         }
159         /**
160          * 後序遍歷二分搜索樹（非遞歸），用的是棧
161          * @param root
162          */
163         public void postOrderTraverseNoRecursion(Node<E> root) {
164             LinkedList<Node<E>> stack = new LinkedList<Node<E>>();
165             Node<E> currentNode = root;
166             Node<E> rightNode = null;
167             while (currentNode != null || !stack.isEmpty()) {
168                 // 一直迴圈到二叉排序樹最左端的葉子結點（currentNode是null）
169                 while (currentNode != null) {
170                     stack.push(currentNode);
171                     currentNode = currentNode.left;
172                 }
173                 currentNode = stack.pop();
174                 // 當前結點沒有右結點或上一個結點（已經輸出的結點）是當前結點的右結點，則輸出當前結點
175                 while (currentNode.right == null || currentNode.right == rightNode) {
176                     System.out.print(currentNode.value + " ");
177                     rightNode = currentNode;
178                     if (stack.isEmpty()) {
179                         return; //root以輸出，則遍歷結束
180                     }
181                     currentNode = stack.pop();
182                 }
183                 stack.push(currentNode); //還有右結點沒有遍歷
184                 currentNode = currentNode.right;
185             }
186         }
187         /**
188          * 廣度優先遍歷二分搜索樹，又稱層次遍歷，用的是隊列
189          * @param root
190          */
191         public void breadthFirstTraverse(Node<E> root) {
192             Queue<Node<E>> queue = new LinkedList<Node<E>>();
193             Node<E> currentNode = null;
194             queue.offer(root);
195             while (!queue.isEmpty()) {
196                 currentNode = queue.poll();
197                 System.out.print(currentNode.value + " ");
198                 if (currentNode.left != null)
199                     queue.offer(currentNode.left);
200                 if (currentNode.right != null)
201                     queue.offer(currentNode.right);
202             }
203         }
204     }
205 }

　　運行結果如下，與前面理論分析完全對應。