1.引言 2.位運算基礎 3.位運算在角色許可權設計中的應用 4.為什麼in32的範圍是-2^31 ~ 2^31-1 ? 5.同餘的概念 6.模的概念幫助理解補數和補碼。 一、引言 這周在做一個新增角色許可權需求時,遇到下麵這樣一行代碼,這篇文章將圍繞這行代碼展開。 二、位運算基礎 關於位運算的基礎知識 ...
1.引言
2.位運算基礎
3.位運算在角色許可權設計中的應用
4.為什麼in32的範圍是-2^31 ~ 2^31-1 ?
5.同餘的概念
6.模的概念幫助理解補數和補碼。
一、引言
這周在做一個新增角色許可權需求時,遇到下麵這樣一行代碼,這篇文章將圍繞這行代碼展開。
user.RoleType = ~(~user.RoleType | 511) | requestDTO.Role;
二、位運算基礎
關於位運算的基礎知識參見:
百度百科:https://baike.baidu.com/item/%E4%BD%8D%E8%BF%90%E7%AE%97
維基百科:https://zh.wikipedia.org/wiki/%E4%BD%8D%E6%93%8D%E4%BD%9C
總結如下:
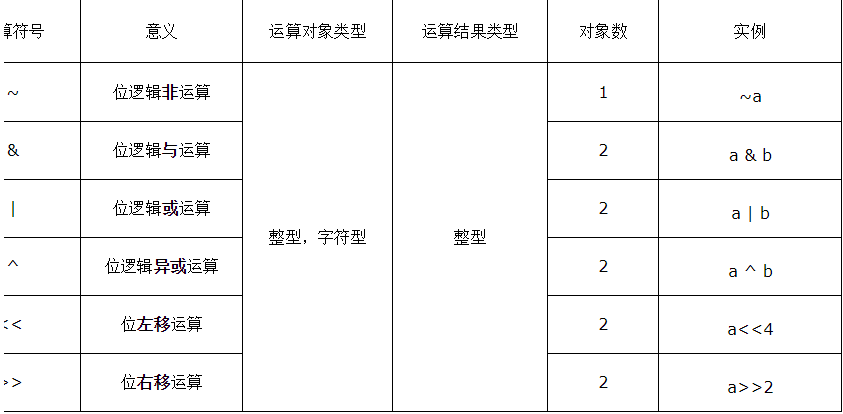
三、位運算在角色許可權設計中的應用(優缺點)
業務場景:有A.B.C.D四個基礎角色,現在需要新增一個複合角色(架構師),可以配置用戶。
下麵是一個demo例子,位運算在角色許可權中的應用
[Flags] public enum RoleType { /// <summary> /// 無角色 /// </summary> [Description("無角色")] None = 0, /// <summary> /// 普通用戶角色 /// </summary> [Description("普通用戶")] A = 1, /// <summary> /// 初級開發 /// </summary> [Description("初級開發")] B = 2, /// <summary> /// 中級開發 /// </summary> [Description("中級開發")] C = 4, /// <summary> /// 高級開發 /// </summary> [Description("高級開發")] D = 8, /// <summary> /// 架構師 /// </summary> [Description("架構師")] E = 8 } public class UnitTest1 { public static void Test1() { var a = RoleType.A | RoleType.B; //變數a為 A | B var b = RoleType.B | RoleType.D; //變數b為 B | D var aa = a.ToString();//變數aa為 "A,B" var bb = a & (~RoleType.A);//從組合狀態中去掉一個元素A ,結果為 枚舉 B var bb1 = ~(~a | RoleType.A); //bb結果等價於bb1 var cc = (b & RoleType.B) != 0;//檢查組合狀態是否包含枚舉 B var dd = RoleType.A | RoleType.B | RoleType.B | RoleType.B; //變數dd為 A | B } }
分析:
1.為什麼枚舉角色數都是2的倍數?
十進位 二進位
1 01
2 10
4 100
8 1000
。。。。。。
我們發現在各個位上值都是唯一的,所以做位或運算時,不同值的運算結果是唯一的;反過來,我們也可以根據結果值推算出來包含的枚舉(即業務中的角色)
ok,到這裡我們再看開頭引言中的那行代碼,可以寫為
user.RoleType = (user.RoleType & ~511) | requestDTO.Role;
抽象為x=(x&~y)|z,就是去除x中的y角色,再與z做位或組合。
想下,這個在保存用戶角色的時候會很巧妙,就是去除用戶 x(原有角色)中的 y(基礎角色),再和z(要保存的角色),做位或運算組合 得出一個新的要保存角色。
優點:一個roletype欄位可以保存用戶的所有角色信息
缺點:當已經有31個角色,當需要再新增角色的時候,就變的尷尬了(超出了int32位)
解決辦法:
1.將roletype欄位擴展為64位,但在系統的後期迭代階段影響範圍頗大,還是存在用完的時候
2.新增一張表,將複合角色與基礎角色 這兩個拆分位兩個欄位,單獨保存兩者之間關係
四、為什麼in32的範圍是-2^31 ~ 2^31-1 ?
為什麼會介紹這個問題,因為當新增角色時,2^32超出了int32的範圍,但是為什麼int32範圍是-2^31 ~ 2^31-1 ?本著對刨根問底的態度,便追尋了下去。
我們可以先研究下8位二進位的標識範圍為什麼是-2^7~2^7-1
這裡要說下 原碼,反碼,補碼的概念。
原碼
正數的原碼就是它的本身
假設使用一個位元組存儲整數,整數10的原碼是:0000 1010
負數用最高位是1表示負數
假設使用一個位元組存儲整數,整數-10的原碼是:1000 1010
反碼
正數的反碼跟原碼一樣
假設使用一個位元組存儲整數,整數10的反碼是:0000 1010
負數的反碼是負數的原碼按位取反(0變1,1變0),符號位(首位)不變
假設使用一個位元組存儲整數,整數-10的反碼是:1111 0101
補碼
正數的補碼和原碼一樣
假設使用一個位元組存儲整數,整數10的補碼是:0000 1010(這一串是10這個整數在電腦中存儲形式)
負數的補碼是負數的反碼加1
假設使用一個位元組存儲整數,整數-10的補碼是:1111 0110(這一串是-10這個整數在電腦中存儲形式)
在電腦中,為什麼不用原碼和反碼,而是用補碼呢?
使用原碼計算10-10
0000 1010 (10的原碼)
+ 1000 1010 (-10的原碼)
------------------------------------------------------------
1001 0100 (結果為:-20,很顯然按照原碼計算答案是否定的。)
分析:正常的加法規則不適用於正數與負數的加法,因此必須制定兩套運算規則,一套用於正數加正數,還有一套用於正數加負數。從電路上說,就是必須為加法運算做兩種電路
使用反碼計算10-10
0000 1010 (10的反碼)
+ 1111 0101 (-10的反碼)
------------------------------------------------------------
1111 1111 (計算的結果為反碼,我們轉換為原碼的結果為:1000 0000,最終的結果為:-0,很顯然按照反碼計算答案也是否定的。)
使用補碼計算10-10
0000 1010 (10的補碼)
+ 1111 0110 (-10的補碼)
------------------------------------------------------------
1 0000 0000 (由於我們這裡使用了的1個位元組存儲,因此只能存儲8位,最高位(第九位)那個1沒有地方存,就被丟棄了。因此,結果為:0)
分析:補碼表示法可以將加法運算規則,擴展到整個整數集,從而用一套電路就可以實現全部整數的加法。補碼是電腦中存儲整數的形式。
八位二進位正數的補碼範圍是0000 0000 ~ 0111 1111 即0 ~ 127
負數的補碼範圍是正數的原碼0000 0000 ~ 0111 1111 取反加一(也可以理解為負數1000 0000 ~ 1111 1111化為反碼末尾再加一)。 所以得到 1 0000 0000 ~ 1000 0001
1000 0001作為補碼,其反碼是1000 0000,其原碼是1111 1111(-127)
依次往前推,可得到1111 1111作為補碼,其反碼1111 1110,原碼1000 0001(-1)
那麼補碼0000 0000(1被捨去)的原碼是1000 0000符號位同時也可以看做數字位即表示-128(-2^7)
類推:in32的範圍便是-2^31 ~ 2^31-1
五、同餘的概念
兩個整數a,b,若它們除以整數m所得的餘數相等,則稱a,b對於模m同餘
記作 a ≡ b (mod m)
讀作 a 與 b 關於模 m 同餘。
六、模的概念
時間不早了,模的概念可以幫助理解補數和補碼,下篇博客中提到吧。。。
博主的文章沒有高度、深度和廣度,只是湊字數。由於博主的水平不高(其實是個菜B),不足和錯誤之處在所難免,希望大家能夠批評指出。
博主是利用讀書、參考、引用、抄襲、複製和粘貼等多種方式寫的文章,請原諒博主成為一個無恥的文檔搬運工!
參考:
https://www.cnblogs.com/yinzhengjie/p/8666354.html
https://blog.csdn.net/fenzang/article/details/53500852?utm_source=itdadao&utm_medium=referral
http://www.ruanyifeng.com/blog/2009/08/twos_complement.html
http://www.cnblogs.com/zhangziqiu/archive/2011/03/30/ComputerCode.html#!comments



