洛谷P1337 [JSOI2004]平衡點 / 弔打XXX(模擬退火)

題目描述

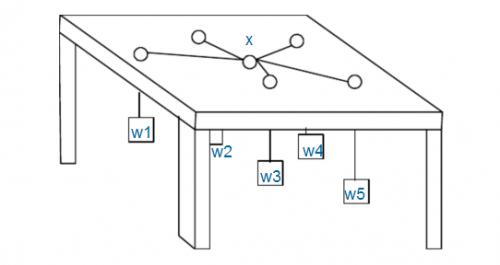
如圖：有n個重物，每個重物系在一條足夠長的繩子上。每條繩子自上而下穿過桌面上的洞，然後系在一起。圖中X處就是公共的繩結。假設繩子是完全彈性的（不會造成能量損失），桌子足夠高（因而重物不會垂到地上），且忽略所有的摩擦。

問繩結X最終平衡於何處。

註意：桌面上的洞都比繩結X小得多，所以即使某個重物特別重，繩結X也不可能穿過桌面上的洞掉下來，最多是卡在某個洞口處。

輸入輸出格式

輸入格式：

文件的第一行為一個正整數n（1≤n≤1000），表示重物和洞的數目。接下來的n行，每行是3個整數：Xi.Yi.Wi，分別表示第i個洞的坐標以及第 i個重物的重量。(-10000≤x,y≤10000, 0<w≤1000 )

輸出格式：

你的程式必須輸出兩個浮點數（保留小數點後三位），分別表示處於最終平衡狀態時繩結X的橫坐標和縱坐標。兩個數以一個空格隔開。

輸入輸出樣例

3
0 0 1
0 2 1
1 1 1

0.577 1.000

說明

[JSOI]

居然是道物理題QWQ...

我們所需要求的點，一定是總能量最小的點，這裡的總能量，就是每個點的重力勢能之和，如果讓一個點的重力勢能減小，那麼拉它的繩子就應該儘量的長，那麼在桌面上的繩子就應該儘量的短

因此我們需要求得一個點，使得$\sum_{1}^{n} d[i]*w[i]$最小（$d[i]$表示該到平衡點的距離，$w[i]$表示該點的重量）

這樣的話我們顯然可以用模擬退火去求這個點

但此題正解並不是模擬退火，

用退火的時候大概有幾個需要註意的地方

1.$\Delta T$要設的大一點，

2.移動的距離需要與溫度有關

然後無腦退火就可以了

親測時間種子用19260817可過

#include<cstdio>
#include<cmath>
#include<ctime>
#include<cstdlib> 
#define Rand(T) T*( (rand()<<1) - RAND_MAX )
const int MAXN = 1e6 + 10;
const double eps = 1e-16;
using namespace std;
inline int read() {
    char c = getchar();int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1;c = getchar();}
    while(c >= '0' && c <= '9') {x = x * 10 + c - '0';c = getchar();}
    return x * f;
}
int N;
struct Point {
    double x, y, w;
}a[MAXN];
double AverX,AverY;
double calc(double x,double y) {
    double ans = 0;
    for(int i = 1; i <= N; i++)
        ans += sqrt((x - a[i].x) * (x - a[i].x) + (y - a[i].y) * (y - a[i].y)) * a[i].w;
    return ans;
}
int main() {
    srand(19260817);
    N = read();
    for(int i = 1; i <= N; i++) 
        scanf("%lf%lf%lf", &a[i].x, &a[i].y, &a[i].w),
        AverX += a[i].x, AverY += a[i].y;
    AverX /= N; AverY /= N;
    double Best = calc(AverX, AverY), BestX = AverX, BestY = AverY;
    double DelatT = 0.98;
    int Time = 10;
    while(Time--) {
        double Now = calc(AverX, AverY), NowX = AverX, NowY = AverY;
        for(double T = 1000000; T > eps; T *= DelatT) {
            double Wx = NowX + Rand(T), Wy = NowY + Rand(T);
            double Will = calc(Wx, Wy);
            if(Will < Best) Best = Will, BestX = Wx, BestY = Wy;
            if(Will < Now || ( exp((Will - Now) / T) * RAND_MAX < rand() ))
                Now = Will, NowX = Wx, NowY = Wy;
        }
    }
    printf("%.3lf %.3lf", BestX, BestY);
    return 0;
}