PageRank之基於C和C#的基本實現

来源:https://www.cnblogs.com/Oliva/archive/2018/04/12/8811314.html
-Advertisement-
Play Games

重點不是說PageRank是什麼，而是怎麼用代碼實現 什麼是PageRank？ PageRank，網頁排名，又稱網頁級別、Google左側排名或佩奇排名，是一種由[1] 根據網頁之間相互的超鏈接計算的技術，而作為網頁排名的要素之一，以Google公司創辦人拉里·佩奇（Larry Page）之姓來命名 ...


重點不是說PageRank是什麼，而是怎麼用代碼實現

什麼是PageRank？

PageRank，網頁排名，又稱網頁級別、Google左側排名或佩奇排名，是一種由[1]  根據網頁之間相互的超鏈接計算的技術，而作為網頁排名的要素之一，以Google公司創辦人拉里·佩奇（Larry Page）之姓來命名。Google用它來體現網頁的相關性和重要性，在搜索引擎優化操作中是經常被用來評估網頁優化的成效因素之一。Google的創始人拉里·佩奇和謝爾蓋·布林於1998年在斯坦福大學發明瞭這項技術。

PageRank的誕生背景?

早期的搜索引擎經歷了“不評價” 和“基於檢索詞”的評價兩個階段。 “基於檢索詞”的評價演算法很直觀，但是容易受到“Term Spam”的攻擊。其實從搜索引擎出現的那天起，spammer和搜索引擎反作弊的鬥法就沒有停止過。Spammer是這樣一群人——試圖通過搜索引擎演算法的漏洞來提高目標頁面（通常是一些廣告頁面或垃圾頁面）的重要性，使目標頁面在搜索結果中排名靠前。用戶很容易被帶入垃圾網頁，用戶體驗極差。PageRank也應運而生。

怎麼實現PageRank?

   簡單的說PageRank讓鏈接來"投票"，一個頁面的“得票數”由所有鏈向它的頁面的重要性來決定，到一個頁面的超鏈接相當於對該頁投一票。一個頁面的PageRank是由所有鏈向它的頁面（“鏈入頁面”）的重要性經過遞歸演算法得到的。一個有較多鏈入的頁面會有較高的等級，相反如果一個頁面沒有任何鏈入頁面，那麼它沒有等級。

最簡單pagerank模型

網頁，可以抽象成的圖當中的結點，網頁與網頁當中的鏈接關係可以模型化為數據結構中邏輯結構圖再具體點是有向圖（表示哪個網頁鏈接哪個網頁），我們可以把鏈接關係用作離散數學圖論當中的可達矩陣形象具體的表示，下麵我來給大傢具體的說明，如下麵這個例子:

 

這個例子中有四個網頁，如果當前在A網頁，那麼上網者將會各有1/3的概率瀏覽到B、C、D網頁，這裡的3表示A有3條出鏈，如果一個網頁有k條出鏈，那麼跳轉任意一個出鏈上的概率是1/k，同理D到B的概率1，而B到C的概率為1。一般用轉移矩陣表示上網者的跳轉概率，如果用n表示網頁的數目，則轉移矩陣M是一個n*n的方陣（可由可達矩陣轉換成轉移矩陣）；如果網頁j有k個出鏈，那麼對每一個出鏈指向的網頁i，有M[i][j]=1/k，而其他網頁的M[i][j]=0；上面示例圖對應的可達矩陣如下：

 
     A   B     C    D

A      0   1     0   0

B      1   0     0   1 

C      1   1     0   0

D      1   0     1   0

對應的轉移矩陣為：

       A      B     C     D

A      0      0.5   0    0

B      0.33   0     0    1 

C      0.33   0.5   0    0

D      0,33   0     1    0        

 

剛開始的時候，假設上網者在每一個網頁的概率都是相等的（這個假設確實存在，假設世界上只有n個網頁，那麼我只能開始的時候進入n個網頁當中的一個，就是1/n），即1/n，於是開始的時候的概率分佈就是一個所有值都為1/n的n維列向量V0（我們以概率分佈向量的結果作為網頁的質量結果，因為質量越高，被上網者瀏覽的概率越大，也稱pr值的大小），在轉移矩陣M去右乘概率分佈向量V0，就得到了第一步之後上網者的概率分佈向量MV0,（nXn）*(nX1)依然得到一個nX1的矩陣。下麵是V1的計算過程：

註意矩陣M中M[i][j]不為0表示用一個鏈接從j指向i，M的第一行乘以V0，表示累加所有網頁到網頁A的概率即得到0.125。得到了V1後，再用V1去右乘M得到V2，一直下去，最終V會收斂，即Vn=MV(n-1)，上面的圖示例，不斷的迭代，最終

V=[0.177,0.319,0.225，0.277]’

(演算法的證明這裡我們就不證明瞭，有興趣的朋友可以百度一下)

終止點問題

上述上網者的行為是一個馬爾科夫過程的實例，要滿足收斂性，需要具備一個條件：

圖是強連通的，即從任意網頁可以到達其他任意網頁.

但是在浩瀚的互聯網中，網頁肯定是不滿足強連通特性的，我們設計模型的時候想要達到強連通特性是很簡單的，但是在互聯網上有一些網頁不指向任何網頁，如果按照上面的計算，當瀏覽到這個沒有指向的網頁的時候那是不是就無法出去了呢？，導致前面累計得到的轉移概率被清零，這樣下去，最終的得到的概率分佈向量所有元素幾乎都為0。假設我們把上面圖中B到A的鏈接丟掉，A變成了一個終止點，得到下麵這個圖：

 

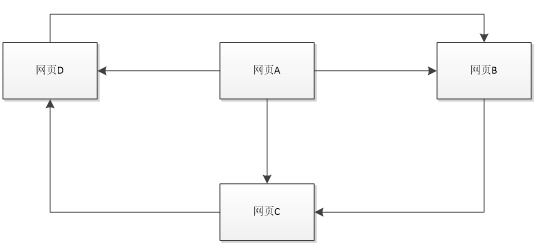
對應的轉移矩陣為：

       A      B     C   D

A      0      0     0   0

B      0.33   0     0   1 

C      0.33   1     0   0

D            0.33      0           1       0          

 

連續迭代下去，最終所有元素都為0。

 

陷阱問題

要是有投機取巧這想到用網頁自己鏈接自己，讓我們瀏覽這中了這個無線迴圈的陷阱怎麼辦呢？：

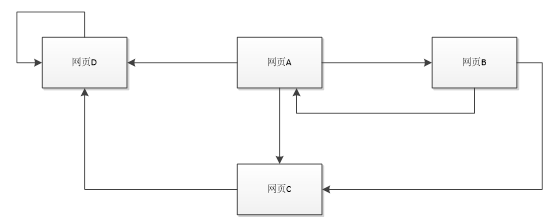
上網者跑到D網頁後，再也不能從D中出來，將最終導致概率分佈值全部轉移到D上來，這使得其他網頁的概率分佈值為0，從而整個網頁排名就失去了意義。如果按照上面圖對應的轉移矩陣為：

        A     B     C    D

A       0     0.5   0    0

B      0.33   0     0    0

C      0.33   0.5   0    0

D      0,33    0    1    1        

 

不斷的迭代下去，的結果一定會是[0,0,0,1]的

 

解決終止點問題和陷阱問題

 

其實會出現這兩個問題，是因為最開始構建模型的時候我們忽略了一個東西：上網者可以隨時跳出他瀏覽的網頁（瀏覽器上輸入網址就行了），而不需要擔心，要是瀏覽的網頁沒有鏈接那不就是不能出去了嗎？（結果只需要輸入網址就可以跳出去），那瀏覽的網頁連接了自己瀏覽這不就一直在瀏覽這個了嗎？（結果是瀏覽者發現這是陷阱都在重覆瀏覽一個網頁的時候，他可以輕鬆跳過去，只需要輸入網址即可），當然正常情況他也是可以輸入網址跳轉任何他想去的網頁，這個時候我們需要引入一個概念：阻尼繫數（簡單來說就是點擊網頁的概率-實際上就是用戶感到無聊，停止點擊，隨機跳到新URL的概率），這裡我們取α = 0.8，當然也有很多的覺得0.85是好的，這個概念已經給出，數值看我們自己~（覺得能讓你的結果符合預期就ok啦..）。 從而我們得到了更加完善的公式：

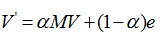
由於這些是數學上的計算，有了公式是比較容易推出結果來的，所以就不在舉例啦~~

 

如何通過代碼具體的實現?

 

   可以把每個網頁所構成的複雜的關係模型化成數據結構的邏輯結構圖(有向圖)，每個網頁就是一個結點，當一個網頁(網頁A)鏈接著另一個網頁(網頁B)的時候可以抽象的看出A->B,即通過出度和入度來描述鏈接和被鏈接數，當你通過創建有向圖的時候其實就相當於模擬了網頁之間的關係(當然浩瀚的互聯網中網頁數不勝數,我這裡只是通過一個小的環境模擬這個演算法的實現),通過PageRank演算法加之迭代，使其每個網頁的pr(衡量網頁質量的參數)值都趨於穩定的時候,由pr值大小排序出來的網頁的先後順序可以相對準確的衡量網頁質量。

 

       我先是通過c語言模型化PageRank的演算法 算出每個結點(網頁)的pr值。

 

      

 

需要構建有向圖來模型化網頁（c語言的結點是手動輸入的，因為為了測試方便嘛~）

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

#define OK 1
#define ERROR -1
#define FALSE 0
#define TRUE 1
#define MAXVER 20  //定義最大頂點數
#define MAXQSIZE 100
//#define OVERFLOW -2

typedef char verType;    //頂點類型
typedef int Status;
typedef int Boolean;

typedef struct
{
    verType verx[MAXVER];
    int arcs[MAXVER][MAXVER];    //鄰接矩陣
    int vernum, arcnum;    //定義最大頂點數 和 弧
}MGraph;

Boolean visited[MAXVER];    //頂點開始都沒有被訪問過
int locate(MGraph G, verType ch);    //查找頂點在數組中的下標
Status CreateDG(MGraph *G,int v);    //創建有向圖
void Create_Transfer_matrix(MGraph G, double ***F);    //創建轉移矩陣
double** Mat_mul(double **M1, int num);    //矩陣相乘
int GetNum(MGraph G, int h, int l);    //得到每一行非0項的個數
double *Iteration(double *M1, double **M2, double *M, int num);    //迭代法
int main(void)
{
    double **F = NULL;
    MGraph G;
    CreateDG(&G, 0);
    Create_Transfer_matrix(G, &F);
    Mat_mul(F, G.vernum);
    return 0;
}


double *Iteration(double *M1, double **M2, double *M, int num)
{//迭代法
    double *M3, temp = 0;
    int i, j;
    M3 = malloc(num * sizeof(double));
    printf("\n");
    for(i = 0; i < num; i++)
    {
        printf("@ = %0.10lf\n", M[i]);
    }
    for (i = 0; i < num; i++)
    {
        for (j = 0; j < num; j++)
        {
            temp = M1[j] * M2[i][j] + temp;
        }
        M3[i] = temp + M[i];
        temp = 0;
    }
    putchar(10);
    for (i = 0; i < num; i++)
    {
        printf("%.10lf\n", M3[i]);
    }
    putchar(10);

    return M3;
}

double** Mat_mul(double **M1, int num)
{
    int i,j;
    double *M2, *M3, temp = 0, *M;
    M3 = malloc(num *sizeof(double));
    M2 = malloc(num * sizeof(double));
    for (i = 0; i < num; i++)        //初始化概率分佈矩陣
    {
        M2[i] = (1.0 / num * 1.0);
    }
    for (i = 0; i < num; i++)
    {
        for (j = 0; j < num; j++) 
        {
            temp = M1[i][j] * M2[j] + temp;
        }
        M3[i] = temp + M2[i] * 0.2;
        temp = 0;
    }
    for (i = 0; i < num; i++)
    {
        printf("%.10lf\n", M3[i]);
    }
    for (j = 0; j < num; j++) 
    {
        M2[j] = M2[j] * 0.2;
    }
    M = Iteration(M3, M1, M2, num);    //調用函數實現轉移矩陣和概率向量的相乘
    while (fabs(M[0] - M3[0]) > 0.0000000001)    //設置迭代結束條件
    {
        M3 = M;
        M = Iteration(M3, M1, M2, num);
        
    }    
    for (i = 0; i < num; i++)
    {
        M[i] = M[i] * 0.8 + 0.2 / num;
    }
    for (i = 0; i < num; i++)
        printf(" - %.10lf\n", M3[i] - 0.0000000001);
    return M1;
    
}

void Create_Transfer_matrix(MGraph G, double ***F)
{//創建轉移矩陣
    int i, j;
    (*F) = malloc(G.vernum * sizeof(double *));
    for (i = 0; i < G.vernum; i++)
    {
        (*F)[i] = malloc(G.vernum * sizeof(double));
    }
    for (i = 0; i < G.vernum; i++)
    {
        for (j = 0; j < G.vernum; j++)
        {
            if (GetNum(G, G.vernum, i) == 0)
                (*F)[j][i] = 0;
            else
                (*F)[j][i] = 0.8 * (G.arcs[j][i] / (GetNum(G, G.vernum, i) * 1.0));
        }
    }
    putchar(10);
    printf("\n轉移矩陣為:\n");
    for (i = 0; i < G.vernum; i++)
    {
        for (j = 0; j < G.vernum; j++)
        {
            printf("%.10lf ", (*F)[i][j]);
        }
        printf("\n");
    }
    printf("\n");
}

int locate(MGraph G, verType ch)
{
    int i;
    for (i = 0; i < G.vernum && ch != G.verx[i]; i++);
    return i;

}

Status CreateDG(MGraph *G,int v)
{
    int i, j, k;
    verType ch1, ch2;
    printf("請輸入有向圖的頂點數和弧數,格式如(0 0): ");
    scanf("%d %d", &G->vernum, &G->arcnum);
    fflush(stdin);    //除緩存
    printf("請輸入頂點符號:\n");
    for (i = 0; i < G->vernum; i++)
    {
        scanf("%c", &G->verx[i]);
        fflush(stdin);
    }
    for (i = 0; i < G->vernum; i++)
    {
        for (j = 0; j < G->vernum; j++)
        {
            G->arcs[i][j] = 0;    //賦初值
        }
    }
    printf("請輸入有連接的點: 格式(A B)\n");
    for (i = 0; i < G->arcnum; i++)
    {
        printf("請輸入第%d對值\n", i + 1);
        scanf("%c %c", &ch1, &ch2);    //輸入頂點符號
        fflush(stdin);
        k = locate(*G, ch1);   //獲得頂點下標
        j = locate(*G, ch2);
        G->arcs[j][k] = 1;  //為鄰接矩陣賦值
    }
    return OK;
}

int GetNum(MGraph G, int h, int l)    //得到每一列非0的個數
{
    int i, Num = 0;
    for (i = 0; i < h; i++)
    {
        if (G.arcs[i][l] > 0)
        {
            Num++;
        }
    }
    return Num;
}

雖然實現了PageRank的演算法但是僅僅是實現了而且，想要有趣一點的話可以簡單模擬一下PageRank的應用背景:我在一個文件夾下麵建立的多個HTML的網頁(相互之間有鏈接),通過PageRank演算法把每個網頁的質量進行了排名，由程式給出排名順序反饋給用戶（通過C#實現的）

 

這個是提前創好的簡單的HTML網頁(我的目的是模擬，所有網頁只有一個標簽，有的連標簽都沒有……)

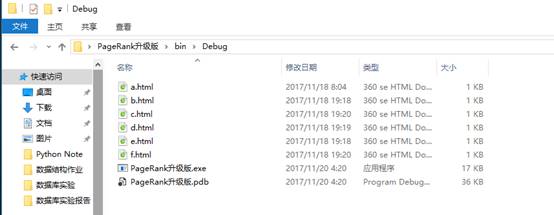
大家可以看出a是被鏈接最多的網頁，其他的被鏈接的先後順序相信大家也可以看出來，下麵開始演示程式:

1.首先輸入網頁所在的文件夾：

 

2.通過配置計算環境及其其他的相關事宜:

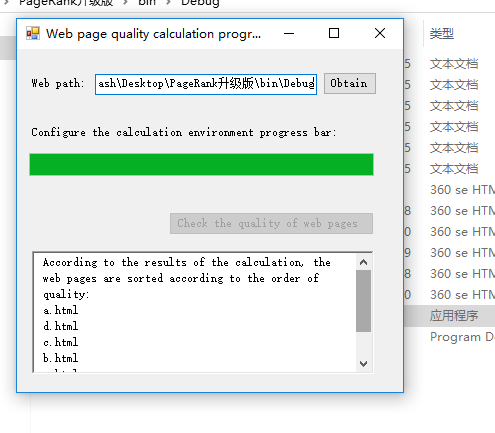
3.獲得網頁質量:

通過程式的排序已經將質量相當大小反饋給用戶,用戶可以選擇性的瀏覽網頁

我們用C語言的來驗證每個網頁的pr值是否真如此程式所言

(註意 – 是一個標誌，表示最終迭代的結果…) 由上到下依次為A~F的pr值，正如C#的程式排序所言，證明這個是合理的

 

 

------由於c#的代碼不是一兩張圖片就可以解釋的清楚的，所有有興趣的朋友可以一起探討和分享。

（這個程式是我才學習了C#寫的，如果有什麼不足或者錯誤之處請多多包涵）

 

需要源碼的朋友可以評論區或者私信我留下你們的郵件，我看到後會儘快發給你們源碼滴，大家一起進步一起學習

 


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • React--組件
    註意 /`會報錯 React的props React中的每一個組件，都包含有一個屬性（props），在組件內部，我們可以通過this.props獲取屬性對象。 組件如下： 屬性使用方法： 1.直接調key/value 2.延展屬性 用{...props}方法 3.調用組件的setProps函數來指定 ...
  • Java 微服務框架選型（Dubbo 和 Spring Cloud？）
    微服務（Microservices）是一種架構風格，一個大型複雜軟體應用由一個或多個微服務組成。系統中的各個微服務可被獨立部署，各個微服務之間是松耦合的。每個微服務僅關註於完成一件任務並很好地完成該任務。在所有情況下，每個任務代表著一個小的業務能力。 以往我們開發應用程式都是單體型（可以看作是一個怪 ...
  • 設計模式之備忘錄模式（Memento ）
    當我們在實際應用中需要提供撤銷機制，當一個對象可能需要再後續操作中恢復其內部狀態時，就需要使用備忘錄模式。其本質就是對象的序列化和反序列化的過程，支持回滾操作。 作用 在不破壞封裝性的前提下，捕獲一個對象的內部狀態，併在該對象之外保存這個狀態，這樣以後就可以將該對象恢復到原先的狀態。 類視圖 實現 ...
  • C#設計模式——簡單工廠模式、工廠模式和抽象工廠模式
    一：簡單工廠模式 1：描述：簡單工廠模式是由一個工廠對象根據接收到的消息決定要創建哪一個類的對象事例。 2：優點：工廠類中有相關邏輯判斷，可以根據需要動態創建相關的對象事例，而客戶端只需要告訴工廠類創建什麼對象事例，而不關心怎麼創建，當需要引入新產品就不需要修改客戶端的代碼，只需要添加相應的產品類並 ...
  • 關於hibernate的核心配置
    一、hibernate中的核心配置文件：hibernate.rfg.xml 對於hibernate的核心配置文件有兩種：1.hibernate.rfg.xml，2.hibernate.properties。開發中我們最常用的是hibernate.rfg.xml的配置文件，因為它的配置能力強，易於修改 ...
  • 初學Java Web(8)——過濾器和監聽器
    什麼是過濾器 過濾器就是 Servlet 的高級特性之一， 就是一個具有 攔截/過濾 功能的一個東西，在生活中過濾器可以是香煙濾嘴，濾紙，凈水器，空氣凈化器等，在 Web 中僅僅是一個 實現了 Filter 介面的 Java 類 而已。 特點：雙向，攔截請求，攔截響應 作用： 過濾器可以對 所有的請 ...
  • 利用for迴圈如何判定是水仙花數
    水仙花數業內的大家可能聽說過，但是對於初學者來講，對於水仙花數還是比較陌生的。 首先要知道的是水仙花數的計算公式：153=1**3+5**3+3**3： 如何去判定這個數是否為水仙花數，最好的辦法就是用for內嵌迴圈了，因為涉及到了公式所以很多數學邏輯不是很好的兄臺，就尷尬了，其實有一個比較簡單的數 ...
  • Java筆記 —— 初始化
    閱讀目錄 屬性初始化和構造器調用 初始化的順序 靜態塊和非靜態塊 初始化的方式 數組初始化 閱讀目錄 閱讀目錄 屬性初始化和構造器調用 初始化的順序 靜態塊和非靜態塊 初始化的方式 數組初始化 屬性初始化和構造器調用 初始化的順序 靜態塊和非靜態塊 初始化的方式 數組初始化 一、屬性初始化和構造器調 ...
一周排行
    -Advertisement-
    Play Games
  • WPF 已知問題 監聽 WMI 事件導致觸摸失效
    示例項目結構 在 Visual Studio 中創建一個 WinForms 應用程式後，項目結構如下所示： MyWinFormsApp/ │ ├───Properties/ │ └───Settings.settings │ ├───bin/ │ ├───Debug/ │ └───Release/ ...
  • [STAThread]特性
    [STAThread] 特性用於需要與 COM 組件交互的應用程式，尤其是依賴單線程模型（如 Windows Forms 應用程式）的組件。在 STA 模式下，線程擁有自己的消息迴圈，這對於處理用戶界面和某些 COM 組件是必要的。 [STAThread] static void Main(stri ...
  • UWP WinUI3 傳入 AddHandler 的 RoutedEventHandler 類型與事件所需不匹配將拋出參數異常
    在WinForm中使用全局異常捕獲處理 在WinForm應用程式中，全局異常捕獲是確保程式穩定性的關鍵。通過在Program類的Main方法中設置全局異常處理，可以有效地捕獲並處理未預見的異常，從而避免程式崩潰。 註冊全局異常事件 [STAThread] static void Main() { / ...
  • .NET 多版本 WinForm 開源控制項庫 SunnyUI
    前言 給大家推薦一款開源的 Winform 控制項庫，可以幫助我們開發更加美觀、漂亮的 WinForm 界面。 項目介紹 SunnyUI.NET 是一個基於 .NET Framework 4.0+、.NET 6、.NET 7 和 .NET 8 的 WinForm 開源控制項庫，同時也提供了工具類庫、擴展 ...
  • .net core8 使用Swagger（附當前源碼）
    說明 該文章是屬於OverallAuth2.0系列文章，每周更新一篇該系列文章（從0到1完成系統開發）。 該系統文章，我會儘量說的非常詳細，做到不管新手、老手都能看懂。 說明：OverallAuth2.0 是一個簡單、易懂、功能強大的許可權+可視化流程管理系統。 有興趣的朋友，請關註我吧(*^▽^*) ...
  • WPF 什麼時候 VisualTreeHelper.GetDescendantBounds 將返回無窮大
    一、下載安裝 1.下載git 必須先下載並安裝git，再TortoiseGit下載安裝 git安裝參考教程：https://blog.csdn.net/mukes/article/details/115693833 2.TortoiseGit下載與安裝 TortoiseGit，Git客戶端，32/6 ...
  • C# 開源教程帶你輕鬆掌握數據結構與演算法
    前言 在項目開發過程中，理解數據結構和演算法如同掌握蓋房子的秘訣。演算法不僅能幫助我們編寫高效、優質的代碼，還能解決項目中遇到的各種難題。 給大家推薦一個支持C#的開源免費、新手友好的數據結構與演算法入門教程：Hello演算法。 項目介紹 《Hello Algo》是一本開源免費、新手友好的數據結構與演算法入門 ...
  • 第22篇 生成proto文件bat腳本
    1.生成單個Proto.bat內容 @rem Copyright 2016, Google Inc. @rem All rights reserved. @rem @rem Redistribution and use in source and binary forms, with or with ...
  • 記一次 .NET某上位機視覺程式 卡死分析
    一：背景 1. 講故事 前段時間有位朋友找到我，說他的窗體程式在客戶這邊出現了卡死，讓我幫忙看下怎麼回事？dump也生成了，既然有dump了那就上 windbg 分析吧。 二：WinDbg 分析 1. 為什麼會卡死 窗體程式的卡死，入口門檻很低，後續往下分析就不一定了，不管怎麼說先用 !clrsta ...
  • 醫學DICOM文件與PACS系統進行數據傳輸
    前言 人工智慧時代，人臉識別技術已成為安全驗證、身份識別和用戶交互的關鍵工具。 給大家推薦一款.NET 開源提供了強大的人臉識別 API，工具不僅易於集成，還具備高效處理能力。 本文將介紹一款如何利用這些API，為我們的項目添加智能識別的亮點。 項目介紹 GitHub 上擁有 1.2k 星標的 C# ...
所有分類