linux下平衡二叉樹以樹形列印來描述插入、刪除的流程

来源:https://www.cnblogs.com/lan-keke/archive/2018/03/25/8631809.html
-Advertisement-
Play Games

這篇文章主要是為了溫習下平衡二叉樹，同時添加了樹型列印的介面，讓平衡二叉樹的添加和刪除更容易理解。 接下來的篇幅很長，需要有很多的耐心，做好了準備接下來往下看吧。 通俗的來說： 二叉樹就是節點度最大為2的樹，也就是最多包含兩個子樹，左子樹和右子樹，包含了空樹。 二叉排序樹(Binary Sort T ...


這篇文章主要是為了溫習下平衡二叉樹，同時添加了樹型列印的介面，讓平衡二叉樹的添加和刪除更容易理解。

接下來的篇幅很長，需要有很多的耐心，做好了準備接下來往下看吧。

通俗的來說：

二叉樹就是節點度最大為2的樹，也就是最多包含兩個子樹，左子樹和右子樹，包含了空樹。

二叉排序樹(Binary Sort Tree)是在二叉樹的基礎上進行了規整，滿足以下規則：

　　　　1）節點的值是能夠進行大小比較的。

　　　　2）如果節點的左子樹不為空，則左子樹上的節點都比該節點小。

　　　　3）如果節點的右子樹不為空，則右子樹上的節點都比該節點大。

　　　　4）節點的左、右子樹同時也是二叉排序樹。

 

看完規則，那滿足二叉排序樹的樹有很多，如下列圖：

　　                

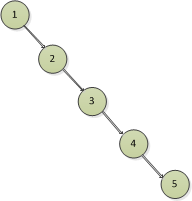
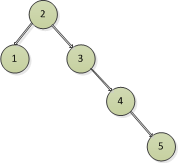
　　　　　圖1　　　　　　　　　　　　　    圖2

                   

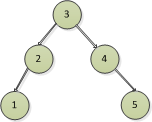
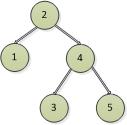
　　　     圖3                                                 圖4

上面的圖都滿足二叉排序樹，左邊的節點都比右邊的節點小，我們知道二分查找的最好時間複雜度為O(log2n)，而二叉排序樹的查找類似於二分查找，要麼找左邊，要麼找右邊。

在上述的圖中，圖1中如果要尋找節點5，則必須將整個樹全部遍歷一遍，才能比較找到5這個節點，圖2花的步數會少一些，圖3和圖4就花費的步數就更少了。

所以為了讓二叉排序樹也能像二分查找一樣，保持接近於最好的時間複雜度O(log2n)，則二叉排序樹的深度越少越好，這樣就有了平衡二叉樹(AVL)。

 

平衡二叉樹其實就是所有節點的左右子樹高度相差不超過1的二叉排序樹，包含空樹。

所以平衡二叉樹是要滿足二叉排序樹的規則的，所以平衡二叉樹只是二叉排序樹的一個約定的特例，就比如皇帝柑之於柑橘，只是好吃了一點而已。

左右子樹的高度差都不超過1，沒有要求是左邊高還是右邊高，那就存在以下三種情況：

　　　　註：（有的以高度為0開始，這裡高度以1開始，也就是空節點高度為0，一個節點的高度為1）

　　　　如果一樣高則高度一致，所以高度差為0;

　　　　如果左邊高則左邊比右邊高，滿足平衡二叉樹高度不超過1，我們把高度差記為1（左子樹高度減去右子樹高度）;

              如果右邊高則右邊比左邊高，滿足平衡二叉樹高度不超過1，我們把高度差記為-1（左子樹高度減去右子樹高度）;

       這就是平衡因數的概念，平衡因數是相對於每一個節點而言的，概括就是左高減右高，如果要求出平衡因數，那麼肯定是某個節點的平衡因數，求解得出來的平衡因數也是相對

某一個節點而言的。接下來我們討論下這三種情況，並且解釋下平衡因數的標識，以下三種情況以高度差來表示平衡因數。

　　1）兩邊一樣高，也就是高度差為0，如下圖

　　　     　                            

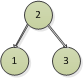
　　　　　　圖5                            圖6

               在圖5和圖6中，

　　　　首先看下圖5，單個節點構成一棵二叉樹，只有根節點，根節點沒有左節點和右節點，所以圖5中節點高度差為0。記錄為下圖

　　　　

 

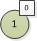
　　　　再看圖6，首先根節點有了兩個子節點，也可以稱為子樹。首先1節點和3節點屬於葉子節點(樹上度為0的節點，沒有左右子樹，長得和圖5中的節點很像)，

　　   所以1節點和3節點的高度差為0。

　　　　

 

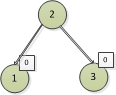
　　　　再來看2節點，2節點左邊有一個1節點，所以左邊的高度為1,同理，右邊的3節點的高度也為1，高度差為兩邊

          高度差，1-1=0。

　　　　

 

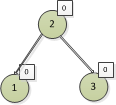
　　2）左邊高，也就是左邊的高度比右邊高1，如下圖

                                  

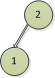
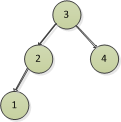
                    圖7                                 圖8

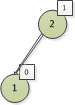
　　　　   先看圖7，圖中有兩個節點，1節點屬於葉子節點，沒有左右子樹，1節點的高度差為0，然後看2節點，2節點左邊有一個1節點，左邊高度為1，

　　　　右邊是沒有節點的，高度為0，所以高度差為1-0=1。

　　　　

 

　　　　在圖7的基礎上補上節點3和4形成圖8，節點1和4屬於葉子節點，高度差為0, 2節點高度差為1，我們先標上已知的高度差

　　　　

 

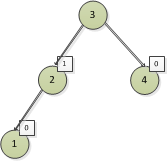
　　　　然後看下3節點，左邊子樹包含了1節點和2節點，高度為2，右邊只有一個4節點，高度為1，所以高度差為2-1=1，所以圖中

　　　　節點2和節點3的左子樹都比右子樹高1。

              

　　3）右邊高，也就是右邊的高度比左邊高1，但是按照平衡因數計算方法，左高減右高，所以高度差是-1，如下圖

                               

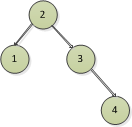
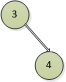
                        圖9                                       圖10

　　　　　在圖9中，我們根據前面查看的示例，可以發現右邊肯定是比左邊高的，還是來標高度差，首先1節點和4節點不用說了

　　　　屬於葉子節點，所以1節點和4節點的高度差為0，還要補充的是，我們查看高度差，採取從我們理解的下到上來標識，先葉子節點，

　　　　然後逐層上升。

　　　　

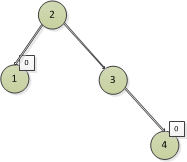
　　　　　然後3節點的高度，左邊高度為0，右邊有一個4節點，所以高度差為0-1=-1，同理2節點的左邊子樹高度為1，右邊高度為2，所以

　　　　高度差為1-2=-1。

               

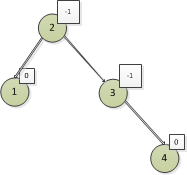
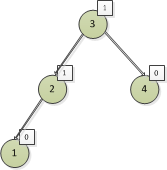
　　　　討論完這三種情況，我們找一個平衡二叉樹來標識平衡因數，下麵還是按照平衡因數來說，我們來標識圖11的平衡因數

　　　           　

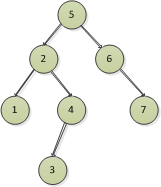
                                      圖11

　　　　　標完的圖如下：

                        

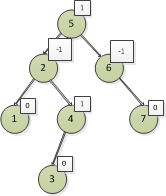
                     可能-1的標識不是很清晰，看框的大小吧，-1的框比1的框要大一些的。

 

說完平衡因數，接下來說下二叉排序樹，為什麼說這個呢，因為平衡二叉樹也是屬於二叉排序樹，只是對高度做了限制，所以平衡二叉樹的添加和刪除都是和二叉排序樹一樣的

只是當添加和刪除了節點之後，還是二叉排序樹，但是可能不滿足平衡二叉樹的要求，所以就會有後續的旋轉啥的。先說二叉排序樹的添加和刪除，以添加起頭。

 

二叉排序樹添加節點

首先最先加入的節點肯定是根節點，我們以上面的圖11為例，我們插入的順序定為{5,2,1,4,3,6,7}，先插入5節點，

插入2節點，先和5進行比較，按照二叉排序樹的要求，比節點小，就往左走，比節點大，就往右走，那麼和節點一樣大呢

那就不要了，不加入二叉排序樹了。因為2比5小，所以往左找，發現沒有左節點，2節點就作為5的左節點。

 

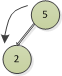
插入1節點，比5小，往左，比2小，再往左，沒找到節點就添加

 

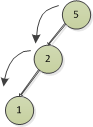
插入4節點，比5小，往左走，比2大，往右走，沒找到節點就添加

 

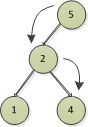
插入3節點，比5小，往左走，比2大，往右走，比4小，往左走，沒找到節點就添加

 

插入6節點，比5大，往右走，沒找到節點就添加

 

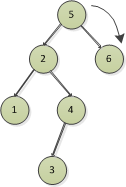
插入7節點，比5大，往右走，比6大，往右走，沒找到節點就添加

 

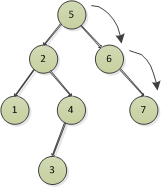
這樣就和圖11是一致的了，如果我們在圖11的基礎上再加入一些節點來說明有相同節點如何處理。那麼插入隊列就改成

{5,2,1,4,3,6,7,9,8,7}，加入了後面的9,8,7三個節點，先插入9和8.

              

 

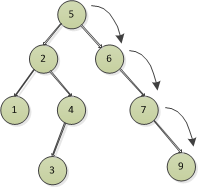
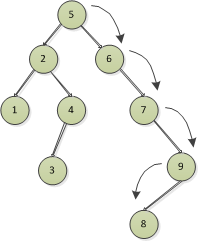
然後插入7節點，比5大，往右走，比6大，往右走，發現和已存的節點7相等，取消插入，直接丟棄。

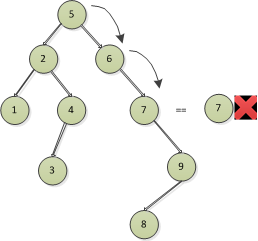
所以最後的二叉排序樹是

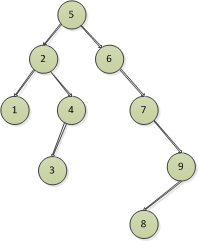
　　　　　圖12

 

二叉排序樹添加的代碼

首先二叉樹的節點的定義如下：

 1）結構體定義

typedef struct _BiTree
{
    int node_data;//節點值

    int bf;//平衡因數

    struct _BiTree *left;//左子樹指針
    struct _BiTree *right;//右子樹指針
    _BiTree(int data)
        : node_data(data), bf(0), left(nullptr), right(nullptr)
    {}
}BiTreeType, *BiTreeTypePtr;

2）二叉排序樹插入節點

　　我們回想之前的插入節點的邏輯：如果樹為空，則添加節點為根節點，不為空，則查找後續節點，如果比查找節點小往左找，如果比查找節點大則往右，

　　如果存在查找節點等於預插入的節點，則丟棄預插入的節店，如果不存在，直到找到樹的最下麵，也就是最後找到nullptr，則插入節點。

　   插入的代碼按照之前畫的圖的思路，

　　1）先判斷是不是空樹，空樹直接添加，

　　2）如果不是空樹，則要找到合適位置，如果節點存在，則不添加，

　　3）反之節點不存在，接著往下找，每一次查找，小於查找節點往左找，大於查找節點往右找，最後添加節點。

bool InsertNode(BiTreeTypePtr &bi_tree, int data)
{
    /*根節點*/
    if (bi_tree == nullptr)
    {
        BiTreeTypePtr node = new BiTreeType(data);
        bi_tree = node;
        return true;
    }
    
    /*在已存的二叉樹中查找節點，如果不存在，就找到合適的位置加入節點*/
    BiTreeTypePtr p = nullptr;
    if (!SearchBBST(bi_tree, data, nullptr, p))
    {
        BiTreeTypePtr node = new BiTreeType(data);
        if (p->node_data > data)
        {
            p->left = node;
        }
        else
        {
            p->right = node;
        }
            
        return true;
    }

    return false;
}

 

 搜索的代碼如下：小往左，大往右，找到nullptr表示走到頭

bool SearchBBST(BiTreeTypePtr bi_tree, int data, BiTreeTypePtr parent, BiTreeTypePtr &choose_node)
{
    /*找到了最後為空的位置，沒有找到節點，記錄父節點，方便添加*/    
    if (nullptr == bi_tree)
    {
        choose_node = parent;
        return false;
    }        
    else if (bi_tree->node_data == data)
    {
        choose_node = bi_tree;
        return true;
    }
    else if (bi_tree->node_data > data)
    {
        return SearchBBST(bi_tree->left, data, bi_tree, choose_node);
    }
    else
    {
        return SearchBBST(bi_tree->right, data, bi_tree, choose_node);
    }
}

 

二叉排序樹刪除節點

插入節點就是在二叉樹中找到對應的位置就添加節點，如果節點存在就丟棄節點，插入成功的節點都是葉子節點。接下來是刪除節點，刪除節點和插入不一樣，

刪除的節點可能是葉子節點，也有可能不是葉節點，存在左子樹或者右子樹，又或者兩者都有，這樣刪除節點之後，子樹必須接上來，繼續組成一個二叉排序樹。

當然如果節點不存在，找不到就沒得刪了。

接下來說刪除節點的4個情況：以圖12為例

　　　　1）刪除的是葉子節點

　　　　　　比如刪除的是1、3、8節點，這幾個節點是沒有子樹的，以刪除8節點為例

　　　　　　    

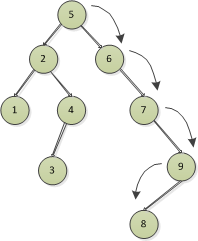
　　　　　　找到8節點，刪除

　　　　　　            

 

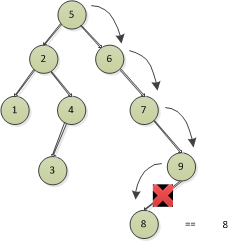
　　　　2）刪除的節點存在左節點，沒有右節點

　　　　　　比如刪除4節點，4節點存在左邊的3節點，右邊是空的

　　　　　　                  

　　　　　　

 

 

　　　　               

 

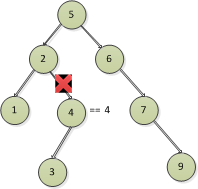
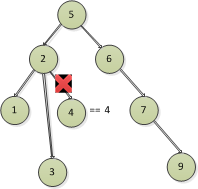
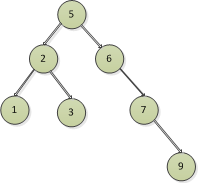
　　　　3）刪除的節點存在右節點，沒有左節點

　　　　　　比如刪除6，7節點，6節點存在右邊的7節點 ，  7節點存在右邊的9節點，而左邊是空的

　　　　　　以刪除7節點為例

　　　　　　                            

 

　　　　　　       

 

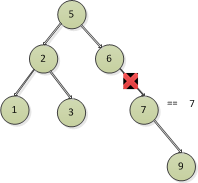
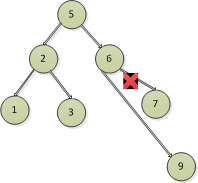
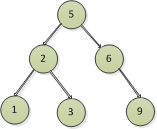
 　　　　所以前三種情況中，刪除節點之後，都是讓節點的左節點或者右節點節點頂上來，葉子節點也是如此，可以認為葉子節點的左右節點

　　　　為空，刪除葉子之後，空給了葉子節點的父節點。這時候父節點也變成了葉子節點

　　　　　　

　　　　4）刪除的節點存在左節點和右節點

　　　　　　比如刪除2節點，2節點存在左邊的1節點和右邊的3節點，同時存在左子樹和右子樹的節點刪除的時候，會跟前三種情況不一樣，

　　　　原則是這樣的，如果刪除的節點同時存在左子樹和右子樹，則讓該節點的前繼節點或者後繼節點來代替該節點，然後刪除前繼節點或者

　　　　後繼節點，前繼節點：數值比刪除節點小並且大小最接近刪除節點的值，後繼節點：數值比刪除節點大並且大小最接近刪除節點的值。

　　　　這裡以後繼節點來演示，首先看如何找後繼節點，因為找後繼節點，所以是要比節點大，那就往右走，再要找到大小最接近刪除節點的值，

              那就是找右邊最小的值。找小的值就往左邊找。

　　　　那找後繼就是往右邊找最左邊的值。

　　　　那找上圖2節點的後繼節點先往右，找到了3節點，再往左，發現沒有節點了，所以3就是要找的節點

　　　　

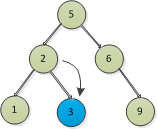
　　　　這種情況是在3節點之後沒有節點了，那再以其他情況解析下

　　　　

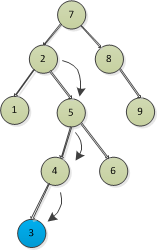
　　　　　　圖13

 　　比如刪除圖13中的2節點，先往右找到5，然後往左找，一直找，會找到最左邊的3節點

　　找到了後繼節點，則刪除有左子樹和右子樹的節點的如下圖：

　　          

　　            

 

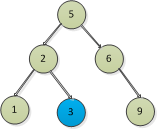
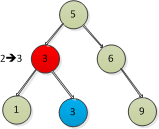
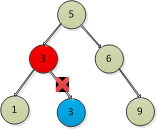
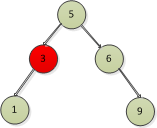
 複雜一點的就是：

                      

 

                

 

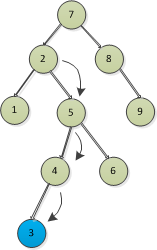
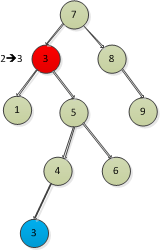
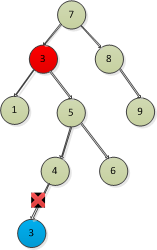
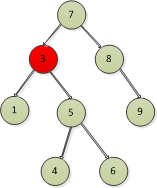
二叉排序樹刪除節點的代碼

　  刪除節點需要分4種情況，但是刪除葉子節點的情況，跟只有左子樹或者右子樹的邏輯一致，可以按照後者來理解，也就是刪除葉子節點的時候

     將葉子節點的左子樹或者右子樹給父節點，反正最後都會成為nullptr。

　　1）首先要找到刪除的節點，找不到都是扯淡，找節點跟添加時候的搜索是一樣的，都滿足一樣的規則，小往左，大往右

　　2）判斷左子樹是否為空，如果為空，標記父節點，將指向父節點的指針指向右子樹，這時候可以想象，如果右子樹為空，相當於刪除的是葉子節點

　　　如果右子樹不為空，則就是上面圖中右子樹頂上來的情況

/*左為空，刪除父節點，右頂上*/
BiTreeTypePtr tmp;
if (nullptr == bi_tree->left)
{
    tmp = bi_tree;
    bi_tree = bi_tree->right;
    delete tmp;
    tmp = nullptr;
}

　　3）同理，右邊的處理和左邊一致，右邊為空，左邊不為空

/*右為空，刪除父節點，左頂上*/
BiTreeTypePtr tmp;
if (nullptr == bi_tree->right)
{
    tmp = bi_tree;
    bi_tree = bi_tree->left;
    delete tmp;
　　 tmp = nullptr;
}

　　4）左子樹和右子樹都不為空的情況：找後繼，右邊找最小的值。後繼節點替換刪除節點，刪除後繼節點

/*先往右找大的節點*/
BiTreeTypePtr p = bi_tree->right;
BiTreeTypePtr tmp = p;
/*往左找最接近的值，後繼值*/
while (nullptr != p->left)
{
    tmp = p;
    p = p->left;
}

/*後繼節點的值給刪除節點，然後後繼節點的父節點左子樹指向後繼節點的右子樹*/
bi_tree->node_data = p->node_data;
tmp->left = p->right;
delete p;
p = nullptr；

其中有一句tmp->left = p->right;

這句的意思是後繼節點的父節點指向後繼節點的右子樹，因為在此刻後繼節點是找到的最左邊的值，

是肯定沒有左子樹的，但是可能有右子樹，這時候刪除後繼節點，右子樹得接上父節點。

所以上面while中tmp = p;就是在保存後繼節點的父節點。

在前面的圖中

      

上兩圖都是沒有右子樹的，加上代碼中是找到最左邊的值，所以後繼節點是沒有左子樹的，所以這種情況就相當於節點的子樹都沒有，等同於葉子節點，刪了就直接刪了

但是如果有右子樹的情況呢，我們加上一個3.5的點，在3節點替換了刪除節點，刪除3節點，那麼3.5節點就需要接上3的父節點，不然後面的

數據就全丟了，因為後面的節點是屬於3的節點，不管多大，都應該是比3的父節點小的，所以後面的所有節點都應該放在4的左子樹上。

        

 

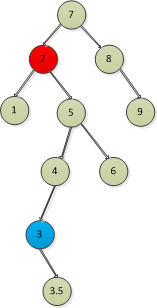
刪除的代碼總結起來如下：

bool DeleteNode(BiTreeTypePtr &bi_tree, int data)
{
    if (nullptr == bi_tree)
    {
        return false;
    }
    else if (bi_tree->node_data > data)
    {
        return DeleteNode(bi_tree->left, data);
    }
    else if (bi_tree->node_data < data)
    {
        return DeleteNode(bi_tree->right, data);
    }
    else
    {
        /*左為空，刪除父節點，右頂上*/
        BiTreeTypePtr tmp;
        if (nullptr == bi_tree->right)
        {
            tmp = bi_tree;
            bi_tree = bi_tree->left;
            delete tmp;
        }
        else if (nullptr == bi_tree->left)
        {
            /*右為空，刪除父節點，左頂上*/
            tmp = bi_tree;
            bi_tree = bi_tree->right;
            delete tmp;
        }
        else
        {
            /*先往右找大的節點*/
            BiTreeTypePtr p = bi_tree->right;
            tmp = p;
            /*往左找最接近的值，後繼值*/
            while (nullptr != p->left)
            {
                tmp = p;
                p = p->left;
            }
           
            /*後繼節點的值給刪除節點，然後後繼節點的父節點左子樹指向後繼節點的右子樹*/
            bi_tree->node_data = p->node_data;
            tmp->left = p->right;
            delete p;
        }
        
        return true;
    }
}

這時候可能有疑問，說添加節點為什麼不直接搞成遞歸，還準們搞了一個搜索介面在裡面，我的回答是完全可以的。

那麼二叉排序樹的搜索、添加、刪除的代碼綜合如下：

先補上makefile，然後弄上代碼，本人懶了一下，所有的驗證代碼都寫在了構造函數中，沒有寫在main函數中。

如果對makefile不瞭解，在linux下創建一個文件，命名makefile,拷貝下麵的makefile中的內容到創建makefile中，然後將代碼

拷貝到main.cpp中，直接敲命令make就可以進行編譯

註：如果linux中gcc版本過低，就是通過gcc -v查看到的版本發現低於4.7的，可以按如下方式做

　　1）將makefile中-std=c++11刪除

　　2）將nullptr改為NULL

　　3）to_string可以用如下代碼代替

#pragma once

#include <string>
#include <sstream>

using std::string;
using std::stringstream;

template <typename ValType>
string ToString(ValType val)
{
    stringstream ss;
    ss << val;
    return ss.str();
}

makefile和代碼如下：

CC := g++

EXEC = bbst_test

RELEASE = ./

INCLUDES = -I. \

CFLAGS = $(INCLUDES) -Wall -O3 -std=c++11

LIBS = -L$(RELEASE)

CPPPATH = ./main.cpp

$(EXEC):
        $(CC) -o $(EXEC) $(CFLAGS) $(CPPPATH) $(LIBS)

clean:
        rm -rf *.o $(EXEC)
makefile 
#include <string>
#include <iostream>
#include <cstdio>
#include <map>

using std::string;
using std::cout;
using std::endl;
using std::map;
using std::to_string;

typedef struct _BiTree
{
    int node_data;

    int bf;

    int height;

    int position;
    int splice;

    struct _BiTree *left;
    struct _BiTree *right;
    _BiTree(int data)
        : node_data(data), bf(0), height(0),
        position(0), splice(0), left(nullptr), right(nullptr)
    {}
}BiTreeType, *BiTreeTypePtr;

class BBST
{
public:
    BBST()
    {
        int arr[] = {49, 38, 65, 97, 76, 13, 27, 50};
//        int arr[] = {2,1,0,3,4,5,6,9,8,7};

        m_bi_tree_depth = 0;
        m_root_ptr = nullptr;
        for (unsigned i=0; i<sizeof(arr)/sizeof(arr[0]); ++i)
        {
            InsertNode(m_root_ptr, arr[i]);
        }

        PromptExistBiTree();

    }
    
    ~BBST()
    {
        Destory(m_root_ptr);
    }

private:

    void Destory(BiTreeTypePtr &bi_tree)
    {
        if (bi_tree)
        {
            Destory(bi_tree->left);
            Destory(bi_tree->right);

            delete bi_tree;
            bi_tree = nullptr;
        }
    }
    

    bool SearchBBST(BiTreeTypePtr bi_tree, int data, BiTreeTypePtr parent, BiTreeTypePtr &choose_node)
    {
        if (nullptr == bi_tree)
        {
            /*找到了最後為空的位置，沒有找到節點，記錄父節點，方便添加*/
            choose_node = parent;
            return false;
        }        
        else if (bi_tree->node_data == data)
        {
            choose_node = bi_tree;
            return true;
        }
        else if (bi_tree->node_data > data)
        {
            return SearchBBST(bi_tree->left, data, bi_tree, choose_node);
        }
        else
        {
            return SearchBBST(bi_tree->right, data, bi_tree, choose_node);
        }
    }

    bool InsertNode(BiTreeTypePtr &bi_tree, int data)
    {
        /*根節點*/
        if (bi_tree == nullptr)
        {
            BiTreeTypePtr node = new BiTreeType(data);
            bi_tree = node;
            return true;
        }

        /*在已存的二叉樹中查找節點，如果不存在，就找到合適的位置加入節點*/
        BiTreeTypePtr p = nullptr;
        if (!SearchBBST(bi_tree, data, nullptr, p))
        {
            BiTreeTypePtr node = new BiTreeType(data);
            if (p->node_data > data)
            {
                p->left = node;
            }
            else
            {
                p->right = node;
            }
            
            return true;
        }

        return false;
    }

    bool DeleteNode(BiTreeTypePtr &bi_tree, int data)
    {
        if (nullptr == bi_tree)
        {
            return false;
        }
        else if (bi_tree->node_data > data)
        {
            return DeleteNode(bi_tree->left, data);
        }
        else if (bi_tree->node_data < data)
        {
            return DeleteNode(bi_tree->right, data);
        }
        else
        {
            /*左為空，刪除父節點，右頂上*/
            BiTreeTypePtr tmp;
            if (nullptr == bi_tree->right)
            {
                tmp = bi_tree;
                bi_tree = bi_tree->left;
                delete tmp;
            }
            else if (nullptr == bi_tree->left)
            {
                /*右為空，刪除父節點，左頂上*/
                tmp = bi_tree;
                bi_tree = bi_tree->right;
                delete tmp;
            }
            else
            {
                /*先往右找大的節點*/
                BiTreeTypePtr p = bi_tree->right;
                tmp = p;
                /*往左找最接近的值，後繼值*/
                while (nullptr != p->left)
                {
                    tmp = p;
                    p = p->left;
                }

                /*後繼節點的值給刪除節點，然後後繼節點的父節點左子樹指向後繼節點的右子樹*/
                bi_tree->node_data = p->node_data;
                tmp->left = p->right;
                delete p;
            }
            
            return true;
        }
    }

    void PromptExistBiTree()
    {
        m_level_str_map.clear();
        m_bi_tree_depth = 0;
        MarkNodeHeight(m_root_ptr, 0);
        MarkBinaryTree(m_root_ptr, GetRootPosition(m_bi_tree_depth));
        SpliceBiTreeStr(m_root_ptr);

        PaintBiTree();
    }

    void MarkNodeHeight(BiTreeTypePtr &bi_tree, int height)
    {
        if (bi_tree == nullptr)
        {
            return;
        }
        
        bi_tree->height = height;
        if (height > m_bi_tree_depth)
        {
            m_bi_tree_depth = height;
        }

        if (bi_tree->left != nullptr)
        {
            MarkNodeHeight(bi_tree->left, height + 1);
        }

        if (bi_tree->right != nullptr)
        {
            MarkNodeHeight(bi_tree->right, height + 1);
        }
    }

    void MarkBinaryTree(BiTreeTypePtr &bi_tree, int position)
    {
        if (bi_tree == nullptr)
        {
            return;
        }
        
        bi_tree->position = position;
        bi_tree->splice = GetRootSplice(m_bi_tree_depth - bi_tree->height);
    
//        cout << bi_tree->height << ":" << bi_tree->splice << ":" << bi_tree->position << ":" << bi_tree->data << endl;

        if (bi_tree->left != nullptr)
        {
            MarkBinaryTree(bi_tree->left, position - GetRootPosition(m_bi_tree_depth - bi_tree->height - 1) - 1);
        }

        if (bi_tree->right != nullptr)
        {
            MarkBinaryTree(bi_tree->right, position + GetRootPosition(m_bi_tree_depth - bi_tree->height - 1) + 1);
        }
    }

    void SpliceBiTreeStr(BiTreeTypePtr &bi_tree)
    {
        if (bi_tree != nullptr)
        {
            string p_str = FindLevelStr(bi_tree->splice);

            if (!p_str.empty())    
            {                
                p_str.append(bi_tree->position - p_str.size(), ' ');
            }
            else
            {            
                p_str.append(bi_tree->position, ' ');
            }

            p_str.append(to_string(bi_tree->node_data));                
            m_level_str_map[bi_tree->splice] = p_str;
            
#if 1
            if (bi_tree->height != m_bi_tree_depth)
            {
                int brance_splice = GetRootPosition(m_bi_tree_depth - bi_tree->height - 1);
                for (int i=1; i<=brance_splice; ++i)
                {
                    string brance_str = FindLevelStr(bi_tree->splice - i);
                    
                    if (!brance_str.empty())
                    {
                        brance_str.append(bi_tree->position - brance_str.size() - i, ' ');    
                    }
                    else
                    {
                        brance_str.append(bi_tree->position - i, ' ');
                    }

                    if (bi_tree->left != nullptr)
                    {
                        brance_str.append("/");
                    }
                    else
                    {
                        brance_str.append(" ");
                    }


                    if (bi_tree->right != nullptr)
                    {
                        brance_str.append(i*2 - 1, ' ');
                        brance_str.append("\\");
                    }
                                            
                    m_level_str_map[bi_tree->splice - i] = brance_str;
                }
            }
#endif
            if (bi_tree->left != nullptr)
            {
                SpliceBiTreeStr(bi_tree->left);
            }

            if (bi_tree->right != nullptr)
            {
                SpliceBiTreeStr(bi_tree->right);
            }
        }
    }

    void PaintBiTree()
    {
        int splice = -1;
        while ((splice = SelectLowestNode()) != -1)
        {
            cout << m_level_str_map[splice] << endl;
            m_level_str_map.erase(splice);
        }
    }

    int SelectLowestNode()
    {
        int mininal_num = -1;
        for (auto map_pair : m_level_str_map)
        {
            if (map_pair.first > mininal_num)
            {
                mininal_num = map_pair.first;
            }
        }

        return mininal_num;
    }

    int GetRootPosition(int height)
    {
        return abs(GetPrintSide(height, 1) * 3 - 1);
    }

    int GetRootSplice(int height)
    {
        int splice_num = GetPrintSide(height, 1) * 3 - 1;
        return (splice_num > 0) ? splice_num : 0;
    }

    int GetPrintSide(int height, int side)
    {
        if (height <= 0)
        {
            return 0;
        }
        else if (height == 1)
        {
            return side;
        }
        else
        {
            return GetPrintSide(height-1, side*2);
        }
    }

    string FindLevelStr(int splice)
    {
        string tmp_str;
        for (auto node : m_level_str_map)
        {
            if (node.first == splice)
            {
                return node.second;
            }
        }

        return tmp_str;
    }

private:
    BiTreeTypePtr m_root_ptr;

    int m_bi_tree_depth;

    map<int, string> m_level_str_map;
};

int main()
{
    BBST bb_st;
    
    return 0;
}
二叉排序樹search、insert、delete

 代碼中的PromptExistBiTree為列印介面，會以樹形列印數據，可以在你想調試的代碼的位置列印數據，比如可以放在插入介面中

列印邏輯如下圖，可以對著代碼看

 

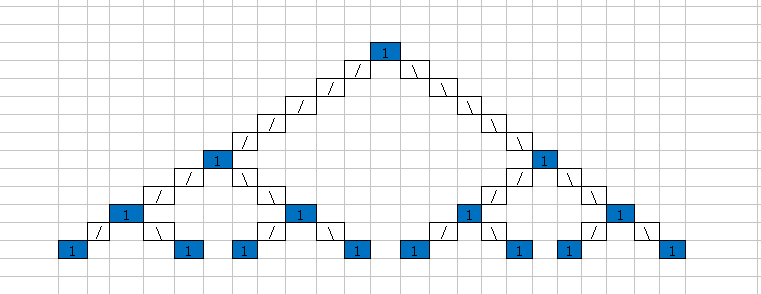
運行完的結果應該如下：

您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • Java併發系列[9]----ConcurrentHashMap源碼分析
    我們知道哈希表是一種非常高效的數據結構，設計優良的哈希函數可以使其上的增刪改查操作達到O(1)級別。Java為我們提供了一個現成的哈希結構，那就是HashMap類，在前面的文章中我曾經介紹過HashMap類，知道它的所有方法都未進行同步，因此在多線程環境中是不安全的。為此，Java為我們提供了另外一 ...
  • 白話python3、c語言和javascript的hello world表述（開篇版）
    有一句段子流傳很久。 我精通各種語言的hello world !。 因為比如python3、c語言和javascript與學習網路安全關係非常大，所以說，對這幾門語言的關註比較多。 但是，在kali上學習的時候有一些東西非常值得註意，否則非常的耽誤時間，因為在這上面白白浪費了幾個小時的代價，所以說， ...
  • 18.C++-[ ]操作符使用 、函數對象與普通函數區別(詳解)
    在上章17.C++-string字元串類(詳解)學習了string類,發現可以通過[ ]重載操作符來訪問每個字元。 比如: 接下來,我們來自己寫個[ ]重載操作符,來模擬string類 運行列印: 函數對象 函數對象是指該對象具備函數的行為 函數對象,是通過()調用操作符聲明得到的,然後便能通過函數 ...
  • thinkphp5 taglib自定義標簽教程
    學著寫了一下，終於搞定了，順便分享一下！taglib是tp框架自定義標簽功能，如果你用過cms，肯定見過類似： 或者： 這樣的操作，這對於開發工作是挺方便的，所以覺得有必要看下tp的taglib，教程如下：1 、在common（我是在common，你自己看，反正是用命名空間載入）里新建目錄tagli ...
  • CDN的作用與基本過程
    簡介 CDN，Content Distribute Network，可以直譯成內容分髮網絡，CDN解決的是如何將數據快速可靠從源站傳遞到用戶的問題。用戶獲取數據時，不需要直接從源站獲取，通過CDN對於數據的分發，用戶可以從一個較優的伺服器獲取數據，從而達到快速訪問，並減少源站負載壓力的目的。 動機 ...
  • python中強大優雅的列表推導表達式
    推導表達式其實就是簡化一些迴圈判斷操作等 生成一個數字1-10的列表，可以有多少種方法？ 現在看下推導表達式 有些人，可能會說，直接range( 1, 11 )就好了，多此一舉，如果我們要篩選出奇數? 當然，range依然能夠做到： 那，如果要得到偶數，需要遍歷每一項，判斷 他等價於如下的推導表達式 ...
  • 每個 Java 開發者都應該知道的 5 個註解
    自 JDK5 推出以來，註解已成為Java生態系統不可缺少的一部分。雖然開發者為Java框架（例如Spring的@Autowired）開發了無數的自定義註解，但編譯器認可的一些註解非常重要。 在本文中，我們將看到5個Java編譯器支持的註解，並瞭解其期望用途。順便，我們將探索其創建背後的基本原理，圍 ...
  • JSP學習（JavaBean）
    Java Web學習 一、搭建java web開發環境： （1）安裝jdk （2）安裝Tomcat伺服器（Apache的開源項目），安裝Tomcat並設置環境變數 （3）安裝EclipseEE（或者MyEclipse） 二、WEB-INF安全目錄介紹（只有伺服器可以訪問） （1）web.xml文件（ ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類