一.冒泡排序 原理:簡單來說就是相鄰兩個元素進行對比,按照你需要的排序方式(升序or降序)進行位置替換,替換時需要額外一個變數當作中間變數去暫存值。 總結步驟: 1、外迴圈是遍歷每個元素,每次都放置好一個元素; 2、內迴圈是比較相鄰的兩個元素,把大/小的元素交換到後面; 3、等到第一步中迴圈好了以後 ...
一.冒泡排序
原理:簡單來說就是相鄰兩個元素進行對比,按照你需要的排序方式(升序or降序)進行位置替換,替換時需要額外一個變數當作中間變數去暫存值。
總結步驟:
1、外迴圈是遍歷每個元素,每次都放置好一個元素;
2、內迴圈是比較相鄰的兩個元素,把大/小的元素交換到後面;
3、等到第一步中迴圈好了以後也就說明全部元素排序好
function Bubble(arr) { for (let i = 0; i < arr.length; i++) {//遍曆數組每一個(回合數) for (let j = 0; j < arr.length - 1 - i; j++) {//真正進行比較,例:i=0時比較第一次,進入第二層迴圈arr[0]與arr[1]進行比較,符合交換條件即交換,不符合繼續比較 if (arr[j] < arr[j + 1]) { let temp = arr[j + 1]//交換變數 arr[j + 1] = arr[j] arr[j] = temp } } } return arr }
時間複雜度:http://blog.csdn.net/itachi85/article/details/54882603
最好的情況:數組已經排好序(不用交換元素)-----> 時間花銷為:[ n(n-1) ] / 2;所以最優的情況時間複雜度為:O( n^2 )
最差的情況:也就是開始的時候元素是逆序的,那麼每一次排序都要交換兩個元素,則時間花銷為:[ 3n(n-1) ] / 2;(其中比上面最優的情況所花的時間就是在於交換元素的三個步驟);所以最差的情況下時間複雜度為:O( n^2 );
綜上:
最優的時間複雜度為:O( n^2 ) ;//當使用標誌位方法來判斷你是否排好序時,時間複雜度為O(n)
最差的時間複雜度為:O( n^2 );
平均的時間複雜度為:O( n^2 );
加上flag的代碼如下:
function bubbleSort2(arr) {var i = arr.length-1; //初始時,最後位置保持不變 while ( i> 0) { var flag= 0; //每趟開始時,無記錄交換 for (var j= 0; j< i; j++) if (arr[j]> arr[j+1]) { flag= j; //記錄交換的位置,flag之後的均已交換成功 var tmp = arr[j];
arr[j]=arr[j+1];
arr[j+1]=tmp; } i= flag; //為下一趟排序作准備,只要掃描到flag位置即可 }return arr; }
二:選擇排序
原理:首先從原始數組中找到最小的元素,並把該元素放在數組的最前面,然後再從剩下的元素中尋找最小的元素,放在之前最小元素的後面,直到排序完畢
function Choose(arr) { let maxIndex, temp; for (let i = 0; i < arr.length - 1; i++) { maxIndex = i//maxIndex始終作為最大值的位置索引, for (let j = i + 1; j < arr.length; j++) {//當前最大值的後一位開始比較 if (arr[j] > arr[maxIndex]) {//當後一位大於當前maxIndex maxIndex = j//將最大位置的索引值變為兩者中較大的 } } temp = arr[i]//當前輪次中的i與最大值進行交換,以達成最大值在前的的目的 arr[i] = arr[maxIndex] arr[maxIndex] = temp } return arr }
時間複雜度:
平均時間複雜度:O(n*n)
最好情況:O(n*n)
最差情況:O(n*n)
三:插入排序
原理:一組數據分成兩組,分別將其稱為有序組與待插入組。每次從待插入組中取出一個元素,與有序組的元素進行比較,並找到合適的位置,將該元素插到有序組當中。就這樣,每次插入一個元素,有序組增加,待插入組減少。直到待插入組元素個數為0。
function InsertionSort(array) { var length = array.length; for (var i = 0; i < length - 1; i++) {//i代表已經排序好的序列最後一項下標(第一項已排好序) var insert = array[i + 1];//insert為待插入組的第一項 var index = i + 1;//記錄要被插入的下標 for (var j = i; j >= 0; j--) { if (insert > array[j]) //要插入的項比它小/大,往後移動 array[j + 1] = array[j]; index = j; } } array[index] = insert; } return array; }
時間複雜度:
平均時間複雜度:O(n*n)
最好情況:O(n)
最差情況:O(n*n)
四:希爾排序(屬於插入排序的一種)
原理:利用步長來進行兩兩元素比較,然後縮減步長在進行排序。
複製了一個詳細的說明:希爾排序的實質是分組插入排序,該方法又稱縮小增量排序。該方法的基本思想是:先將整個待排元素序列分割為若幹個子序列(由相隔某個‘增量’的元素組成的)分別進行直接插入排序,然後依次縮減增量再進行排序,帶這個序列中的元素基本有序(增量足夠小)時,再對全體元素進行一次直接插入排序。因為直接插入排序在元素基本有序的情況下(接近最好情況)效率是很高的,因此希爾排序在時間效率上有較大的提高。
希爾排序演算法實現。
與插入排序的不同之處:它會優先比較距離較遠的元素
function shellSort(arr) { let temp, gap = 1; while (gap < arr.length / 3) { gap = gap * 3 + 1//動態定義間隔序列 } for (gap; gap > 0; gap = Math.floor(gap / 3)) {//控制步長(間隔)並不斷縮小 for (var i = gap; i < arr.length; i++) {//按照增量個數對序列進行排序 temp = arr[i] for (var j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {//例:j=0 arr[1]>arr[5] arr[j + gap] = arr[j] } arr[j + gap] = temp } } return arr }
時間複雜度:
最佳情況: O(nlog2 n)
最壞情況: O(nlog2 n)
平均情況: O(nlog n)
五:歸併排序
原理:採用分治法,先劃分,再合併
步驟:
1.先將C劃分為兩個數組A和B(即把數組C從中間分開)
2.再分別對數組A、B重覆步驟1的操作,逐步劃分,直到不能再劃分為止(每個子數組只剩下一個元素),這樣,劃分的過程就結束了。
如: [12 20 30 21 15 33 26 19 40 25]
劃分為: [12 20 30 21 15] [33 26 19 40 25]
[12 20] [30 21 15] [33 26] [19 40 25]
[12] [20] [30] [21 15] [33] [26] [19] [40 25]
[12] [20] [30] [21] [15] [33] [26] [19] [40] [25]
3.然後從下層往上層不斷合併數組,每一層合併相鄰的兩個子數組,合併的過程是每次從待合併的兩個子數組中選取一個最小的元素,然後把這個元素放到合併後的數組中,不斷重覆直到把兩個子數組的元素都放到合併後的數組為止。
4.依次類推,直到合併到最上層結束,這時數據的排序已經完成了。
function mergeSort(arr) { if (arr.length < 2) { return arr; } //將數組分為左右兩個子序列 let middle = Math.floor(arr.length / 2) let left = arr.slice(0, middle) let right = arr.slice(middle) return merge(mergeSort(left), mergeSort(right))//對兩個子序列重覆劃分為兩個進行排序,直到不能劃分 } function merge(left, right) { let result = [] while (left.length > 0 && right.length > 0) { if (left[0] < right[0]) {//兩兩比較,較小的放入結果數組 result.push(left.shift())//shift()方法刪除數組第一個元素,並返回被刪除的元素 } else { result.push(right.shift()) } } /* 當左右數組長度不等.將比較完後剩下的數組項鏈接起來即可 */ return result.concat(left).concat(right); }
時間複雜度:
最佳情況:T(n) = O(n)
最差情況:T(n) = O(nlogn)
平均情況:T(n) = O(nlogn)
六:快速排序
原理:選擇一個基準,將比基準小的放左邊,比基準小的放在右邊(基準處在中間位置)
function quickSort2(arr) { //如果數組<=1,則直接返回 if (arr.length <= 1) { return arr; } var pivotIndex = Math.floor(arr.length / 2); //找基準,並把基準從原數組刪除 var pivot = arr.splice(pivotIndex, 1) [0]; //定義左右數組 var left = []; var right = []; //比基準小的放在left,比基準大的放在right for (var i = 0; i < arr.length; i++) { if (arr[i] <= pivot) { left.push(arr[i]); } else { right.push(arr[i]); } } //遞歸 return quickSort2(left).concat([pivot], quickSort2(right)); }
時間複雜度:
最佳情況:T(n) = O(nlogn)
最差情況:T(n) = O(n2)
平均情況:T(n) = O(nlogn)
排序演算法所有時間複雜度及空間複雜度,穩定性等:
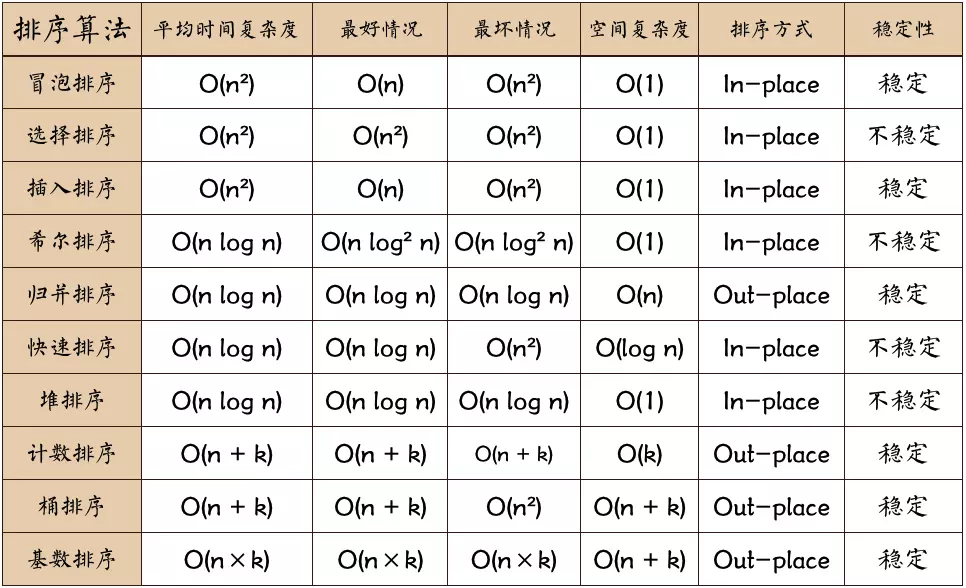
掘金的這個文章寫的很詳細:https://juejin.im/post/57dcd394a22b9d00610c5ec8



