博弈論進階之樹的刪邊游戲與無向圖的刪邊游戲

PS:本文內容大部分借(chao)鑒(xo)自yhqz

樹的刪邊游戲

給出一個有 N個點的樹，有一個點作為樹的根節點。游戲者輪流從樹中刪去邊，刪去一條邊後，不與根節點相連的部分將被移走。誰無法移動誰輸。

結論

葉子節點的SG值為0；中間節點的SG值為它的所有子節點的SG值加1後的異或和。

證明

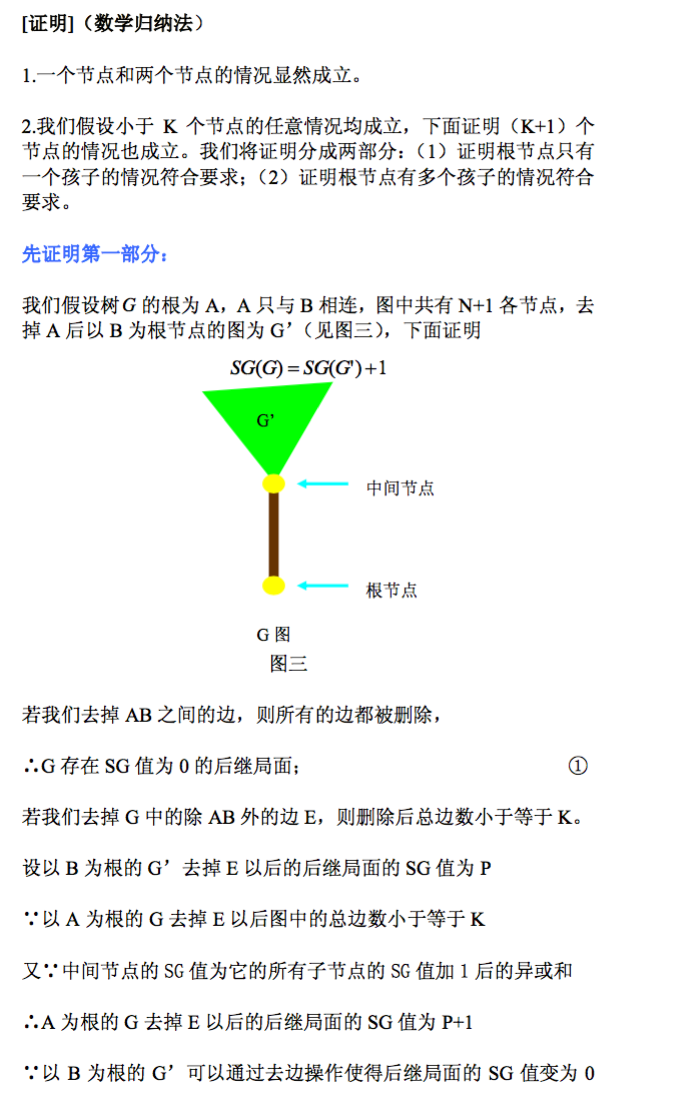
無向圖的刪邊游戲

一個無相聯通圖，有一個點作為圖的根。

游戲者輪流從圖中刪去邊，刪去一條邊後，不與根節點相連的部分將被移走。

誰無路可走誰輸。

結論

對於這個模型，有一個著名的定理——Fusion Principle

我們可以對無向圖做如下改動：將圖中的任意一個偶環縮成一個新點，任意一個奇環縮成一個新點加一個新邊；所有連到原先環上的邊全部改為與新點相連。這樣的改動不會影響圖的SG 值。

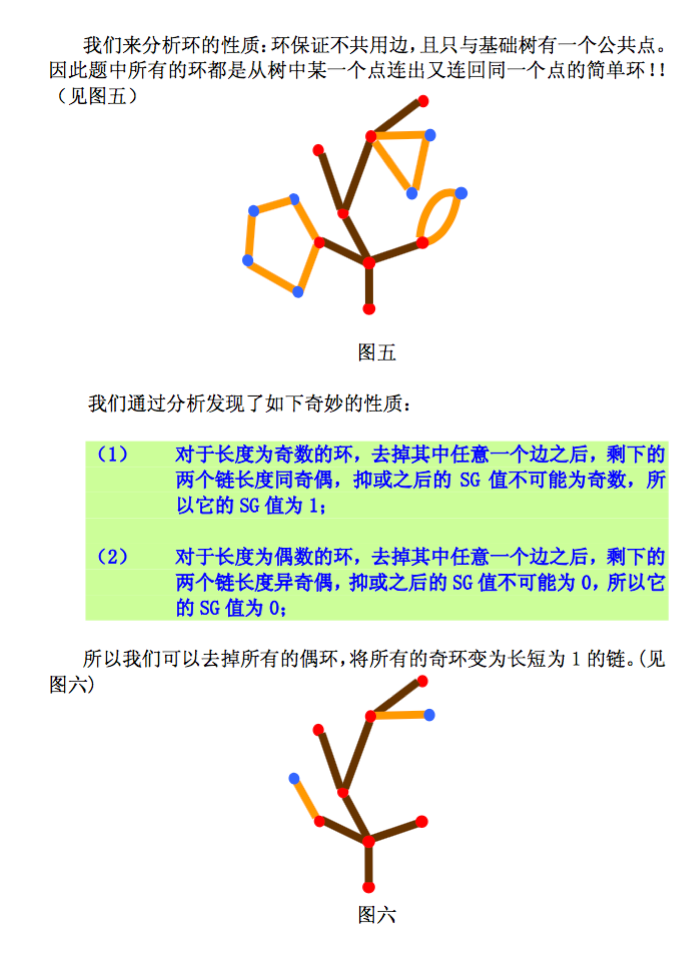
這樣的話，我們可以將任意一個無向圖改成樹結構，“無向圖的刪邊游戲”就變成了“樹的刪邊游戲”。