動態規劃問題----國王和金礦_ZenDei技術網路在線

動態規劃問題----國王和金礦

-Advertisement-

問題：有一個國家發現了5座金礦，每座金礦的黃金儲量不同，需要參與挖掘的工人數也不同。參與挖礦工人的總數是10人。每座金礦要麼全挖，要麼不挖，不能派出一半人挖取一半金礦。要求用程式求解出，要想得到儘可能多的黃金，應該選擇挖取哪幾座金礦？動態規劃有三個核心元素：最優子結構、邊界、狀態轉移方程式。 ...

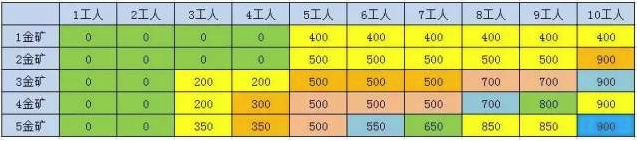
問題：有一個國家發現了5座金礦，每座金礦的黃金儲量不同，需要參與挖掘的工人數也不同。參與挖礦工人的總數是10人。每座金礦要麼全挖，要麼不挖，不能派出一半人挖取一半金礦。要求用程式求解出，要想得到儘可能多的黃金，應該選擇挖取哪幾座金礦？

動態規劃有三個核心元素：最優子結構、邊界、狀態轉移方程式。該問題中要求10個工人5個金礦，挖最多黃金的選擇。因此最優子結構有兩種情況：

10個工人4個金礦時，挖出最多黃金的選擇。
4金礦，工人數：10-最後一個金礦需要的人數。

我們把金礦數量設為n，工人數設為m，金礦的黃金量設為g[]，金礦的用工量設為數組p[],該問題中，各數據如下所示： n=5, m=10, g = [400,500,200,300,350], p = [5,5,3,4,3] 那麼5座金礦和4做金礦的最優選擇之間存在這樣的關係：F(5,10) = MAX(F(4,10),F(4,10-P[4]+G[4])) 現在給出邊界，也就是金礦數量n為1時：當n=1，m>=p[0]時，F(n,m) = g[0]; 當n=1，m<p[0]時，F(n,m) = 0; 使用格子推導出所有的情況：

對某一情況進行分析，如F(3,8)，其結果就是MAX(F(2,8),F(2,8-P[3]) + G[3]) = 700 狀態轉移方程： F(n,m) = 0 (n<=1,m<p[0]); F(n,m) = g[0](n==1,m>=p[0]); F(n,m) = F(n-1,m)(n>1,m<p[n-1]); F(n,m) = max(F(n-1,m), F(n-1,m-p[n-1])+g[n-1])(n>1,m>=p[n-1]); js代碼如下： //n:金礦數量 m:工人數量 g:獲得金額數組 p:需要工人數組 function getMostGold(n,m,g,p){ var preResults = []; var results = []; for(var i = 0; i <= m; i++){ if(i < p[0]){ preResults[i] = 0; }else{ preResults[i] = g[0]; } } for(var t = 0;t < preResults.length; t++){ results[t] = preResults[t]; } if(n == 1){ return results[m]; } for(var i = 1;i < n; i++){ for(var j = 0; j <= m; j++){ if(j < p[i]){ results[j] = preResults[j]; }else{ //實際上就是管不管最後一個金礦的問題 results[j] = Math.max(preResults[j],preResults[j-p[i]] + g[i]); } } console.log(results); for(var t = 0;t < preResults.length; t++){ preResults[t] = results[t]; } } return results[m]; } var g = [400,500,200,300,350]; var p = [5,5,3,4,3]; console.log(getMostGold(5,10,g,p)); 其中需要註意的是，js中數組拷貝需要使用深拷貝，使用淺拷貝（preResults = results）會產生數據問題。原文鏈接如下：http://www.sohu.com/a/153858619_466939

您的分享是我們最大的動力!

-Advertisement-

更多相關文章

Linux開機自動掛載文件fstab介紹

這個文件描述系統中各種文件系統的信息。一般而言，應用程式僅讀取這個文件，而不對它進行寫操作。對它的維護是系統管理員的工作。 ...
mysql數據表的基本操作:表結構操作，欄位操作

本節介紹：表結構操作創建數據表、查看數據表和查看欄位、修改數據表結構刪除數據表欄位操作新增欄位、修改欄位數據類型、位置或屬性、重命名欄位刪除欄位首發時間：2018-02-18 21:31 表結構操作創建數據表：語法： create table [if not exists... ...
Android安卓Die With Me不限電量破解版出爐,初二學生就能做到,你為什麼不能?

Android安卓Die With Me不限電量破解版出爐,初二學生就能做到,你為什麼不能? ...
新體能評定軟體開發總結（一）

轉載請註明來源。加入新特性：對話框，NumberPicker，專項訓練入口界面，新兵、文職人員專欄，自動更新。總結問題： 1. startActivityForResult(Intent intent,int requestCode)中requestCode要是自然數，否則返回後不會調用onA ...
獲取View組件寬度以及ViewTreeObserver

View寬高測量方法：測量方法有三種，如下： 1）（直接在onCreate()執行） 2）2和3都是在onCreate()調用完後回調拿到組件的寬高 3）註意：方法一比其他方法多一次onMeasure計算，方法二的回調函數會被多次調用。轉自http://blog.csdn.net/johnny ...
js部分方法整理

JavaScript數組的方法不完全整理（未完待續：JavaScript字元串的方法不完全整理2018年2月18日20:52:42） ...
網頁設計學習筆記（1）

3 添加標題圖片首先，要加入圖標，需要.ico格式的圖片才可以。可以在：http://www.bitbug.net/ 這裡上傳圖片，製成.ico格式的文件。然後在html的<head>標簽中插入： <link rel="shortcut icon" href="WEB-INF/favicon. ...
關於部署網站的筆記

近期幫助別人做了個網站需要能在網路上訪問。本人也是第一次製作網站，不斷摸索之後終於成功了。下麵是過程及遇到的問題解決筆記。一、購買功能變數名稱和伺服器我的功能變數名稱和伺服器都是在騰訊雲上購買的。流程騰訊雲上都有，就是功能變數名稱的備案時間比較長。伺服器購買好之後需要安裝好操作系統。我安裝的是windows serv ...