基於 Keras 用 LSTM 網路做時間序列預測

来源:https://www.cnblogs.com/xuruilong100/archive/2018/02/17/8451790.html
-Advertisement-
Play Games

基於 Keras 用 LSTM 網路做時間序列預測 本文主要參考了 Jason Brownlee 的博文 "Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras" 原文使用 python 實現模 ...


基於 Keras 用 LSTM 網路做時間序列預測

本文主要參考了 Jason Brownlee 的博文 Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras

原文使用 python 實現模型，這裡是用 R

時間序列預測是一類比較困難的預測問題。

與常見的回歸預測模型不同，輸入變數之間的“序列依賴性”為時間序列問題增加了複雜度。

一種能夠專門用來處理序列依賴性的神經網路被稱為 遞歸神經網路（Recurrent Neural Networks、RNN）。因其訓練時的出色性能，長短記憶網路（Long Short-Term Memory Network，LSTM）是深度學習中廣泛使用的一種遞歸神經網路（RNN）。

在本篇文章中，將介紹如何在 R 中使用 keras 深度學習包構建 LSTM 神經網路模型實現時間序列預測。

文章的主要內容：

  • 如何為基於回歸、視窗法和時間步的時間序列預測問題建立對應的 LSTM 網路。
  • 對於非常長的序列，如何在構建 LSTM 網路和用 LSTM 網路做預測時保持網路關於序列的狀態（記憶）。

問題描述

“航班旅客數據”是一個常用的時間序列數據集，該數據包含了 1949 至 1960 年 12 年間的月度旅客數據，共有 144 個觀測值。

下載鏈接：international-airline-passengers.csv

長短記憶網路

長短記憶網路，或 LSTM 網路，是一種遞歸神經網路（RNN），通過訓練時在“時間上的反向傳播”來剋服梯度消失問題。

LSTM 網路可以用來構建大規模的遞歸神經網路來處理機器學習中複雜的序列問題，並取得不錯的結果。

除了神經元之外，LSTM 網路在神經網路層級（layers）之間還存在記憶模塊。

一個記憶模塊具有特殊的構成，使它比傳統的神經元更“聰明”，並且可以對序列中的前後部分產生記憶。模塊具有不同的“門”（gates）來控制模塊的狀態和輸出。一旦接收並處理一個輸入序列，模塊中的各個門便使用 S 型的激活單元來控制自身是否被激活，從而改變模塊狀態並向模塊添加信息（記憶）。

一個激活單元有三種門：

  • 遺忘門（Forget Gate）：決定拋棄哪些信息。
  • 輸入門（Input Gate）：決定輸入中的哪些值用來更新記憶狀態。
  • 輸出門（Output Gate）：根據輸入和記憶狀態決定輸出的值。

每一個激活單元就像是一個迷你狀態機，單元中各個門的權重通過訓練獲得。

LSTM 網路回歸

時間序列預測中最簡單的思路之一便是尋找當前和過去數據（\(X_t, X_{t-1}, \dots\)）與未來數據（$ X_{t+1}$）之間的關係，這種關係通常會表示成為一個回歸問題。

下麵著手將時間序列預測問題表示成一個回歸問題，並建立 LSTM 網路用於預測，用 t-1 月的數據預測 t 月的數據。

首先，載入相關 R 包。

library(keras)
library(dplyr)
library(ggplot2)
library(ggthemes)
library(lubridate)

神經網路模型在訓練時存在一定的隨機性，所以要為計算統一隨機數環境。

set.seed(7)

畫出整體數據的曲線圖，對問題有一個直觀的認識。

dataframe <- read.csv(
    'international-airline-passengers.csv')

dataframe$Month <- paste0(dataframe$Month,'-01') %>%
    ymd()

ggplot(
    data = dataframe,
    mapping = aes(
        x = Month,
        y = passengers)) +
    geom_line() +
    geom_point() +
    theme_economist() +
    scale_color_economist()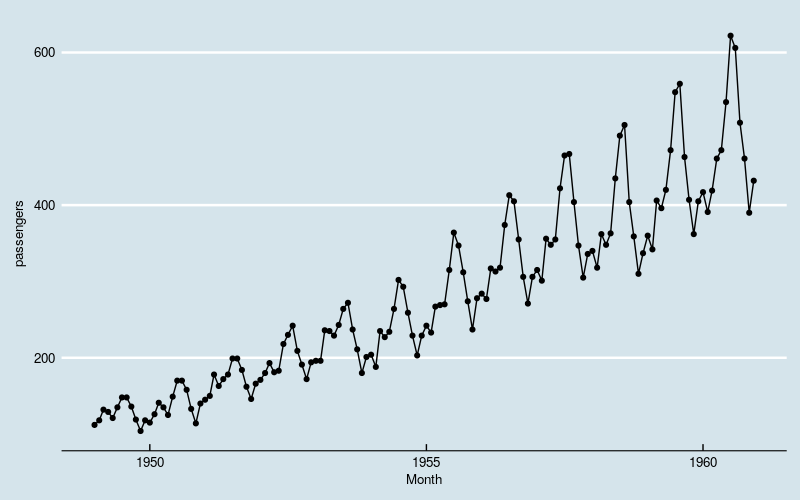

圖1

圖1

數據體現出“季節性”，同時存線上性增長和波動水平增大的趨勢。

將數據集分成兩部分：訓練集和測試集，比例分別占數據集的 2/3 和 1/3。LSTM 網路對數據的“標度”比較敏感，最好將數據縮放到 0 到 1 之間。

max_value <- max(dataframe$passengers)
min_value <- min(dataframe$passengers)
spread <- max_value - min_value

dataset <- (dataframe$passengers - min_value) / spread

create_dataset <- function(dataset,
                           look_back = 1)
{
    l <- length(dataset)
    dataX <- array(dim = c(l - look_back, look_back))

    for (i in 1:ncol(dataX))
    {
        dataX[, i] <- dataset[i:(l - look_back + i - 1)]
    }

    dataY <- array(
        data = dataset[(look_back + 1):l],
        dim = c(l - look_back, 1))

    return(
        list(
            dataX = dataX,
            dataY = dataY))
}

train_size <- as.integer(length(dataset) * 0.67)
test_size <- length(dataset) - train_size

train <- dataset[1:train_size]
test <- dataset[(train_size + 1):length(dataset)]

cat(length(train), length(test))
96 48

為訓練神經網路對數據做預處理，用數據構造出兩個矩陣，分別是“歷史數據”（作為預測因數）和“未來數據”（作為預測目標）。這裡用最近一個月的歷史數據做預測。和一般的回歸問題相比，LSTM 要求輸入數據提供一個額外的維度——時間步。

look_back <- 1
trainXY <- create_dataset(train, look_back)
testXY <-  create_dataset(test, look_back)

dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)

# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], 1, dim_train[2])
dim(testXY$dataX) <- c(dim_test[1], 1, dim_test[2])

下麵構造神經網路的框架結構並用處理過的訓練數據訓練。

model <- keras_model_sequential()

model %>%
    layer_lstm(
        units = 4,
        input_shape = c(1, look_back)) %>%
    layer_dense(
        units = 1) %>%
    compile(
        loss = 'mean_squared_error',
        optimizer = 'adam') %>%
    fit(trainXY$dataX,
        trainXY$dataY,
        epochs = 100,
        batch_size = 1,
        verbose = 2)

訓練結果如下。

trainScore <- model %>%
    evaluate(
        trainXY$dataX,
        trainXY$dataY,
        verbose = 2)

testScore <- model %>%
    evaluate(
        testXY$dataX,
        testXY$dataY,
        verbose = 2)

sprintf(
    'Train Score: %.4f MSE (%.4f RMSE)',
    trainScore * spread^2,
    sqrt(trainScore) * spread)

sprintf(
    'Test Score: %.4f MSE (%.4f RMSE)',
    testScore * spread^2,
    sqrt(testScore) * spread)
[1] "Train Score: 542.2175 MSE (23.2856 RMSE)"
[1] "Test Score: 2420.2046 MSE (49.1956 RMSE)"

把訓練數據的擬合值、測試數據的預測值和原始數據畫在一起。

trainPredict <- model %>%
    predict(
        trainXY$dataX,
        verbose = 2)
testPredict <- model %>%
    predict(
        testXY$dataX,
        verbose = 2)

trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value

df <- data.frame(
    index = 1:length(dataset),
    value = dataset * spread + min_value,
    type = 'raw') %>%
    rbind(
        data.frame(
            index = 1:length(trainPredict) + look_back,
            value = trainPredict,
            type = 'train')) %>%
    rbind(
        data.frame(
            index = 1:length(testPredict) + look_back + length(train),
            value = testPredict,
            type = 'test'))

ggplot(data = df) +
    geom_line(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_point(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_vline(
        xintercept = length(train) + 0.5) +
    theme_economist() +
    scale_color_economist()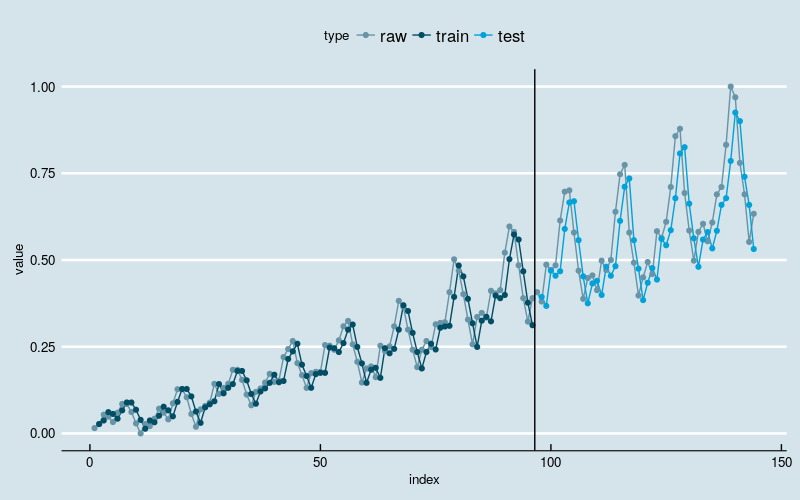

圖2

圖2

黑線左邊是訓練部分，右邊是測試部分。

結果和多層感知機回歸一樣。神經網路模型抓住了數據線性增長和波動率逐漸增加的兩大趨勢，在不做數據轉換的前提下，這是經典的時間序列分析模型不容易做到的；但是很可能沒有識別出“季節性”的結構特點，因為訓練和預測結果和原始數據之間存在“平移錯位”。

LSTM 網路回歸結合視窗法

前面的例子可以看出，如果僅使用\(X_{t-1}\)來預測\(X_t\)，很難讓神經網路模型識別出“季節性”的結構特征，因此有必要嘗試增加“視窗”寬度，使用更多的歷史數據（包含一個完整的周期）訓練模型。

下麵將數 create_dataset 中的參數 look_back 設置為 12，用來包含過去 1 年的歷史數據，重新訓練模型。

set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <-  create_dataset(test, look_back)

dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)

# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], 1, dim_train[2])
dim(testXY$dataX) <- c(dim_test[1], 1, dim_test[2])

model <- keras_model_sequential()

model %>%
    layer_lstm(
        units = 4,
        input_shape = c(1, look_back)) %>%
    layer_dense(
        units = 1) %>%
    compile(
        loss = 'mean_squared_error',
        optimizer = 'adam') %>%
    fit(trainXY$dataX,
        trainXY$dataY,
        epochs = 100,
        batch_size = 1,
        verbose = 2)

trainScore <- model %>%
    evaluate(
        trainXY$dataX,
        trainXY$dataY,
        verbose = 2)

testScore <- model %>%
    evaluate(
        testXY$dataX,
        testXY$dataY,
        verbose = 2)

sprintf(
    'Train Score: %.4f MSE (%.4f RMSE)',
    trainScore * spread^2,
    sqrt(trainScore) * spread)

sprintf(
    'Test Score: %.4f MSE (%.4f RMSE)',
    testScore * spread^2,
    sqrt(testScore) * spread)

trainPredict <- model %>%
    predict(
        trainXY$dataX,
        verbose = 2)
testPredict <- model %>%
    predict(
        testXY$dataX,
        verbose = 2)

trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value

df <- data.frame(
    index = 1:length(dataset),
    value = dataset * spread + min_value,
    type = 'raw') %>%
    rbind(
        data.frame(
            index = 1:length(trainPredict) + look_back,
            value = trainPredict,
            type = 'train')) %>%
    rbind(
        data.frame(
            index = 1:length(testPredict) + look_back + length(train),
            value = testPredict,
            type = 'test'))

ggplot(data = df) +
    geom_line(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_point(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_vline(
        xintercept = length(train) + 0.5) +
    theme_economist() +
    scale_color_economist()
[1] "Train Score: 182.7605 MSE (13.5189 RMSE)"
[1] "Test Score: 1518.8280 MSE (38.9721 RMSE)"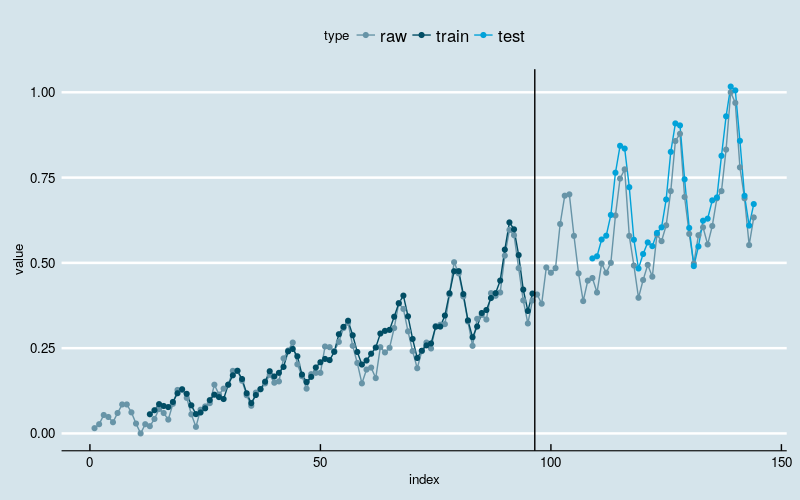

圖3

圖3

結果和多層感知機回歸一樣。新的模型基本上剋服了“平移錯位”的現象，同時依然能夠識別出線性增長和波動率逐漸增加的兩大趨勢。

基於時間步的 LSTM 網路回歸

和一般的回歸問題不同，LSTM 網路的數據輸入包括而外的維度——時間步（time steps）。

一些序列問題的樣本可能有不同數量的時間步。例如，測量現實中一臺機器的故障點或喘振點。每個事件將是一個樣本，觸發事件的觀測正是時間步，而觀察到的變數就是特征。

時間步提供了另一種方式來解釋我們的時間序列問題，就像在視窗法例子那樣，可以將時間序列中之前的時間步作為輸入來預測下一個時間步的輸出。

set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <-  create_dataset(test, look_back)

dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)

# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)

model <- keras_model_sequential()

model %>%
    layer_lstm(
        units = 4,
        input_shape = c(look_back, 1)) %>%
    layer_dense(
        units = 1) %>%
    compile(
        loss = 'mean_squared_error',
        optimizer = 'adam') %>%
    fit(
        trainXY$dataX,
        trainXY$dataY,
        epochs = 100,
        batch_size = 1,
        verbose = 2)

trainScore <- model %>%
    evaluate(
        trainXY$dataX,
        trainXY$dataY,
        verbose = 2)

testScore <- model %>%
    evaluate(
        testXY$dataX,
        testXY$dataY,
        verbose = 2)

sprintf(
    'Train Score: %.4f MSE (%.4f RMSE)',
    trainScore * spread^2,
    sqrt(trainScore) * spread)

sprintf(
    'Test Score: %.4f MSE (%.4f RMSE)',
    testScore * spread^2,
    sqrt(testScore) * spread)

trainPredict <- model %>%
    predict(
        trainXY$dataX,
        verbose = 2)
testPredict <- model %>%
    predict(
        testXY$dataX,
        verbose = 2)

trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value

df <- data.frame(
    index = 1:length(dataset),
    value = dataset * spread + min_value,
    type = 'raw') %>%
    rbind(
        data.frame(
            index = 1:length(trainPredict) + look_back,
            value = trainPredict,
            type = 'train')) %>%
    rbind(
        data.frame(
            index = 1:length(testPredict) + look_back + length(train),
            value = testPredict,
            type = 'test'))

ggplot(data = df) +
    geom_line(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_point(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_vline(
        xintercept = length(train) + 0.5) +
    theme_economist() +
    scale_color_economist()
[1] "Train Score: 370.2546 MSE (19.2420 RMSE)"
[1] "Test Score: 6277.8128 MSE (79.2326 RMSE)"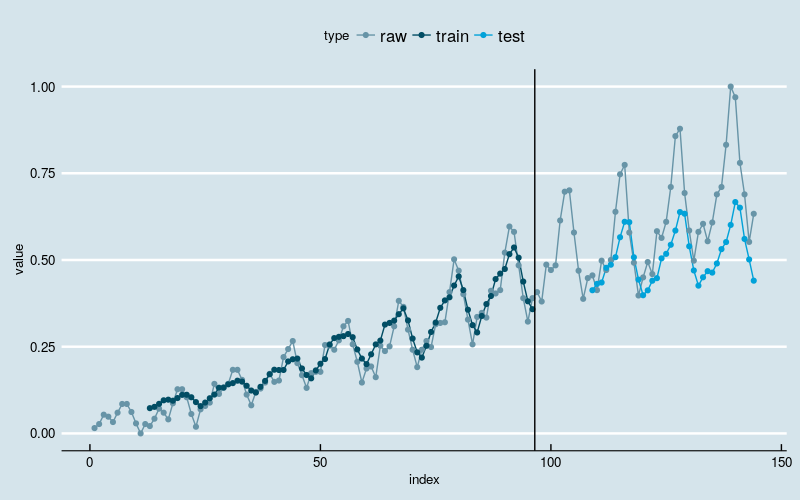

圖4

圖4

很不幸，結果變差了。訓練部分的擬合結果看起來像某種平滑，特別是在最開始的部分。訓練數據的前半部分波動較小，後半部分波動大，擬合的結果反映出神經網路發現了這一點，擬合曲線的波動迅速放大。測試部分的預測結果通常是在低估實際值，說明網路並未“記住”波動放大的趨勢。

在批量訓練之間保持 LSTM 的記憶

LSTM 網路擁有記憶，可以記住長序列中的某些規律或特征。

通常，網路的狀態在訓練過程中會被重置，在調用model.predict() 或 model.evaluate() 時也會。

在 keras 中只要聲明 LSTM 網路是“有狀態的”就可以輕易控制 LSTM 網路中的內部狀態。這意味著可以在訓練和預測過程中保持狀態的穩定。

保持狀態穩定要求訓練數據不能被打亂，同時要在訓練一次之後手動的重置網路狀態。也就是說，每一次迴圈都要訓練一次並重置一次網路狀態。

for (i in 1:100)
{
    model %>%
        fit(trainXY$dataX,
            trainXY$dataY,
            epochs = 1,
            batch_size = batch_size,
            verbose = 2,
            shuffle = FALSE)

    model %>%
        reset_states()
}

最後，LSTM 網路的參數 stateful 必須設置為 TRUE，不同於設定輸入的維度，必須對樣本個數、時間步個數和時間步的特征個數硬編碼。

model %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size, # batch_size
            look_back,  # time_steps
            1),         # features
        stateful = TRUE)

預測也就變成了

model %>%
    predict(
        trainXY$dataX,
        batch_size = batch_size)

完整代碼

set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <-  create_dataset(test, look_back)

dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)

dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)

batch_size = 1

model <- keras_model_sequential()

model %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size,
            look_back,
            1),
        stateful = TRUE) %>%
    layer_dense(
        units = 1) %>%
    compile(
        loss = 'mean_squared_error',
        optimizer = 'adam')

for (i in 1:100)
{
    model %>%
        fit(
            trainXY$dataX,
            trainXY$dataY,
            epochs = 1,
            batch_size = batch_size,
            verbose = 2,
            shuffle = FALSE)

    model %>%
        reset_states()
}

trainPredict <- model %>%
    predict(
        trainXY$dataX,
        batch_size = batch_size,
        verbose = 2)

model %>%
    reset_states()

testPredict <- model %>%
    predict(
        testXY$dataX,
        batch_size = batch_size,
        verbose = 2)

trainScore <- var(trainXY$dataY - trainPredict) * spread^2
testScore <- var(testXY$dataY - testPredict) * spread^2

sprintf(
    'Train Score: %.4f MSE (%.4f RMSE)',
    trainScore,
    sqrt(trainScore))

sprintf(
    'Test Score: %.4f MSE (%.4f RMSE)',
    testScore,
    sqrt(testScore))

trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value

df <- data.frame(
    index = 1:length(dataset),
    value = dataset * spread + min_value,
    type = 'raw') %>%
    rbind(
        data.frame(
            index = 1:length(trainPredict) + look_back,
            value = trainPredict,
            type = 'train')) %>%
    rbind(
        data.frame(
            index = 1:length(testPredict) + look_back + length(train),
            value = testPredict,
            type = 'test'))

ggplot(data = df) +
    geom_line(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_point(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_vline(
        xintercept = length(train) + 0.5) +
    theme_economist() +
    scale_color_economist()
[1] "Train Score: 338.1505 MSE (18.3889 RMSE)"
[1] "Test Score: 2299.0873 MSE (47.9488 RMSE)"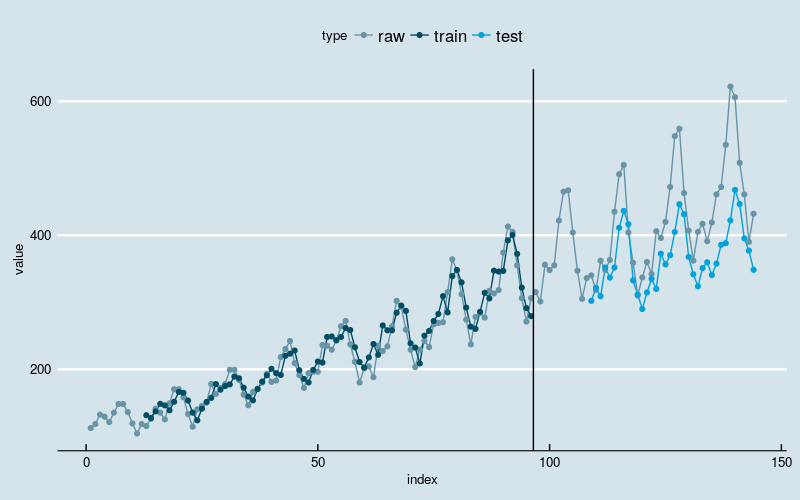

圖5

圖5

和上面的例子相比，沒有明顯改善。

在批量訓練中堆疊 LSTM 網路

最後，介紹一下 LSTM 網路的一大優點：可以通過堆疊構建更深度的神經網路架構。

keras 中 LSTM 網路可以方便的實現堆疊。需要註意的是中間層級的 LSTM 網路的輸出形式必須是序列，只要將參數 return_sequences 設置為 TRUE 就可以了。

擴展前面用到的 LSTM 網路，堆疊兩個層級。

model %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size,
            look_back,
            1),
        stateful = TRUE,
        return_sequences = TRUE) %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size,
            look_back,
            1),
        stateful = TRUE)

完整的代碼

set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <-  create_dataset(test, look_back)

dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)

dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)

batch_size = 1

model <- keras_model_sequential()

model %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size,
            look_back,
            1),
        stateful = TRUE,
        return_sequences = TRUE) %>%
    layer_lstm(
        units = 4,
        batch_input_shape = c(
            batch_size,
            look_back,
            1),
        stateful = TRUE) %>%
    layer_dense(
        units = 1) %>%
    compile(
        loss = 'mean_squared_error',
        optimizer = 'adam')

for (i in 1:100)
{
    model %>%
        fit(trainXY$dataX,
            trainXY$dataY,
            epochs = 1,
            batch_size = batch_size,
            verbose = 2,
            shuffle = FALSE)

    model %>%
        reset_states()
}

trainPredict <- model %>%
    predict(
        trainXY$dataX,
        batch_size = batch_size,
        verbose = 2)

model %>%
    reset_states()

testPredict <- model %>%
    predict(
        testXY$dataX,
        batch_size = batch_size,
        verbose = 2)

trainScore <- var(trainXY$dataY - trainPredict) * spread^2
testScore <- var(testXY$dataY - testPredict) * spread^2

sprintf(
    'Train Score: %.4f MSE (%.4f RMSE)',
    trainScore,
    sqrt(trainScore))

sprintf(
    'Test Score: %.4f MSE (%.4f RMSE)',
    testScore,
    sqrt(testScore))

trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value

df <- data.frame(
    index = 1:length(dataset),
    value = dataset * spread + min_value,
    type = 'raw') %>%
    rbind(
        data.frame(
            index = 1:length(trainPredict) + look_back,
            value = trainPredict,
            type = 'train')) %>%
    rbind(
        data.frame(
            index = 1:length(testPredict) + look_back + length(train),
            value = testPredict,
            type = 'test'))

ggplot(data = df) +
    geom_line(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_point(
        mapping = aes(
            x = index,
            y = value,
            color = type)) +
    geom_vline(
        xintercept = length(train) + 0.5) +
    theme_economist() +
    scale_color_economist()
[1] "Train Score: 1150.3215 MSE (33.9164 RMSE)"
[1] "Test Score: 5795.0083 MSE (76.1250 RMSE)"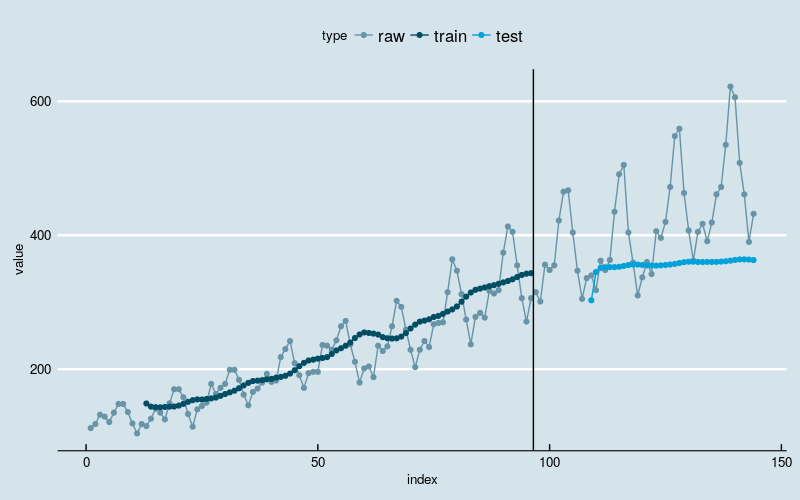

圖6

圖6

幾乎是最差的結果。訓練部分網路僅僅能夠識別出了數據的大體增長趨勢，但在測試部分，網路看起來把學習到的東西全“忘記”了。

總結

尺有所短，寸有所長。

儘管更加複雜先進 LSTM 網路在其他領域取得了出色的表現，但在這個具體的例子上，表現卻不如更簡單的多層感知機回歸。反思問題的原因：

  1. 簡單模型在“小樣本 + 簡單模式”的數據集上更容易獲得穩健的結果；
  2. 目前使用的 LSTM 網路結構可能不適應當前的問題。
  3. 解決問題的方法論——回歸，可能對當前的問題是不合適的。

擴展閱讀


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • C++強制類型轉換
    static_cast 任何具有明確定義的類型轉換，只要不包含底層const，都可以使用static_cast。例如： int i = 3, j = 2; double slope = static_cast<double>(i) / j; static_cast還可以用於把void*轉換成別的類型 ...
  • pycharm2017.3.3永久激活（轉載）
    pycharm是很強大的開發工具，但是每次註冊著實讓人頭疼。網路上很多註冊碼、註冊伺服器等等、但都只是一年或者不能用；為次有如下解決方案。親測有效！！！ 如果想讓pycharm永久被激活，比如截止日到2099-12-31;這應該算是永久激活了吧； step1: 下載jar包： 此jar包的目的就是讓 ...
  • 為什麼繼續選擇DELPHI?
    已經鑽DELPHI很深了，當然現在DELPHI是過了最輝煌的時代。但為什麼要繼續下去，而不轉向其它的?這是不是死腦筋？ 我看了一下C#的LINQ的產生，然後又被實體框架所代替。思考了一下： 1）LINQ的確是有好處，但是所用的場景又不多，這樣就會變得很雞肋。所以說學新的東西，有時對自己來說不一定有相 ...
  • python之Django rest_framework總結
    一、rest api a、api就是介面 如： - http://www.oldboyedu.com/get_user/ - http://www.oldboyedu.com/get_users/ b、api的兩個用途 1、為別人提供服務 2、前後端分離 二、restful a、--字面意思：表徵狀 ...
  • CSP201709-1：打醬油
    引言：CSP（http://www.cspro.org/lead/application/ccf/login.jsp）是由中國電腦學會（CCF）發起的"電腦職業資格認證"考試，針對電腦軟體開發、軟體測試、信息管理等領域的專業人士進行能力認證。認證對象是從事或將要從事IT領域專業技術與技術管理人 ...
  • Laravel (5.5.33) 載入過程---instance方法（三)
    在bootstrap/app.php 實例化 vendor/laravel/framework/src/Illuminate/Foundation/Application.php類 該類的魔術方法 查看註冊 app 和container到 instances數組中 查看今天主要的方法 instanc ...
  • Python_學習經驗總結2018.2.17【持續更新】
    1.準備 準備電腦 和 分區 1.準備配置稍高的電腦（後後期需要裝虛擬機），解析度1920 1080 2.分區： C→系統 D→Project E→軟體安裝盤 F→其他 準備編輯器 1.Sublime Text + VsCode + Pycharm 配置方法在網上找 2.學習中間 不懂的單詞隨時查 ...
  • 180217_JAVA學習_TreeSet中存放含多個String的類並設置排序規則
    有Person類如下： 有main如下： 由於TreeSet為可排序集合，所以要為存放對象（Person）指定排序規則。 排序規則：ASC（升序），age > address > name故重寫Person的compareTo()： 註：若要DESC排序： 1、age比較中交換1/-1； 2、add ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類