Python之演算法

一、什麼演算法

演算法：一個計算過程，解決問題的方法

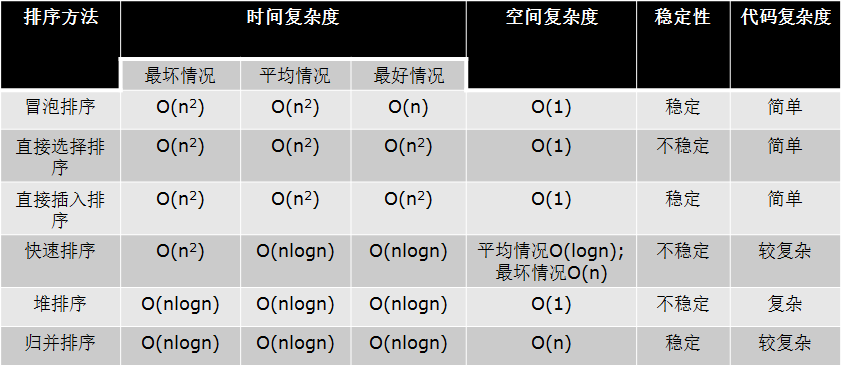
二、時間複雜度

看代碼：

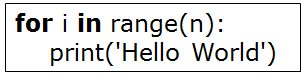
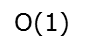
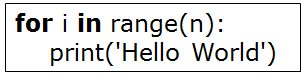
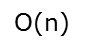
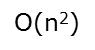
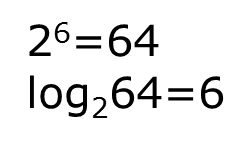
Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n^{2)＜O(n2logn)< Ο(n}3）＜…＜Ο(2^n)＜Ο(n!)

三、空間複雜度

空間複雜度:用來評估演算法記憶體占用大小的一個式子

複習：遞歸

遞歸的兩個特點：

     調用自身

     結束條件

看下麵幾個函數

def func1(x):
     print(x)
     func1(x-1)

def func2(x):
     if x>0:
          print(x)
          func2(x+1)

def func3(x):
     if x>0:
          print(x)
          func3(x-1)

def func4(x):
     if x>0:
          func4(x-1)
          print(x)

def test(n):
    if n == 0:
        print("我的小鯉魚", end='')
    else:
        print("抱著", end='')
        test(n-1)
        print("的我", end='')

test(5)

遞歸實例：漢諾塔問題

t = 0

def hanoi(n, A, B, C):
    global t
    if n > 0:
        hanoi(n-1, A, C, B)
        t += 1
        print("%s -> %s" % (A, C))
        hanoi(n-1, B, A, C)

hanoi(8,'A','B','C')
print(t)

列表查找

二分法查找 

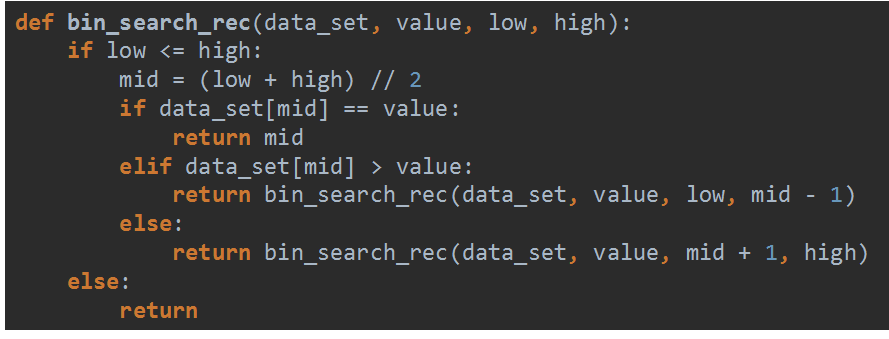
使用二分法查找來查找3

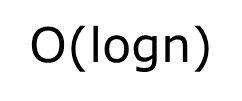
遞歸版本的二分法查找

排序Low B三人組

   冒泡排序

   選擇排序

   插入排序

演算法的關鍵點：

   有序區

   無序區

1、冒泡排序的思路

冒泡排序---優化

import random
from timewrap import *

@cal_time
def bubble_sort(li):
    for i in range(len(li) - 1):
        # i 表示趟數
        # 第 i 趟時： 無序區：(0，len(li) - i)
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

@cal_time
def bubble_sort_2(li):      #冒泡排序優化
    for i in range(len(li) - 1):
        # i 表示趟數
        # 第 i 趟時： 無序區：(0，len(li) - i)
        change = False
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                change = True
        if not change:
            return

li = list(range(10000))
# random.shuffle(li)
# print(li)
bubble_sort_2(li)
print(li)

選擇排序的思路

選擇排序代碼

import random
from timewrap import *

@cal_time
def select_sort(li):
    for i in range(len(li) - 1):
        # i 表示趟數，也表示無序區開始的位置
        min_loc = i   # 最小數的位置
        for j in range(i + 1, len(li)):
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]


li = list(range(10000))
random.shuffle(li)
print(li)
select_sort(li)
print(li)

插入排序思路

插入排序代碼

import random
from timewrap import *

@cal_time
def insert_sort(li):
    for i in range(1, len(li)):
        # i 表示無序區第一個數
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序區最後位置
        while li[j] > tmp and j >= 0:
            #迴圈終止條件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp


li = list(range(10000))
random.shuffle(li)
print(li)
insert_sort(li)
print(li)

排序LOW B三人組------小結

快速排序：

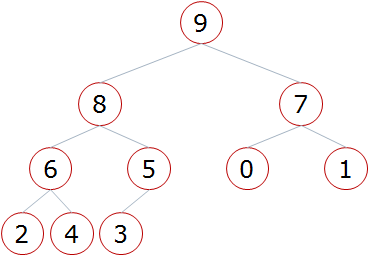
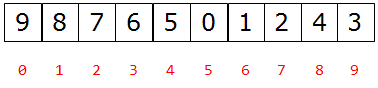
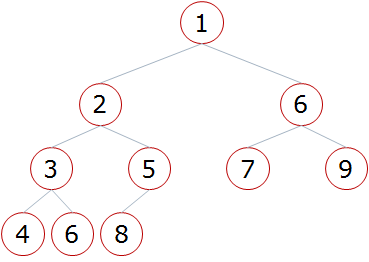
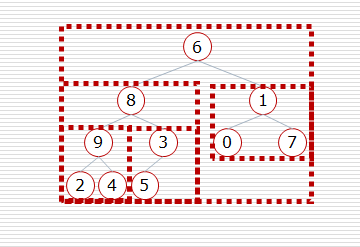
from timewrap import *
import random

def _sift(li, low, high):
    """
    :param li:
    :param low: 堆根節點的位置
    :param high: 堆最有一個節點的位置
    :return:
    """
    i = low  # 父親的位置
    j = 2 * i + 1  # 孩子的位置
    tmp = li[low]  # 原省長
    while j <= high:
        if j + 1 <= high and li[j + 1] > li[j]:  # 如果右孩子存在並且右孩子更大
            j += 1
        if tmp < li[j]:  # 如果原省長比孩子小
            li[i] = li[j]  # 把孩子向上移動一層
            i = j
            j = 2 * i + 1
        else:
            li[i] = tmp  # 省長放到對應的位置上(幹部)
            break
    else:
        li[i] = tmp  # 省長放到對應的位置上(村民/葉子節點)


def sift(li, low, high):
    """
    :param li:
    :param low: 堆根節點的位置
    :param high: 堆最有一個節點的位置
    :return:
    """
    i = low         # 父親的位置
    j = 2 * i + 1   # 孩子的位置
    tmp = li[low]   # 原省長
    while j <= high:
        if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子存在並且右孩子更大
            j += 1
        if tmp < li[j]: # 如果原省長比孩子小
            li[i] = li[j]  # 把孩子向上移動一層
            i = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp


@cal_time
def heap_sort(li):
    n = len(li)
    # 1. 建堆
    for i in range(n//2-1, -1, -1):
        sift(li, i, n-1)
    # 2. 挨個出數
    for j in range(n-1, -1, -1):    # j表示堆最後一個元素的位置
        li[0], li[j] = li[j], li[0]
        # 堆的大小少了一個元素 （j-1）
        sift(li, 0, j-1)


li = list(range(10000))
random.shuffle(li)
heap_sort(li)
print(li)

# li=[2,9,7,8,5,0,1,6,4,3]
# sift(li, 0, len(li)-1)
# print(li)

import heapq, random

li = [5,8,7,6,1,4,9,3,2]

heapq.heapify(li)
print(heapq.heappop(li))
print(heapq.heappop(li))

def heap_sort(li):
    heapq.heapify(li)
    n = len(li)
    new_li = []
    for i in range(n):
        new_li.append(heapq.heappop(li))
    return new_li

li = list(range(10000))
random.shuffle(li)
# li = heap_sort(li)
# print(li)

print(heapq.nlargest(100, li))

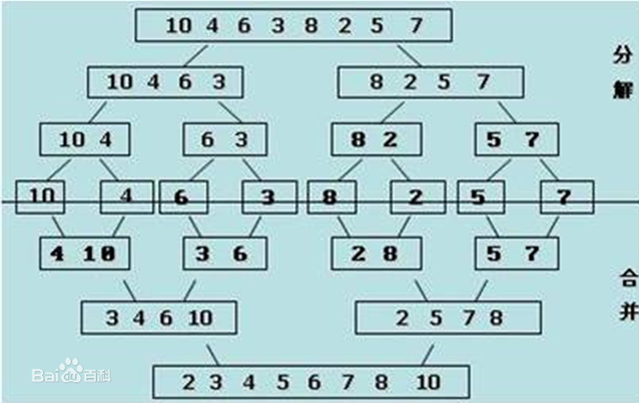
import random
from timewrap import *
import copy
import sys


def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp


def _merge_sort(li, low, high):
    if low < high:  # 至少兩個元素
        mid = (low + high) // 2
        _merge_sort(li, low, mid)
        _merge_sort(li, mid+1, high)
        merge(li, low, mid, high)
        print(li[low:high+1])


def merge_sort(li):
    return _merge_sort(li, 0, len(li)-1)


li = list(range(16))
random.shuffle(li)
print(li)
merge_sort(li)

print(li)

希爾排序

插入排序
def insert_sort(li):
    for i in range(1, len(li)):
        # i 表示無序區第一個數
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序區最後位置
        while li[j] > tmp and j >= 0:
            #迴圈終止條件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp

比較


希爾排序
def shell_sort(li):
    d = len(li) // 2
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]
                j -= d
            li[j+d] = tmp
        d = d >> 1

計數排序

# 0 0 1 1 2 4 3 3 1 4 5 5
import random
import copy
from timewrap import *

@cal_time
def count_sort(li, max_num = 100):
    count = [0 for i in range(max_num+1)]
    for num in li:
        count[num]+=1
    li.clear()
    for i, val in enumerate(count):
        for _ in range(val):
            li.append(i)

@cal_time
def sys_sort(li):
    li.sort()

li = [random.randint(0,100) for i in range(100000)]
li1 = copy.deepcopy(li)
count_sort(li)
sys_sort(li1)

from collections import deque

f = open('test.txt','r')

q = deque(f, 3)

for line in q:
    print(line)