K：樹與二叉樹

相關介紹:

 樹（英語：tree）是一種抽象數據類型（ADT）或是作這種抽象數據類型的數據結構，用來模擬具有樹狀結構性質的數據集合。它是由n（n>0）個有限節點組成的一個具有層次關係的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹，也就是說它是根朝上，而葉朝下的。樹形結構中數據元素之間具有一對多的邏輯關係，它反映了數據元素之間的層次關係，一個數據元素可以有多個後繼，但最多只能有一個前驅。二叉樹是樹裡面的一個特殊形態，每個節點最多只有兩個分支(不存在分支度大於2的節點)。通常分支被稱作“左子樹”和“右子樹”。二叉樹的分支具有左右次序，不能顛倒。

以下介紹樹相關的知識點:

1. 樹的定義：樹是由n(n>=0)個節點所構成的有限集合，當n=0時，稱之為空樹；當n>0時，n各節點，滿足以下的情況:

   • 有且僅有一個稱之為根的節點。
   • 其餘節點可分為m(m>=0)個互不相交的有限集合，且每一個集合又構成一棵樹，這棵樹稱為根節點的子樹。

2. 樹的表示方法：樹形表示法(最為常用)、文氏圖表示法、凹入圖表示法、廣義表示法。圖1.1展示了樹的這四種表示方法。

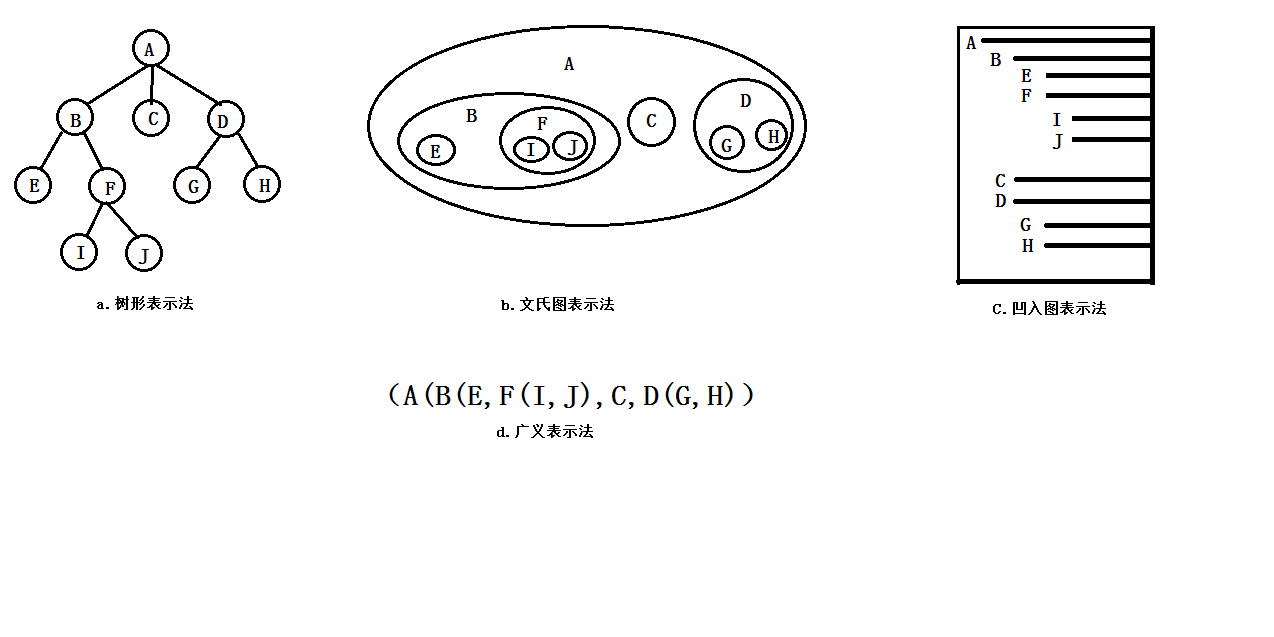
1. 樹的常用術語：

   • 樹的節點：由一個數據元素及關聯其子樹的邊所組成

   • 節點的路徑：從根節點到該節點所經歷的分支和節點的順序排列

   • 路徑的長度：指節點路徑中所包含的分支數，也就是路徑的節點數目減一。例如有一路徑A->B->C->D,則其路徑長度為3

   • 節點的度：該節點擁有的子樹的數目

   • 樹的度：樹中所有節點的度的最大值

   • 葉節點(終端節點)：樹中度為0的節點

   • 分支節點(非終端節點、內部節點)：樹中度不為0的節點。在樹中，除了葉節點外的所有節點都是分支節點

   • 孩子節點(子節點)：一個節點的孩子節點是指這個節點的子樹的根節點

   • 雙親節點(父節點)：若樹中某個節點有孩子節點，則這個節點就稱為孩子節點的雙親節點。雙親節點和孩子節點也稱為是具有互為前驅和後繼關係的節點

   • 子孫節點：一個節點的子孫節點是指這個節點的所有子樹中的任意節點

   • 祖先節點：一個節點的祖先節點是指該節點的路徑中除此節點之外的所有節點

   • 兄弟節點：具有同一雙親的節點稱為兄弟節點

   • 節點的層次：假設根節點的層次為0，則其它節點的層次是雙親節點的 層次數加一

   • 樹的深度：樹中所有節點層次數的最大值加一

   • 有序樹：樹中各節點的所有子樹之間從左到右有嚴格的次序關係

   • 無序樹：與有序樹相反，無序樹是指樹中各節點的所有子樹之間沒有嚴格的次序關係

   • 森林：由m(m>=0)棵互不相交的樹所構成的集合

 二叉樹是一棵特殊的樹，它的每個節點最多只有兩棵子樹，並且這兩棵子樹也是二叉樹，由於二叉樹中的兩棵子樹有左右之分，為此，二叉樹是有序樹。

1. 二叉樹的基本概念：二叉樹是由n(n>=0)個節點所構成的有限集合。當n=0時，這個集合為空，此時的二叉樹為空樹；當n>0時，這個集合是由一個根節點和兩個互不相交的分別稱為左子樹和右子樹的二叉樹所構成。

2. 滿二叉樹：如果在一棵二叉樹中，它的所有節點或者是葉節點，或者是左、右子樹都非空，並且所有葉節點都在同一層上，則稱這棵二叉樹為滿二叉樹。

3. 完全二叉樹：如果在一棵具有n個節點的二叉樹中，它的邏輯結構與滿二叉樹的前n個節點的邏輯結構相同，則稱這樣的二叉樹為完全二叉樹。完全二叉樹其只允許缺少的葉節點在右半部分，而不允許在左半部分。下圖1.2展示了滿二叉樹和完全二叉樹，完全二叉樹與非完全二叉樹之間的區別。

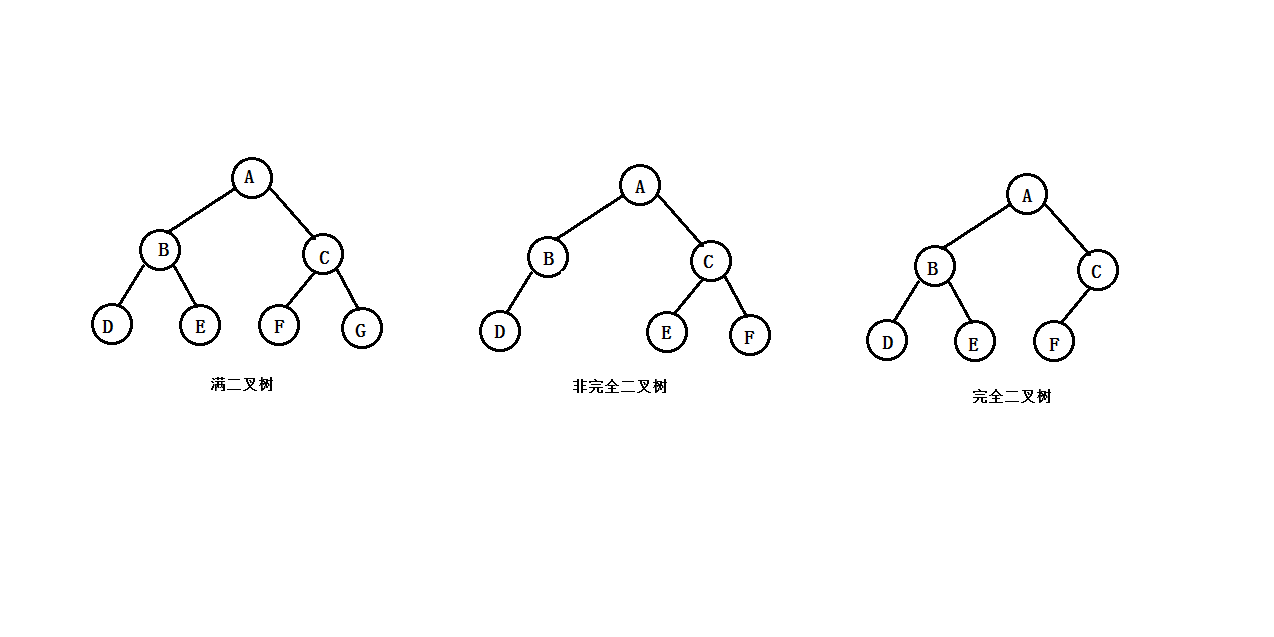
1. 二叉樹的性質：

   • 在二叉樹的第i層上至多有\(2^{i}\)個節點(i>=0)

   • 深度為h(h>=0)的二叉樹上至多含有\(2^{h}-1\)個節點

   • 對於任何一棵二叉樹，若其葉節點的個數為N0，度數為2的節點的個數為N2，則有N0=N2+1。證明過程如下：

   設二叉樹中度為1的節點個數為n1，二叉樹的節點總數為n，則有:
   n=n0+n1+n2
   
   再設二叉樹中具有e個分支，而度為1的節點是引出一個分支，度為2的節點是引出兩個分支，則有:
   e=n1+n2*2
   
   又因為在二叉樹中，除根節點外，每個節點均對應一個進入它的分支，所以有:
   n=e+1
   
   整合以上各式，得到n0=n2+1

   • 具有n個節點的完全二叉樹的深度為\(\lfloor log_{2}N \rfloor+1\)或者\(\lceil log_{2}(N+1) \rceil\)

   • 若對含n個節點的完全二叉樹從上到下，且從左到右進行0至n-1的編號，則對完全二叉樹中任意一個編號為i的節點，有:

     1. 若i=0,則該節點是二叉樹的根，無雙親；否則，編號為\(\lfloor \frac{i-1}{2} \rfloor\)的節點為其雙親節點

     2. 若2i+1>=n，則該節點無左孩子節點，否則，編號為2i+1的節點為其左孩子節點

     3. 若2i+2>=n，則該節點無右孩子節點，否則，編號為2i+2的節點為其右孩子節點

樹與二叉樹的區別：

 從二叉樹的定義中可以看出，二叉樹與樹有著很大的不同，它們的區別在於:

1. 樹中的每個節點可以有多棵子樹，而二叉樹中的每個節點最多只能有2棵子樹
2. 樹中的子樹是不分順序的，而二叉樹中的子樹有嚴格的左、右之分
3. 二叉樹與度小於等於2的樹不同。在二叉樹中允許某些節點只有右子樹而沒有左子樹，而在樹中，一個節點若沒有第一棵子樹，則它就不可能有第二棵子樹的存在。

回到目錄|·(工)·）