Trie樹與AC自動機作為現階段的學習中個人應有的常識，AC自動機形象的來講就是在Trie樹上跑的一個KMP。由此，我們就先來談一談Trie樹。(有圖) 1. Trie樹又稱單詞查找樹，字典樹，一般用於字元串的匹配。它利用公共的字元串首碼進行查詢，減少了無謂的操作，是空間換時間的經典演算法。舉例： ...

Trie樹與AC自動機

作為現階段的學習中個人應有的常識，AC自動機形象的來講就是在Trie樹上跑的一個KMP。由此，我們就先來談一談Trie樹。(有圖)

1. Trie樹

又稱單詞查找樹，字典樹，一般用於字元串的匹配。它利用公共的字元串首碼進行查詢，減少了無謂的操作，是空間換時間的經典演算法。舉例：

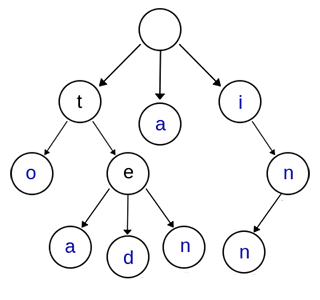
此圖包含了{"to", "tea", "ted", "ten", "a", "i", "in", "inn"}這些字元串。

Trie樹的基本性質可以歸納為：

根節點不包含字元，除根節點意外每個節點只包含一個字元。
從根節點到某一個節點，路徑上經過的字元連接起來，為該節點對應的字元串。
每個節點的所有子節點包含的字元串不相同。

Trie樹有兩個基本操作，一為插入，二為刪除，且兩者複雜度均為$O(len)$（其中$len = $ 字元串長度）。

我們以對五個串aaaa,abb,aabbb,baa,bab的操作進行說明。

1.基本操作

1.插入

1. 插入`aaaa`

首先插入串aaaa。對樹中沒有的節點進行新建，連接。結果：

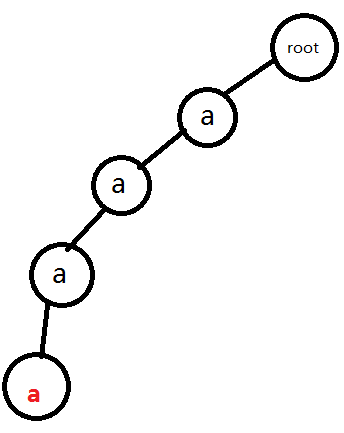
example1

對，就是這樣的簡單插入。（圖中紅色字母代表一個單詞的結尾）

2. 插入`abb`

再插入串abb。在插入時，已有的節點直接走過去，沒有的就插入再走過去。結果：

1.插入`a`

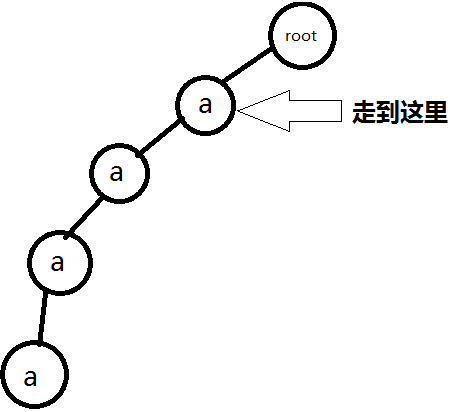
example2

2.插入`b`

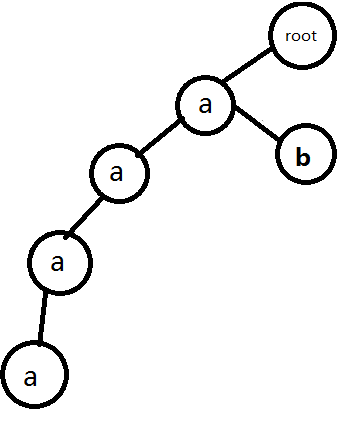
example3

3.再插入`b`

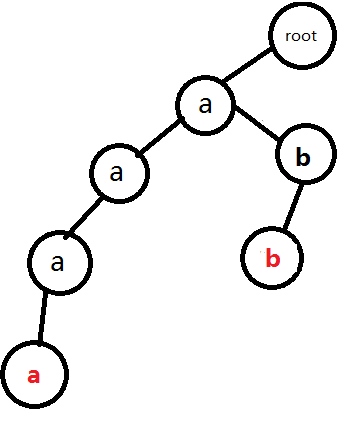
example4

完成。

3.插入`aabbb`

不再贅述，此操作請認真思考。結果：

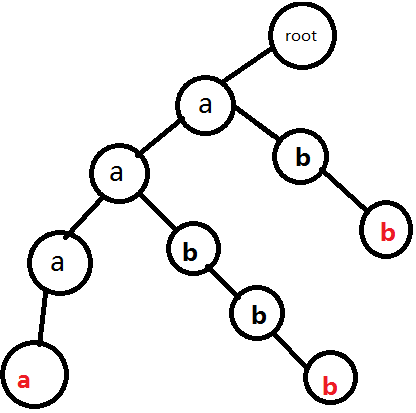
example5

4.插入`baa`

因為根節點的兒子中沒有b，所以我們要在根節點後掛上一個b。其餘的新建與第一個串一樣。結果：

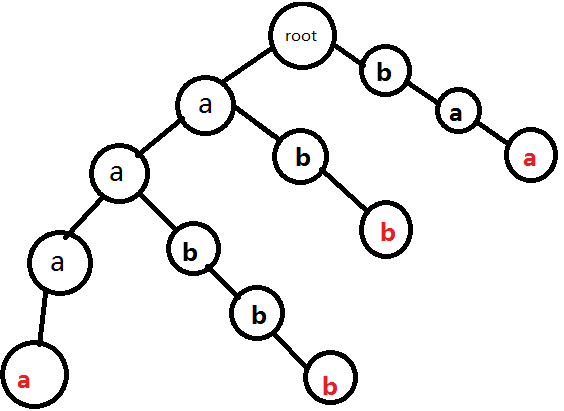
example5

5.插入`bab`

與第二個串相同。結果：

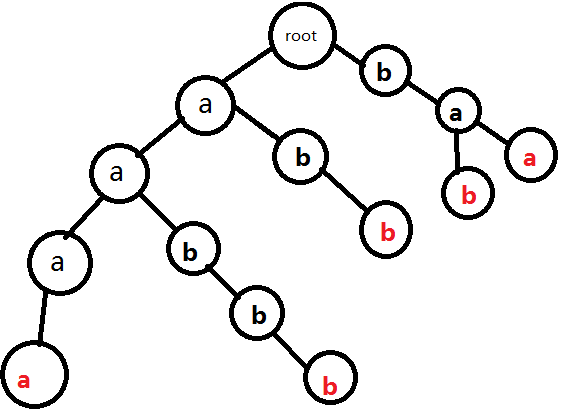
example6

結束。

2.查詢

為了避免冗餘，我們用簡單的幾張圖片表示過程。以串aabbb為例：

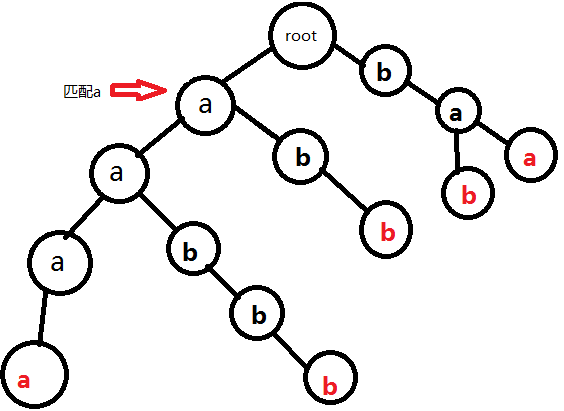
example7

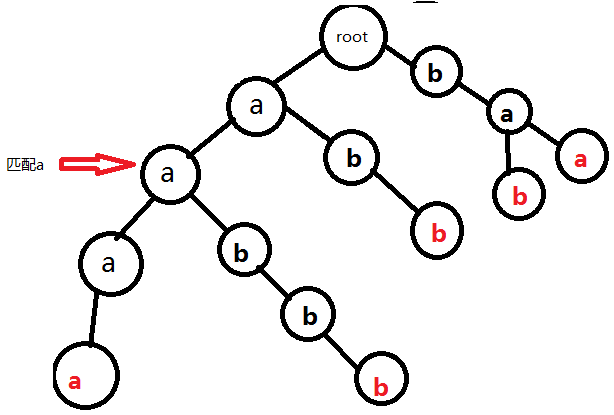
example8

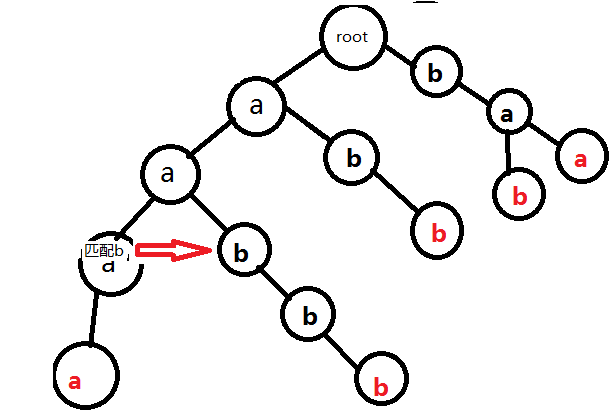
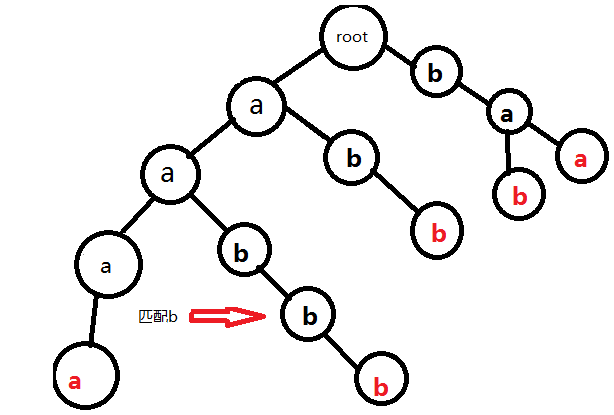
example9

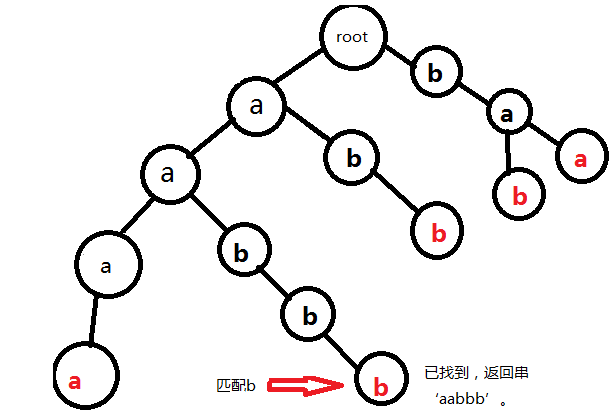
example10

完成。

簡單的操作就是這些。但在實際應用中，往往不只是單純返回一個串，更常用的是返回此處是否有串，或是串的個數，抑或狀態。下麵我們以幾個題目做例子。

2.題目

1.洛谷P2580 於是他錯誤的點名開始了

大意：

給定$n$個字典串，再對$m$個模式串進行匹配，若匹配到，輸出$O$，未匹配到，輸出$WRONG$，若匹配到且之前已經被匹配，輸出$REPEAT$。

解：真的是很基本的Trie樹的題，此題在這裡是做代碼範例用途。詳細解釋見代碼。（不要在意這神奇的代碼風格）

#include <iostream>
#define re register
const int MAXN = 1000001;
struct Trie{                //定義Trie樹的結構，因為當前節點後可能會有26個小寫字母，也就是26個後繼，所以數組開26大小。
    int next[26];
    bool exist, repeat;     //exist：是否是字元串結尾（當前位置是否有字元串）；repeat：此字元串是否被查詢過。
}a[MAXN];
int top, n, m;
std::string str;
inline void Trie_insert() {
    int iter(0), now(0), tmp(0);        //iter：指向字元；now：指向節點。此兩者起指針作用。
    for (iter; str[iter]; ++iter) {     //遍歷當前插入字元串。
        tmp = str[iter] - 'a';          //將當前字母用數字表示。
        if(!a[now].next[tmp]) a[now].next[tmp] = ++top;     //如果當前節點沒有代表該字母的後繼，則新建節點。
        now = a[now].next[tmp];         //將指針向後移。
    }
    a[now].exist = true;                //當前節點代表字元串結尾。
    return ;
}
inline int Trie_search() {
    int iter(0), now(0), tmp(0);
    for (iter; str[iter]; ++iter) {     //遍歷當前查詢字元串。
        tmp = str[iter] - 'a';          //與上方操作相同。
        if(!a[now].next[tmp]) return 0; //如果當前節點沒有代表該字母的後繼，則說明查詢失敗，返回零。
        now = a[now].next[tmp];         //指針後移。
    }
    return a[now].exist ? (!a[now].repeat ? (a[now].repeat = 1) : 2) : 0;
  /*
        相當於：
        if(a[now].exist) {              //判斷是否存在
            if(a[now].repeat) return 2; //判斷是否查詢過
            else {a[now].repeat = 1; return 1;}
        }
        else return 0;
  */
}
int main() {
    std::ios::sync_with_stdio(false);
    std::cin >> n;
    for (re int i = 1; i <= n; ++i) std::cin >> str, Trie_insert();
    std::cin >> m;
    for (re int i = 1; i <= m; ++i) {
        std::cin >> str;
        switch(Trie_search()) {     //得到查詢的返回值。若是0，說明匹配未成功；是1，說明匹配成功；是2，說明匹配成功，且重覆匹配。
            case (0): {
                std::cout << "WRONG\n";
                break;
            }
            case (1): {
                std::cout << "OK\n";
                break;
            }
            default: {
                std::cout << "REPEAT\n";
            }
        }
    }
    return 0;
}

就是這樣。

2.洛谷P2922 [USACO08DEC] 秘密消息Secret Message

大意：

給定$M(1 \leqslant M \leqslant 50000)$個字典串，第$i$個字典串有$Bi(1 \leqslant Bi \leqslant 10000)$位。再給定N($1 \leqslant N \leqslant 50000$)個模式串，第$i$個模式串有$Cj$($1 \leqslant Cj \leqslant 10000$)位 ($(\sum_{i = 1}^{M}Bi + \sum_{j = 1}^{N}Cj) \leqslant 500000$)。對每個模式串$j$，求有多少串與當前模式串有相同首碼。(包括長度長於，等於與小於模式串的字典串)

解：在插入沿途做經過的標記，標記當前字母被幾個字元串經過。在查詢時$ans$加上經過字母上的結束標記。查詢結束時，如果是走到字典串結尾而結束，$ans$加上結束標記，直接退出；如果是走到模式串結尾而結束，$ans$則不加結束標記，而是要加上經過標記，然後退出。

前面的加結束標記好理解，但為什麼字典串比模式串長時要加經過標記呢？因為字典串比模式串長，說明字典串以模式串為首碼，按題意求有多少串與當前模式串有相同首碼，又因為經過標記正好代表這些串的個數，當然要用經過標記了。

這一道題思維量並不大，也算一道入門題。

#include <cctype>
#include <cstdio>
const int N = 10000;
struct Node{
    int next[2], exist, passby;         //exist：結束標記；passby：經過標記。
}cow[500010];
int m, n, b, j, tot, top;
bool fl(0);
char buf[N], *p = buf, *end = buf;
inline char Get_char() {
    if(p == end) {
        if(feof(stdin)) return (0);
        p = buf; end = buf + fread(buf, 1, N, stdin);
    }
    return *(p++);
}
inline void Get_int(int &x) {
    x = 0; char c(0);
    while (!isdigit(c = Get_char()));
    do {x = (x << 1) + (x << 3) + (c ^ 48);}
    while (isdigit(c = Get_char()));
    return ;
}
inline void Insert(int lent) {
    int now(0), c(0);
    for (int i = 1; i <= lent; ++i) {
        Get_int(c);
        if(!cow[now].next[c]) cow[now].next[c] = ++top;
        cow[cow[now].next[c]].passby++;         //普通插入，只不過多了經過標記。
        now = cow[now].next[c];
    }
    cow[now].exist++;
    return ;
}
inline void Query(int lent) {
    int now(0), c(0); tot = 0; fl = false; int i;
    for (i = 1; i <= lent; ++i) {
        Get_int(c);
        if(!cow[now].next[c]) {fl = true; break;}   //標記第一種情況，即字典串比模式串短。
        now = cow[now].next[c];
        tot += cow[now].exist;                      //加結束標記。
    }
    for (i = i + 1; i <= lent; ++i)
        Get_int(c);
    if(fl) {printf("%d\n", tot);}
    else {printf("%d\n", tot - cow[now].exist + cow[now].passby);}  //第二種情況，即字典串比模式串長，則減掉之前加上的結束標記，加上經過標記。
    return ;
}
int main() {
    Get_int(m); Get_int(n);             //不要在意快讀。
    for (int i = 1; i <= m; ++i) {
        Get_int(b); Insert(b);          //插入操作。
    }
    for (int i = 1; i <= n; ++i) {
        Get_int(j); Query(j);           //查詢操作。
    }
    return 0;
}

Trie樹與AC自動機（未完成）

Trie樹與AC自動機