演算法是電腦處理信息的本質,因為電腦程式本質上是一個演算法來告訴電腦確切的步驟來執行一個指定的任務。一般地,當演算法在處理信息時,會從輸入設備或數據的存儲地址讀取數據,把結果寫入輸出設備或某個存儲地址供以後再調用。 演算法是獨立存在的一種解決問題的方法和思想。 一道題引入如果 a+b+c=1000,且 ...
演算法是電腦處理信息的本質,因為電腦程式本質上是一個演算法來告訴電腦確切的步驟來執行一個指定的任務。一般地,當演算法在處理信息時,會從輸入設備或數據的存儲地址讀取數據,把結果寫入輸出設備或某個存儲地址供以後再調用。
演算法是獨立存在的一種解決問題的方法和思想。
一道題引入如果 a+b+c=1000,且 a^2+b^2=c^2(a,b,c 為自然數),如何求出所有a、b、c可能的組合?
解決思路1:

import time start_time = time.time() # 註意是三重迴圈 for a in range(0, 1001): for b in range(0, 1001): for c in range(0, 1001): if a**2 + b**2 == c**2 and a+b+c == 1000: print("a, b, c: %d, %d, %d" % (a, b, c)) end_time = time.time() print("elapsed: %f" % (end_time - start_time)) print("complete!") ############################# 運行結果: a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 214.583347 complete!枚舉法
演算法的五大特性:
1.輸入: 演算法具有0個或多個輸入;
2.輸出: 演算法至少有1個或多個輸出;
3.有窮性: 演算法在有限的步驟之後會自動結束而不會無限迴圈,並且每一個步驟可以在可接受的時間內完成;
4.確定性:演算法中的每一步都有確定的含義,不會出現二義性;
5.可行性:演算法的每一步都是可行的,也就是說每一步都能夠執行有限的次數完成。
根據上面的枚舉法可以看出,多層嵌套的for迴圈是非常消耗時間的,類似於笛卡兒積的增長。我們完全可以把c的迴圈解除,根據a+ b+c=1000,c=1000- a - b。
我們的代碼可以改成:

import time start_time = time.time() # 註意是兩重迴圈 for a in range(0, 1001): for b in range(0, 1001-a): c = 1000 - a - b if a**2 + b**2 == c**2: print("a, b, c: %d, %d, %d" % (a, b, c)) end_time = time.time() print("elapsed: %f" % (end_time - start_time)) print("complete!") ########################### 運行結果: a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 0.182897 complete!修改代碼
從運行時間上來看,第二種方法顯然效率要高很多。我們使用大o法來確定演算法的效率。
我們假定電腦執行演算法每一個基本操作的時間是固定的一個時間單位,那麼有多少個基本操作就代表會花費多少時間單位。算然對於不同的機器環境而言,確切的單位時間是不同的,但是對於演算法進行多少個基本操作(即花費多少時間單位)在規模數量級上卻是相同的,由此可以忽略機器環境的影響而客觀的反應演算法的時間效率。
怎麼解釋大O法:“大O記法”:對於單調的整數函數f,如果存在一個整數函數g和實常數c>0,使得對於充分大的n總有f(n)<=c*g(n),就說函數g是f的一個漸近函數(忽略常數),記為f(n)=O(g(n))。也就是說,在趨向無窮的極限意義下,函數f的增長速度受到函數g的約束,亦即函數f與函數g的特征相似。
時間複雜度:假設存在函數g,使得演算法A處理規模為n的問題示例所用時間為T(n)=O(g(n)),則稱O(g(n))為演算法A的漸近時間複雜度,簡稱時間複雜度,記為T(n)。
簡單來說就是大O法就是忽略常數c,它認為3*n**2和100*n**2屬於同一個量級,如果兩個演算法處理同樣規模實例的代價分別為這兩個函數,就認為它們的效率“差不多”,都為n**2級。
時間複雜度的幾條基本計算規則,
基本操作,即只有常數項,認為其時間複雜度為O(1),
順序結構,時間複雜度按加法進行計算,
迴圈結構,時間複雜度按乘法進行計算,
分支結構,時間複雜度取最大值,
判斷一個演算法的效率時,往往只需要關註操作數量的最高次項,其它次要項和常數項可以忽略,
在沒有特殊說明時,我們所分析的演算法的時間複雜度都是指最壞時間複雜度。
再回到我們最初的問題,我們第一次使用的枚舉法時間複雜度:
T(n) = O(n*n*n) = O(n**3)
第二次的演算法時間複雜度:
T(n) = O(n*n*(1+1)) = O(n*n) = O(n**2)
我們之前寫過的演算法圖解里也對大O法進行瞭解釋:
大O法的消耗時間由小到大的順序為:O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)。
timeit模塊
timeit模塊可以用來測試一小段Python代碼的執行速度。

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>) Timer是測量小段代碼執行速度的類。 stmt參數是要測試的代碼語句(statment); setup參數是運行代碼時需要的設置;相當於我們要使用time需要導入time模塊。 timer參數是一個定時器函數,與平臺有關。 timeit.Timer.timeit(number=1000000) Timer類中測試語句執行速度的對象方法。number參數是測試代碼時的測試次數,預設為1000000次。方法返回執行代碼的平均耗時,一個float類型的秒數。timeit模塊

def test1(): l = [] for i in range(1000): l = l + [i] def test2(): l = [] for i in range(1000): l.append(i) def test3(): l = [i for i in range(1000)] def test4(): l = list(range(1000)) from timeit import Timer t1 = Timer("test1()", "from __main__ import test1") print("concat ",t1.timeit(number=1000), "seconds") t2 = Timer("test2()", "from __main__ import test2") print("append ",t2.timeit(number=1000), "seconds") t3 = Timer("test3()", "from __main__ import test3") print("comprehension ",t3.timeit(number=1000), "seconds") t4 = Timer("test4()", "from __main__ import test4") print("list range ",t4.timeit(number=1000), "seconds") # ('concat ', 1.7890608310699463, 'seconds') # ('append ', 0.13796091079711914, 'seconds') # ('comprehension ', 0.05671119689941406, 'seconds') # ('list range ', 0.014147043228149414, 'seconds')生成列表的效率
所以以後千萬別寫什麼l = l + [i]增加列表了(每次都生成新列表而+=則不會生成新列表+=與extend效果一樣),因為列表本身的結構類型所以在列表的頭部或者尾部增加或刪除也是有區別的。

x = range(2000000) pop_zero = Timer("x.pop(0)","from __main__ import x") print("pop_zero ",pop_zero.timeit(number=1000), "seconds") x = range(2000000) pop_end = Timer("x.pop()","from __main__ import x") print("pop_end ",pop_end.timeit(number=1000), "seconds") # ('pop_zero ', 1.9101738929748535, 'seconds') # ('pop_end ', 0.00023603439331054688, 'seconds')列表前後插入與刪除的區別

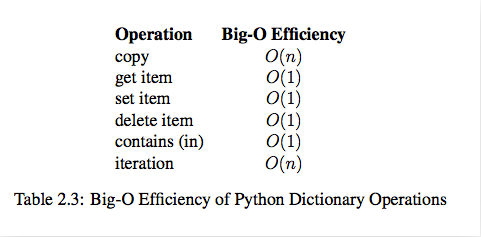
我們希望演算法解決問題的效率越快越好,於是我們就需要考慮數據究竟如何保存的問題,這就是數據結構。列表和字典就是Python內建幫我們封裝好的兩種數據結構。
數據是一個抽象的概念,將其進行分類後得到程式設計語言中的基本類型。如:int,float,char等。數據元素之間不是獨立的,存在特定的關係,這些關係便是結構。數據結構指數據對象中數據元素之間的關係。
抽象數據類型(ADT)是把數據類型和數據類型上的運算捆在一起,進行封裝。引入抽象數據類型的目的是把數據類型的表示和數據類型上運算的實現與這些數據類型和運算在程式中的引用隔開,使它們相互獨立。類似於面向對象提供api操作。




