面向對象編程 —— java實現函數求導

文章目錄 ★引子 ★求導 ★最初的想法 ★初步的想法 ★後來的想法 ★最後的想法 ★編程範式 ★結尾首先聲明一點，本文主要介紹的是面向對象（OO）的思想，順便談下函數式編程，而不是教你如何準確地、科學地用java求出函數在一點的導數。 ★引子首先，直接上一段python代碼，請大家先分析下上面代 ...

文章目錄

★引子

首先聲明一點，本文主要介紹的是面向對象（OO）的思想，順便談下函數式編程，而不是教你如何準確地、科學地用java求出函數在一點的導數。

★引子

def d(f) :
    def calc(x) :
        dx = 0.000001  # 表示無窮小的Δx
        return (f(x+dx) - f(x)) / dx  # 計算斜率。註意，此處引用了外層作用域的變數 f
    return calc  # 此處用函數作為返回值（也就是函數 f 的導數）
# 計算二次函數 f(x) = x2 + x + 1的導數
f = lambda x : x**2 + x + 1  # 先把二次函數用代碼表達出來
f1 = d(f)# 這個f1 就是 f 的一階導數啦。註意，導數依然是個函數
# 計算x=3的斜率
f1(3)
# 二階導數
f2 = d(f1)

首先，直接上一段python代碼，請大家先分析下上面代碼是用什麼方法求導的。請不要被這段代碼嚇到，你無需糾結它的語法，只要明白它的求導思路。

以上代碼引用自《為啥俺推薦 Python[4]：作為函數式編程語言的 Python》，這篇博客是促使我寫篇文章的主要原因。

博主說“如果不用 FP，改用 OOP，上述需求該如何實現？俺覺得吧，用 OOP 來求導，這代碼寫起來多半是又醜又臭。”

我將信將疑，於是就用面向對象的java試了試，最後也沒多少代碼。如果用java8或以後版本，代碼更少。

請大家思考一個問題，如何用面向對象的思路改寫這個程式。請先好好思考，嘗試編個程式再繼續往下看。

考慮到看到這個標題進來的同學大多是學過java的，下麵我用java，用面向對象的思路一步步分析這個問題。

★求導

文章開頭我已近聲明過了，本文不是來討論數學的，求導只是我用來說明面向對象的一個例子。

如果你已經忘了開頭那段代碼的求導思路，請回頭再看看，看看用python是如何求導的。

相信你只要聽說過求導，肯定一眼就看出開頭那段代碼是用導數定義求導的。

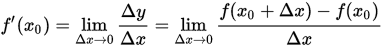
代碼中只是將無窮小Δx粗略地算做一個較小的值0.000001。

★最初的想法

//自定義函數
public class Function {
    //函數：f(x) = 3x^3 + 2x^2 + x + 1
    public double f(double x) {
        return 3 * x * x * x + 2 * x * x + x + 1;
    }
}

//一元函數導函數
public class DerivedFunction {
    //表示無窮小的Δx
    private static final double DELTA_X = 0.000001;
    //待求導的函數
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    /**
     * 獲取function在點x處的導數
     * @param x 待求導的點
     * @return 導數
     */
    public double get(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //一階導函數
        DerivedFunction derivative = new DerivedFunction(new Function());
        //列印函數在x=2處的一階導數
        System.out.println(derivative.get(2));
    }
}

先聲明一點，考慮到博客篇幅，我使用了不規範的代碼註釋，希望大家不要被我誤導。

我想只要大家好好思考了，應該至少會想到這步吧。代碼我就不解釋了，我只是用java改寫了文章開頭的那段python代碼，做了一個簡單的翻譯工作。再請大家考慮下以上代碼的問題。

剛開始，我思考這個問題想到的是建一個名為Function的類，類中有一個名為f的方法。但考慮到要每次要求新的函數導數時就得更改這個f方法的實現，明顯不利於擴展，這違背了開閉原則。

估計有的同學沒聽過這個詞，我就解釋下：”對象（類，模塊，函數等）應對擴展開放，但對修改封閉“。

於是我就沒繼續寫下去，但為了讓大家直觀的感受到這個想法，我寫這篇博客時就實現了一下這個想法。

請大家思考一下如何重構代碼以解決擴展性問題。

★初步的想法

估計學過面向對象的同學會想到把Function類改成介面或抽象類，以後每次添加新的函數時只要重寫這個介面或抽象類中的f方法，這就是面向介面編程，符合依賴反轉原則，下麵的代碼就是這麼做的。

再聲明一點，考慮到篇幅的問題，後面的代碼我會省去與之前代碼重覆的註釋，有不明白的地方還請看看上一個想法中的代碼。

//一元函數
public interface Function {
    double f(double x);
}

//自定義的函數
public class MyFunction implements Function {
    @Override
    public double f(double x) {
        return 3 * x * x * x + 2 * x * x + x + 1;
    }
}

public class DerivedFunction {
    private static final double DELTA_X = 0.000001;
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    public double get(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //一階導函數：f'(x) = 9x^2 + 4x + 1
        DerivedFunction derivative = new DerivedFunction(new MyFunction());
        System.out.println(derivative.get(2));
    }
}

我想認真看的同學可能會發現一個問題，我的翻譯做的還不到位，開頭那段python代碼還可以輕鬆地求出二階導函數（導數的導數），而我的代碼卻不行。

其實只要稍微修改以上代碼的一個地方就可以輕鬆實現求二階導，請再思考片刻。

★後來的想法

當我寫出上面的代碼時，我感覺完全可以否定“用 OOP 來求導，這代碼寫起來多半是又醜又臭”的觀點。但還不能求二階導，我有點不甘心。

於是我就動筆，列了一下用定義求一階導和求二階導的式子，想了想兩個式子的區別與聯繫，突然想到導函數也是函數。

DerivedFunction的get方法和Function的f方法的參數和返回值一樣，DerivedFunction可以實現Function介面，於是產生了下麵的代碼。

public interface Function {
    double f(double x);
}

public class DerivedFunction implements Function {
    private static final double DELTA_X = 0.000001;
    private Function function;

    public DerivedFunction(Function function) {
        this.function = function;
    }

    @Override
    public double f(double x) {
        return (function.f(x + DELTA_X) - function.f(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        Function f1 = new DerivedFunction(new Function() {
            @Override
            public double f(double x) {
                return 3 * x * x * x + 2 * x * x + x + 1;
            }
        });
        System.out.println(f1.f(2));
        //二階導函數：f''(x) = 18x + 4
        Function f2 = new DerivedFunction(f1);
        //列印函數f(x) = 3x^3 + 2x^2 + x + 1在x=2處的二階導數
        System.out.println(f2.f(2));
    }
}

考慮到有的同學沒學過java8或以上版本，以上代碼沒有用到java8函數式編程的新特性。

如果你接觸過java8，請考慮如何改寫以上代碼，使其更簡潔。

★最後的想法

public class DerivedFunction implements Function<Double, Double> {
    private static final double DELTA_X = 0.000001;
    private Function<Double, Double> function;

    public DerivedFunction(Function<Double, Double> function) {
        this.function = function;
    }

    @Override
    public Double apply(Double x) {
        return (function.apply(x + DELTA_X) - function.apply(x)) / DELTA_X;
    }
}

public class Main {
    public static void main(String[] args) {
        //列印函數在x=2處的二階導
        System.out.println(new DerivedFunction(new DerivedFunction(x -> 3 * x * x * x + 2 * x * x + x + 1)).apply(2.0));
    }
}

之前幾個想法為了擴展Function介面，使用了外部類、匿名類的方式，其實也可以用內部類。而這在這裡，我用了lambda表達式，是不是更簡潔了。

這裡用的Function介面用的是jdk自帶的，我們不需要自己定義了。因為這是一個函數式介面，我們可以用lambda方便地實現。後來發現，其實這裡用UnaryOperator這個介面更恰當。

現在大家有沒有發現，用java、用OOP也可以非常簡潔地實現求導，並不比開頭的那段python代碼麻煩很多。

★編程範式

在我看來，編程範式簡單來說就是編程的一種模式，一種風格。

我先介紹其中的三個，你差不多就知道它的含義了。

◇面向對象程式設計（OOP）

看到這裡的同學應該對面向對象有了更直觀的認識。在面向對象編程中，萬物皆對象，抽象出類的概念。基本特性是封裝、繼承、多態，認識不深的同學可以再去我之前的代碼中找找這三個特性。

我之前還介紹了面向對象的幾個原則：開閉原則、依賴反轉原則。其他還有單一職責原則、里氏替換原則、介面隔離原則。這是面向對象的5個基本原則，合稱SOLID。

◇函數編程語言（FP）

本文開頭那段代碼用的就是python函數式編程的語法，後來我又用java8函數式編程的語法翻譯了這段代碼。

相信你已經直觀地感受到它的簡潔，以函數為核心，幾行代碼就解決了求導的問題。

◇過程式編程（Procedural programming）

大概學過編程都學過C，C語言就是一種過程式編程語言。在我看來，過程式編程大概就是為了完成一個需求，像記流水帳一樣，平鋪直敘下去。

★結尾

由於本人初學java，目前只能想到這麼多。如果大家有更好的想法或者覺的我上面說的有問題，歡迎評論，望各位不吝賜教。

這是我的第一篇技術博客，但願我說清楚了面向對象。如果對你有幫助，請點個贊或者評論下，給我點繼續創作的動力。