0.要求 用戶點擊A單元格作為起始點,點擊B單元格最為終止點,要根據A、B兩個點算出四個邊界值,用來組成出一個矩形。 上圖紅色為終止點,綠色為起始點。 1.演算法 關鍵點1:合併單元格是通過rowspan,colspan來實現,意味一個單元格代替多個單元格,演算法中計算出的單元格位置需要與在視圖中看到的 ...
0.要求
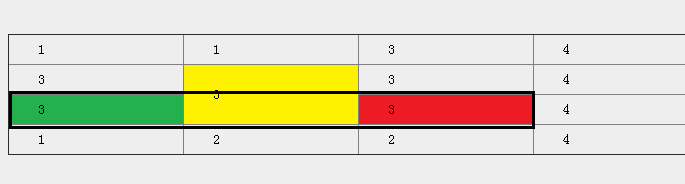
用戶點擊A單元格作為起始點,點擊B單元格最為終止點,要根據A、B兩個點算出四個邊界值,用來組成出一個矩形。
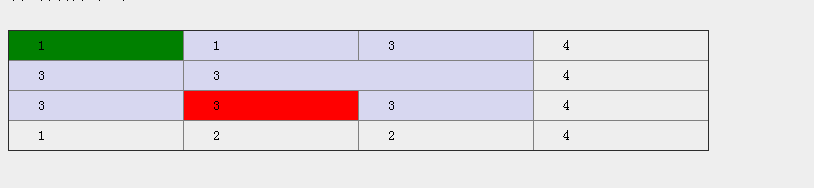
上圖紅色為終止點,綠色為起始點。
1.演算法
關鍵點1:合併單元格是通過rowspan,colspan來實現,意味一個單元格代替多個單元格,演算法中計算出的單元格位置需要與在視圖中看到的一致,所以和在左上角單元格(在邊界值組成的矩形中)在同一行的單元格刪除,不再同一行的隱藏。
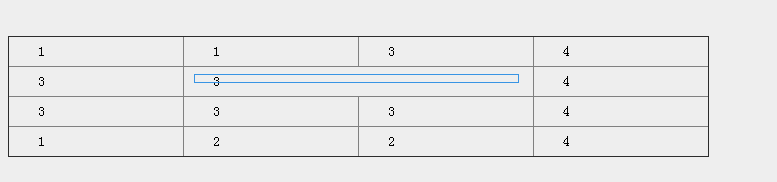
我們用left、top、right、bottom四個屬性來表示一個單元格的位置,上圖中被藍矩形標記的單元格位置為,left:1、top:1、right:3、bottom:2,上述做法主要為了確保left的獲取。
第一步:分別計算A、B兩個單元格的left、top、bottom、right,取得四個方向的最值來初步畫出一個矩形。關鍵代碼如下
getLeft($tr,$td){ let $tds = $tr.find("td"); let count = 0; for(let i=0;i<$tds.length;i++) { let $td_temp = $tds.eq(i); if($td_temp[0] == $td[0]) { return count; } let colspan = +$td_temp.attr("colspan") || 1; count += colspan; } }
得到單元格在所屬行的left屬性,right根據left屬性加1或colspan屬性值,top等同於所屬行的位置,bottom根據top屬性加上1或rowspan屬性值。
關鍵點2:當被合併的單元格中有已合併單元格的時候,可能出現某個單元格的四個屬性超出已劃定矩形的情況,一個邊界的變化又會影響到其他的邊界。所以需要迴圈確認最終矩形,直到無單元格位置溢出。
如下例:
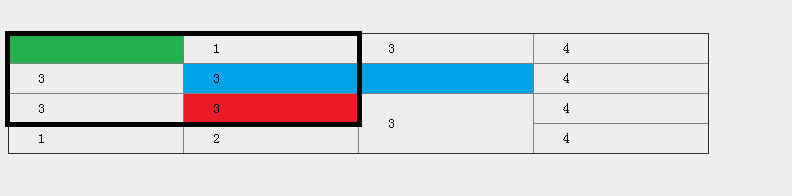
當選擇綠色矩形標記的單元格為起始點,紅色標記的單元格為終止點,黑色邊框是第一步組成的矩形,但藍色標記單元格的右邊界溢出,當調整矩形如下時
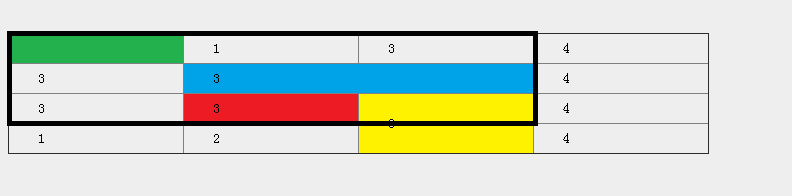
黃色標記的單元格bottom屬性溢出,最終為:

推算左邊界的值“
get_tdPosLeft($tr,pos){ let $tds = $tr.find("td"); let count = 0; let colspan = 0; for(let i=0;i<$tds.length;i++) { let $td_temp = $tds.eq(i); if(count == pos){ return count; } else if(count > pos){ return count - colspan; } colspan = +$td_temp.attr("colspan") || 1; count += colspan; } }
//pos的的值等於劃定的左邊界值,如果單元格的left屬性等於pos屬性,說明單元格left屬性沒有溢出,如果大於pos,則左邊界往左減1或者減去它的colspan屬性值
推算右邊界的值:
get_tdPosRight($tr,pos){ let $tds = $tr.find("td"); let count = 0; for(let i=0;i<$tds.length;i++) { let $td_temp = $tds.eq(i); let colspan = +$td_temp.attr("colspan") || 1; count += colspan; if(count == pos){ return count; } else if(count > pos){ return count; } } }
//
//pos的值等於劃定的右邊界值,如果單元格的right屬性等於pos屬性,說明單元格right屬性沒有溢出,如果大於pos,則右邊界溢出,返回單元格右邊界的值。
推算上邊界:
hasRowCollposed_top($tr,left,right){ let $tds = $tr.find("td"); let count = 0; for(let i=0;i<$tds.length;i++){ let $td = $tds.eq(i); if($td.hasClass("hidden_rwospan")){ if(count >= left && count < right){ return true; } else{ break; } } count += +$td.attr("colspan") || 1; } return false; }
//這裡的left、right等於以推算過後的左邊界值和右邊界值,如果在left和right之間有td元素含有
//hidden_rwospan類(因合併單元格而添加到元素上),說明上邊界溢出,返回true
.hidden_rwospan{
display:none;
}
如下圖:
第二行和第三行的html結構如下:
<tr> <td><span class="tab"> </span>3</td> <td rowspan="2"><span class="tab"> </span>3</td> <td><span class="tab"> </span>3</td> <td><span class="tab"> </span>4</td> </tr> <tr> <td ><span class="tab"> </span>3</td> <td class="hidden_rwospan"><span class="tab"> </span>3</td> <td><span class="tab"> </span>3</td> <td><span class="tab"> </span>4</td> </tr>
推算下邊界:下邊界有一個特殊情況,當發現在左右邊界記憶體在擁有hidden_rwospan類的單元格時,需要判定是否存在穿透的情況,如下圖
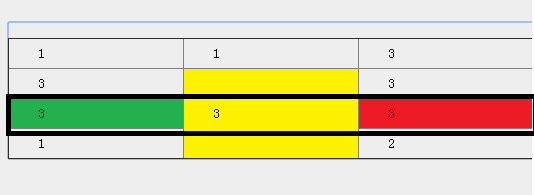
黃色標記的單元格穿透了最初劃定的邊界。hasRowCollposed_bottom($tr,left,right){
let $tds = $tr.find("td"); let count = 0; for(let i=0;i<$tds.length;i++){ let $td = $tds.eq(i); if(!$td.hasClass("hidden_rwospan")){ if(count >= left && count < right){ let rowspan = +$td.attr("rowspan") || 0; if(rowspan > 1){ return true; } } else if(count>=right){ break; } } else{ // 因為rowspan而隱藏的單元格 if(count >= left && count < right){ //如果隱藏 可能發生上面單元格的rowspan穿透了當前單元格 let right_pos = count + (+$td.attr("colspan") || 1); if (this.isCrossRow_collposed($td,$tr.next(),count,right_pos,left,right)) { return true; } } else if(count>=right){ break; } } count += +$td.attr("colspan") || 1; } return false; }
//沒被隱藏的單元格如果在範圍內有單元格擁有rowspan屬性且值大於1,則下邊界往下推,在範圍內擁有hidden_rwospan的元素,則需要判定是否發生穿透
判定是否發生穿透:
isCrossRow_collposed($td_compare,$tr_next,left_pos,right_pos,left,right){ //如果在左右邊界內有單元格擁有hidden_rwospan類,且left屬性和right屬性和left_pos、right_pos相同,則bottom需要往下推 //left_pos 對比單元格左邊的位置,right_pos 右邊的位置,left 組成矩形的左邊界,right 組成矩形右邊界 let $tds = $tr_next.find("td"); let count = 0; for(let i=0;i<$tds.length;i++){ let $td = $tds.eq(i); if($td.hasClass("hidden_rwospan")){ if(count >= left && count < right){ if(count == left_pos ){ let colspan = left_pos + ( +$td.attr("colspan") || 1); if(colspan == right_pos){ return true; } } else if(count > left_pos){ break; } } } if(count>=right){ break; } count += +$td.attr("colspan") || 1; } return false; }
核心代碼(Esl class語法):
getArra_collposed($td_start,$td_end){ //畫出最初矩形 let left = this.getFarLeft($td_start,$td_end);//得到最靠左單元格的left屬性值 let top = this.getFarTop($td_start,$td_end); let right = this.getFarRight($td_start,$td_end); let bottom = this.getFarBottom($td_start,$td_end); let $trs = this.$ele_current.find("tr"), $tr_top = $trs.eq(top), $tr_bottom = $trs.eq(bottom-1); while(true){ let left_temp = left, top_temp = top, right_temp = right, bottom_temp = bottom; for(let i=top;i<bottom;i++){ let $tr = $trs.eq(i); let pos = this.get_tdPosLeft($tr,left); if(left_temp > pos){ left_temp = pos; } } for(let i=top;i<bottom;i++){//推算右邊界 let $tr = $trs.eq(i); let pos = this.get_tdPosRight($tr,right); if(right_temp < pos){ right_temp = pos; } } if(this.hasRowCollposed_top($tr_top,left_temp,right_temp)){//推算上邊界 top_temp--; } if(this.hasRowCollposed_bottom($tr_bottom,left_temp,right_temp)){//推算下邊界 bottom_temp++; } if(left_temp == left && right_temp == right && top_temp == top && bottom_temp == bottom){ break; } else{
//有一個邊界值改變則重新推算 left = left_temp; right = right_temp; top = top_temp; bottom = bottom_temp; $tr_top = $trs.eq(top); $tr_bottom = $trs.eq(bottom-1); } } return {left,right,top,bottom}; }
得到四個邊界值就可以得到其內的單元格,以及rowspan屬性值大小和colspan屬性值大小,最後按照開頭說的,選取最終劃定矩型左上角的單元格進行合併即可,同行的刪除,不同行的隱藏。
測試的時候重現上述所說的狀態,保證所寫代碼邏輯都走一遍。