題目鏈接 Problem Description Suppose that you are an admiral of a famous naval troop. Our naval forces have got 21 battleships. There are 6 types of battl ...
Problem Description Suppose that you are an admiral of a famous naval troop. Our naval forces have got 21 battleships. There are 6 types of battleships.
First, we have got one flagship in which the admiral must be and it is denoted by number 0. Others are denoted by number from 1 to 5, each of them has 2, 3, 4, 5, 6 ships of its kind. So, we have got 21 battleships in total and we must take a giant battle against the enemy. Hence, the correct strategy of how to arrange each type of battleships is very important to us.
The shape of the battlefield is like the picture that is shown below.
To simplify the problem, we consider all battleships have the same rectangular shape.
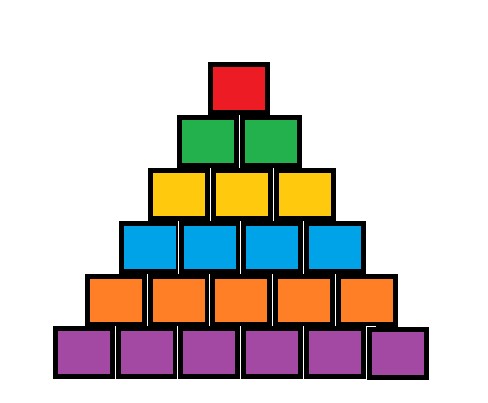
Fortunately, we have already known the optimal state of battleships.
As you can see, the battlefield consists of 6 rows. And we have 6 types of battleship, so the optimal state is that all the battleships denoted by number i are located at the i-th row. Hence, each type of battleship corresponds to different color.
You are given the initial state of battlefield as input. You can change the state of battlefield by changing the position of flagship with adjacent battleship.
Two battleships are considered adjacent if and only if they are not in the same row and share parts of their edges. For example, if we denote the cell which is at i-th row and j-th position from the left as (i,j), then the cell (2,1) is adjacent to the cells (1,0), (1,1), (3,1), (3,2).
Your task is to change the position of the battleships minimum times so as to reach the optimal state.
Note: All the coordinates are 0-base indexed.
Input The first line of input contains an integer T (1 <= T <= 10), the number of test cases.
Each test case consists of 6 lines. The i-th line of each test case contains i integers, denoting the type of battleships at i-th row of battlefield, from left to right.
Output For each test case, if you can’t reach the goal in no more than 20 moves, you must output “too difficult” in one line. Otherwise, you must output the answer in one line.
Sample Input 1 1 2 0 2 1 2 3 3 3 3 4 4 4 4 4 5 5 5 5 5 5
Sample Output 3 題意:有21個數由1個0、2個1、3個2、4個3、5個4和6個5組成,這21個數構成一個三角形,與楊輝三角一樣第一行1個數,第2行2個數……第6行6個數,現在要把這21個數歸位按順序擺好,0 在第一行,1在第二行……5在第六行,每次操作為0與它相鄰的數可以進行交換,同行之間不能進行交換,求最少經過多少步將所有數歸位,如果20步還我完成不了則輸出“too difficult”。 思路:搜索,但是直接搜20步會超時,所以可以從兩端各搜10步,這樣就降低了複雜度,另外可以用hash來保存狀態。 代碼如下:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <queue> #include <map> using namespace std; typedef long long LL; int dx[4]={1,1,-1,-1}; int dy[4]={0,1,-1,0}; struct Node{ LL p[6][6]; int r,c; int flag; int dept; }; queue<Node>Q; map<LL,int>M[2]; LL cal(Node a) { LL ans=0; for(int i=0;i<6;i++) { for(int j=0;j<=i;j++) { ans=ans*6+a.p[i][j]; } } return ans; } int bfs(Node &s,Node &e) { while(!Q.empty()) Q.pop(); M[0].clear(); M[1].clear(); M[0][cal(s)]=0; M[1][cal(e)]=0; Q.push(s); Q.push(e); while(!Q.empty()) { Node x=Q.front(); Q.pop(); LL sta=cal(x); if(M[!x.flag].count(sta)) { int num=M[!x.flag][sta]+x.dept; if(num<=20) return num; else continue; } if(x.dept>=10) continue; for(int i=0;i<4;i++) { Node y=x; y.dept++; y.r+=dx[i]; y.c+=dy[i]; if(y.r<0 || y.r>=6 || y.c<0 || y.c>y.r) continue; swap(y.p[x.r][x.c],y.p[y.r][y.c]); if(M[y.flag].count(cal(y))==0) M[y.flag][cal(y)]=y.dept; Q.push(y); } } return -1; } int main() { int T; cin>>T; Node s,e; while(T--) { for(int i=0;i<6;i++) { for(int j=0;j<=i;j++) { scanf("%lld",&s.p[i][j]); if(s.p[i][j]==0) s.r=i, s.c=j; e.p[i][j]=i; } } s.flag=0; s.dept=0; e.r=0; e.c=0; e.flag=1; e.dept=0; int ans=bfs(s,e); if(ans>=0&&ans<=20) printf("%d\n",ans); else puts("too difficult"); } return 0; } /** 1 2 1 2 0 2 3 3 3 3 4 4 4 4 4 5 5 5 5 5 5 0 1 1 2 2 2 3 3 3 3 4 4 4 4 4 5 5 5 5 5 5 */



