本文是在閱讀Aditya Bhargava先生演算法圖解一書所做的總結，文中部分代碼引用了原文的代碼，在此感謝Aditya Bhargava先生所作出的這麼簡單的事例，對基礎演算法感興趣的朋友可以閱讀原文。由於本人也是編程初學者，所以本書比較淺顯易懂，所介紹的演算法配上插圖也十分易懂，這裡只是介紹幾種最基礎的演算法由淺入深以幫助理順一些簡單的思維邏輯。

演算法簡介

　　演算法是一組完成任務的指令。任何代碼片段都可視為演算法，我們這裡討論的演算法要麼速度快，要麼能解決有趣的問題，要麼兼而有之。

二分查找

　　二分查找是一種演算法，其輸入是一個有序的元素列表，如果要 查找的元素包含在列表中，二分查找返回其位置；否則返回Null。

　　二分法很好理解，如果讓你猜出100以內指定的某個值的話，怎樣可以做到用最少的次數尋找到。可能有人覺得可能一次就可以找到，但是最糟可能要猜100次哦。

　　這種問題使用二分法就很簡便了，每次取中間值以縮小查找範圍，這樣7步以內必定可以找到答案。

　　如果這個問題擴大到4億的話，無疑二分法可要優秀的多。一般而言，對於包含n個元素的列表，用二分查找最多需要log2n步，而簡單查找最多需要n步。

　　二分法的有點事查找速度快，但是僅當列表是有序的時候，二分查找才管用。

　　對於這個猜數字的游戲使用二分法思想完成的代碼如下：

#二分法
def two(lists,item):
    low=0
    high=len(lists)-1
    while low<= high:
        mid=(low+high)//2
        guess=lists[mid]
        if guess==item:
            return  "guess is %s"%guess
        elif guess > item:
            high=mid-1
        else:
            low=mid+1
    return None
lists=[1,2,4,6,8]
print(two(lists,8))
print(two(lists,3))
運行結果：
guess is 8
None

大O表示法

　　大O表示法是一種特殊的表示法，指出了演算法的速度有多快。由於不同演算法運行時間的增速不同，所以使用大O表示法來看時間增速更為科學直觀。

　　例如假設列表包含n個元素。簡單查找需要檢查每個元素，因此需要執行n次操作。使用大O表示法，這個運行時間為O(n)。之所以稱為大O表示法，是因為操作數前有個大O。。。這是真的。

　　簡單查找的運行時間總是為O(n)。在電話簿查找Adit時，一次就找到了，這是最佳的情形，即O（1），但大O表示法說的是最糟的情形。因此，你可以說，在最糟情況下，必須查看電話簿中的每個條目，對應的運行時間為O(n)。

　　一些常見的大O運行時間

　　 O(log n)，也叫對數時間，這樣的演算法包括二分查找。

　　 O(n)，也叫線性時間，這樣的演算法包括簡單查找。

　　 O(n * log n)，這樣的演算法包括快速排序。

　　 O(n2 )，這樣的演算法包括選擇排序。

　　 O(n!)，這樣的演算法包括接下來將介紹的旅行商問題的解決方案。

　　使用這幾種演算法繪製一個16格的網格需要的時間如下：

　　速度由快到慢，當然只是針對這個問題而言。

　　 演算法的速度指的並非時間，而是操作數的增速。

　　 談論演算法的速度時，我們說的是隨著輸入的增加，其運行時間將以什麼樣的速度增加。

　　 演算法的運行時間用大O表示法表示。

　　 O(log n)比O(n)快，當需要搜索的元素越多時，前者比後者快得越多。

　　旅行商問題

　　這著實困擾著很多人，一位旅行商要去往5個城市，如何確保旅程最短，5個城市有120種不同的排列方式。涉及n個城市時，需要執行n!（n的階乘）次操作才能計算出結果。因此運行時間為O(n!)，即階乘時間。

選擇排序

　　很多演算法僅在數據經過排序後才管用。當然很多語言都內置了排序演算法，因此你基本 上不用從頭開始編寫自己的版本。

　　數組與鏈表

　　需要將數據存儲到記憶體時，你請求電腦提供存儲空間，電腦給你一個存儲地址。需要存儲多項數據時，有兩種基本方式——數組和鏈表。

　　數組中的記憶體必須是相連的，這意味著增加元素的時候如果緊跟著的那個記憶體被占用了，那就只能重新尋找可容納的連續地址，如果沒有這麼長的連續地址結果還存不了，所以電腦在存數組時還預留了空間，你只要三個記憶體，但是我給你十個。即使如此額外請求的位置可能根本用不上，這將浪費記憶體，你沒有使用，別人也用不了。而且待辦事項超過10個後，你還得轉移。

　　鏈表中的元素可存儲在記憶體的任何地方。鏈表的每個元素都存儲了下一個元素的地址，從而使一系列隨機的記憶體地址串在一起。在鏈表中添加元素很容易：只需將其放入記憶體，並將其地址存儲到前一個元素中，刪除也是如此。但是鏈表在讀取上要明顯弱於數組，要讀取最後一個記憶體的內容必須要按順序依次讀到最後一個位置為止，數組可以隨意讀取中間任意位置的內容（因為知道第一塊記憶體地址可以推出第幾塊地址的位置，他們是連續的）。

數組與鏈表的操作運行時間

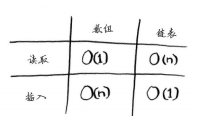
 　　數組和鏈表哪個用得更多呢？顯然要看情況。但數組用得很多，因為它支持隨機訪問，很多情況都要求能夠隨機訪問，而不是順序訪問。

　　選擇排序

　　比如網易雲音樂要根據你聽歌的次數排序你喜歡的音樂，可以每次都迴圈列表，每次取出最高次數的音樂放入新列表，直到原列表為空時結束。則總時間為1/2O（n**2），大O法省略常數，所以也就是時間為O（n**2）。

　　選擇排序的代碼：

#O(n**2)
def low(arr):
    lowest=0
    arrlow=arr[0]
    for i1 in range(1,len(arr)):
        if arr[i1] < arrlow:
            arrlow=arr[i1]
            lowest=i1
    return lowest

def sor(arr):
    new_arr=[]
    for i in range(len(arr)):
        smaller=low(arr)
        new_arr.append(arr.pop(smaller))
    return new_arr
print(sor([3,2,9,6,4]))
運行結果：
[2, 3, 4, 6, 9]

　　註：同一數組的元素類型都必須相同。

遞歸

　　遞歸指的是調用自己的函數，遞歸只是讓解決方案更清晰，並 沒有性能上的優勢。實際上，在有些情況下，使用迴圈的性能更好。Leigh Caldwell在Stack Overflow上說的一句話：“如果使用迴圈，程式的性能可能更高；如果使用遞歸，程式可能 更容易理解。如何選擇要看什麼對你來說更重要。”

　　基線條件和遞歸條件

　　編寫遞歸函數時，必須告訴它何時停止遞歸。正因為如此，每個遞歸函數都有兩部分：基線 條件（base case）和遞歸條件（recursive case）。遞歸條件指的是函數調用自己，而基線條件則指的是函數不再調用自己的條件，從而避免形成無限迴圈。

#遞歸求階乘
def fac(num):
    if num==1:
        return 1
    else:
        return num*fac(num-1)
print(fac(5))
運行結果：
120

#遞歸疊加
def ad(lis):
    if lis==[]:
        return 0
    else:
        return lis.pop(0)+ad(lis)
print(ad([1,2,3]))
運行結果：
6

#遞歸計數
def num(lis):
    n=0
    if lis ==[]:
        return n
    else:
        lis.pop()
        n+=1
        n+=num(lis)
        return n
print(num([1,2,3,4,5]))
運行結果：
5

#遞歸求最大值
def ma(lis):
    m=lis[0]
    if len(lis) ==1:
        return m
    else:
        tmp=ma(lis[1:])
        if tmp > m:
            m=tmp
        return m
print(ma([7,3,10,4,6]))
運行結果：
10

　　堆與棧

　　這個概念大家一定都比較清楚，這是經常使用的兩種編程概念，堆也叫隊列，指的是先進先出，棧則相反指的是後進先出，可以想一想python中的嵌套函數的調用，裡層的函數是後定義的但是卻先執行完，執行完有返回外層函數，這個調用函數就是調用棧的概念。規範的說他們只有壓入和彈出兩種狀態。

　　使用棧也存在一些缺點，存儲詳盡的信息可能占用大量的記憶體。每個函數調 用都要占用一定的記憶體，如果棧很高，就意味著電腦存儲了大量函數調用的信息。那麼你只能使用迴圈完成或者尾遞歸（這個高級方法我還不會）。

快速排序

　　分而治之

　　假設要將一塊土地均勻分成方塊，並且確保方塊最大。可以使用D&C策略。D&C演算法是遞歸的。

　　使用D&C解決問題的過程包括兩個步驟：

　　 (1) 找出基線條件，這種條件必須儘可能簡單。

　　(2) 不斷將問題分解（或者說縮小規模），直到符合基線條件。

　　根據D&C的定義，每次遞歸調用都必須 縮小問題的規模。這個問題的基線條件就是一條邊的長度是另一條邊的整數倍。以短邊為基準，在長邊取短邊*n的最大取值，剩下的部分依次按上述操作，直到最後長邊為短邊的整數倍位置短邊**2就是最大方形了。

　　D&C的工作原理：

　　(1) 找出簡單的基線條件；

　　(2) 確定如何縮小問題的規模，使其符合基線條件。

　　D&C並非可用於解決問題的演算法，而是一種解決問題的思路。

　　快速排序

　　快速排序使用了D&C。對排序演算法來說，基線條件為數組為空或只包含一個元素。

　　首先，從數組中選擇一個元素，這個元素被稱為基準值；

　　接下來，找出比基準值小的元素以及比基準值大的元素。

　　再對這兩個子數組進行快速排序，直到滿足基線條件。

　　註：歸納證明是一種證明演算法行之有效的方式，它分兩步：基線 條件和歸納條件。

#快速排序
def quicksrt(arr):
    if len(arr)<2:
        return arr
    else:
        pio=arr[0]
        less=[i for i in arr[1:] if i<pio]
        than=[i for i in arr[1:] if i>=pio]
        return quicksrt(less)+[pio]+quicksrt(than)
print(quicksrt([4,5,7,2,3,9,4,0]))
運行結果：
[0, 2, 3, 4, 4, 5, 7, 9]

　　快速排序的最糟情況運行時間為O（n**2），與選擇排序一樣慢，但是他的平均排序時間為O（n*log n）。而合併排序總是O（n*log n）。但是這不是絕對的，合併排序的常量總是大於快速排序，所以一般情況下認為快速排序更快。

　　平均情況與最糟情況

　　假設要為從小到大的多個數排序，最糟情況就是每次都選第一個值作為基準值，這樣每次操作時間都是O（n），共操作O（n）次，該演算法的運行時間為O(n) * O(n) = O(n**2 )。而最佳情況每次都能選擇最中間的數來排，就好像二分法一樣層數為O(log n)（用技術術語說，調用棧的高度為O(log n)），而每層需要的時間為O(n)。因此整個演算法需要的時間為O(n) * O(log n) = O(n log n)。

散列表

　　散列函數

　　散列函數“將輸入映射到數字”。這個用python字典比較好理解，每次給定key都得到的是同一個數字，每個key都對應一個value。

　　 散列函數總是將同樣的輸入映射到相同的索引。

　　 散列函數將不同的輸入映射到不同的索引。

　　 散列函數知道數組有多大，只返回有效的索引。

　　說到字典你可能根本不需要自己去實現散列表，任一優秀的語言都提供了散列表實現。Python提供的散列表實現就是字典，你可使用函數dict來創建散列表。

　　這樣散列表的概念就非常好理解了，散列表通常用於查找，在網站投票中還可以過濾掉已經投過票的人，也就是去重，還有就是對於一些經常訪問的網站進行緩存也使用了散列表。緩存是一種常用的加速方式，所有大型網站都使用緩存，而緩存的數據則存儲在散列表中。

　　衝突

　　間接描述了散列表的性能，衝突就是：給兩 個鍵分配的位置相同。處理衝突的方式 很多，最簡單的辦法如下：如果兩個鍵映射到了同一個位置，就在這個位置存儲一個鏈表。如果一個散列表所有的值都放在第一個記憶體中呢，那和一個鏈表又有什麼區別呢？最理想的情況是， 散列函數將鍵均勻地映射到散列表的不同位置。如果散列表存儲的鏈表很長，散列表的速度將急劇下降。

　　性能

　　在平均情況下，散列表執行各種操作的時間都為O(1)。我們來將 散列表同數組和鏈表比較一下。

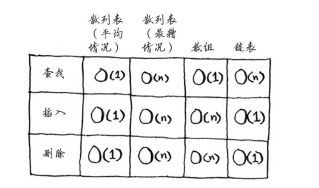
　　填裝因數

　　用來描述性能的參數，值為散列表的元素數/位置總數。填裝因數大於1時意味元素數大於位置數，這個時候可能就是要考慮調整散列表長度了。調整散列表長度的工作需要很長時間！你說得沒錯，調整長度的開銷很大，因 此你不會希望頻繁地這樣做。但平均而言，即便考慮到調整長度所需的時間，散列表操作所需的時間也為O(1)。

廣度優先搜索

　　如果你要從A點去往B點，這種問題被稱為最短路徑問題需要兩個步驟。

　　 (1) 使用圖來建立問題模型。

　　(2) 使用廣度優先搜索解決問題。

　　圖是由節點和邊組成的，圖用於模擬不同的東西是如何相連的。

　　廣度優先搜索是一種用於圖的查找演算法，可幫助回答兩類問題。

　　 第一類問題：從節點A出發，有前往節點B的路徑嗎？

　　 第二類問題：從節點A出發，前往節點B的哪條路徑最短？

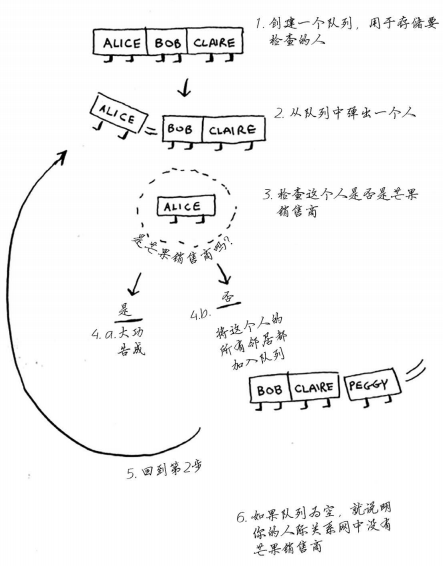
　　廣度優先的工作原理圖

　　要看你的認識的人中有沒有芒果銷售員，從你的朋友開始查每查一個朋友就把他的朋友加入你的查找列表隊列的末尾，直到查完為止或者找到的第一個芒果銷售員。在此過程中對於已經查過的人單獨拿出來，因為重覆查無意義甚至導致無限迴圈。

　　註： 有向圖中的邊為箭頭，箭頭的方向指定了關係的方向，例如，rama→adit表示rama欠adit錢。 無向圖中的邊不帶箭頭，其中的關係是雙向的，例如，ross - rachel表示“ross與rachel約 會，而rachel也與ross約會”。

狄克斯特拉演算法

　　還是解決最短路徑的演算法，不過他解決的是加權圖的最短路徑。也就是說在狄克斯特拉演算法中，你給每段都分配了一個數字或權重，因此狄克斯特拉演算法找出 的是總權重最小的路徑。

　　狄克斯特拉演算法包含4個步驟。

　　(1) 找出“最便宜”的節點，即可在最短時間內到達的節點。

　　(2) 更新該節點的鄰居的開銷。

　　(3) 重覆這個過程，直到對圖中的每個節點都這樣做了。

　　(4) 計算最終路徑。

　　要計算非加權圖中的最短路徑，可使用廣度優先搜索。要計算加權圖中的最短路徑，可使用狄克斯特拉演算法。

　　要註意的是狄克斯特拉演算法只適用於無環圖，並且狄克斯特拉演算法無法計算負權的邊。帶負權的邊要使用貝爾曼福德演算法計算（這個我也不會）。

　　下麵代碼就實現了狄克斯特拉演算法計算出最短路徑的代碼。

# 迪克斯塔拉演算法求最短路徑
graph = {}#先描述距離
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

graph["a"] = {}
graph["a"]["fin"] = 1

graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5

graph["fin"] = {}

# 權重表
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

processed = []#已經算過的列表

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")#終點無限大
    lowest_cost_node = None
    # 遍歷每一個節點
    for node in costs:
        cost = costs[node]
        # 判斷大小並且之前未計算過
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost#如果有更小距離則更新
            lowest_cost_node = node
    return lowest_cost_node

# 未處理的成本最低的節點.
node = find_lowest_cost_node(costs)
# 處理完所有節點時迴圈結束
while node is not None:
    cost = costs[node]
    # 通過節點的所有鄰居
    neighbors = graph[node]
    for n in neighbors.keys():
        new_cost = cost + neighbors[n]#從此節點計算到下一節點的開銷
        # 如果是去這個鄰居通過這個節點更便宜
        if costs[n] > new_cost:
            # 更新此節點最小值
            costs[n] = new_cost
            # 節點成為鄰居最近的下一節點
            parents[n] = node
    #節點標記為已處理
    processed.append(node)
    #發現下一個節點與環
    node = find_lowest_cost_node(costs)

print("Cost from the start to each node:")
print(costs)
運行結果：
Cost from the start to each node:
{'a': 5, 'fin': 6, 'b': 2}

貪婪演算法

　　貪婪演算法很簡單：每步都採取最優的做法，最終得到的就是全局最優解。貪婪演算法並非在任何情況下都行之有效，但它易於實現。

　　用一個簡單的例子來解釋一下。比如有下麵一張課程表，你學要儘可能多的在一間教室里上最多的課。

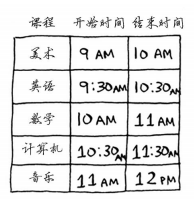
　　(1) 選出結束最早的課，它就是要在這間教室上的第一堂課。

　　(2) 接下來，必須選擇第一堂課結束後才開始的課。同樣，你選擇結束最早的課，這將是要在這間教室上的第二堂課。

　　(3)重覆第二步。

　　這就是貪婪演算法。雖然貪婪演算法是萬能的但是他往往不是最優的，但是對於一些沒有更好的解決方法，貪婪演算法往往是最有效的。

　　集合覆蓋問題

　　假設你辦了一個電視節目你想在全國上映，但是每個電視臺覆蓋的範圍都不一樣，還可能有重覆覆蓋的區域。

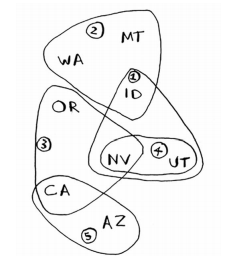
　　(1) 列出每個可能的廣播台集合，這被稱為冪集（power set）。可能的子集有2n個。

　　(2) 在這些集合中，選出覆蓋全美50個州的最小集合。問題是計算每個可能的廣播檯子集需要很長時間。由於可能的集合有2**n個，因此運行時間為 O(2**n )。

　　貪婪演算法可化解危機！使用下麵的貪婪演算法可得到非常接近的解。

　　(1) 選出這樣一個廣播台，即它覆蓋了最多的未覆蓋州。即便這個廣播台覆蓋了一些已覆蓋的州，也沒有關係。

　　(2) 重覆第一步，直到覆蓋了所有的州。

　　這是一種近似演算法（approximation algorithm）。在獲得精確解需要的時間太長時，可使用近似演算法。

　　判斷近似演算法優劣的標準如下：

　　 速度有多快；

　　 得到的近似解與最優解的接近程度。

　　這個問題的演算法代碼：

states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])

stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set()

while states_needed:
  best_station = None
  states_covered = set()
  for station, states in stations.items():
    covered = states_needed & states
    if len(covered) > len(states_covered):
      best_station = station
      states_covered = covered

  states_needed -= states_covered
  final_stations.add(best_station)

print(final_stations)
運行結果；
{'kone', 'ktwo', 'kthree', 'kfive'}

　　貪婪演算法還可以求出旅行商問題的簡單答案。

　　NP完全問題的簡單定義是，以難解著稱的問題，如旅行商問題和集合覆蓋問題。NP演算法本身不難，但是界定哪些問題應該使用NP演算法求解更優卻是個難點。要判斷問題是不是NP完全問題很難，易於解決的問題和NP完全問題的差別通常很小。

　　如何判斷問題是不是NP完全問題：

　　 元素較少時演算法的運行速度非常快，但隨著元素數量的增加，速度會變得非常慢。

　　 涉及“所有組合”的問題通常是NP完全問題。

　　 不能將問題分成小問題，必須考慮各種可能的情況。這可能是NP完全問題。

　　 如果問題涉及序列（如旅行商問題中的城市序列）且難以解決，它可能就是NP完全問題。

　　 如果問題涉及集合（如廣播台集合）且難以解決，它可能就是NP完全問題。

　　 如果問題可轉換為集合覆蓋問題或旅行商問題，那它肯定是NP完全問題。

動態規劃

　　背包問題

　　一個小偷，背包容納量為4，商店有三件商品可以偷，音響3000塊重量4，電腦2000塊重量3，吉他1500塊重量1。

　　嘗試一次次的試，時間為O（2**n），這種方法肯定可以使用NP演算法啦，但是不是最優解。

　　動態規劃先解決子問題，再逐步解決大問題。

　　每個動態規划算法都從一個網格開始，背包問題的網格如下。

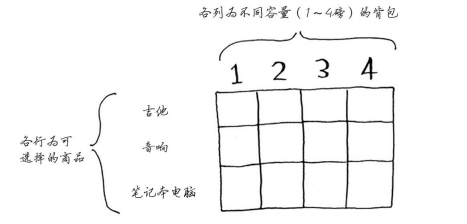
　　第一行是吉他行，你只能選擇拿不拿吉他，只能拿其他肯定會拿偷啊，這樣利益最大化。

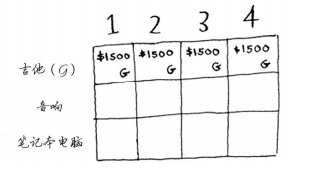
　　第二行是音箱行，你可以選擇吉他或音箱。

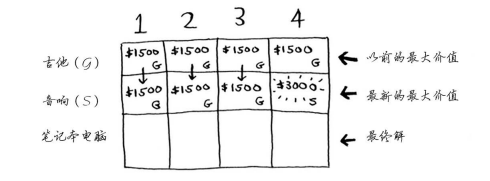
　　第三行電腦行，三種都可以選擇。

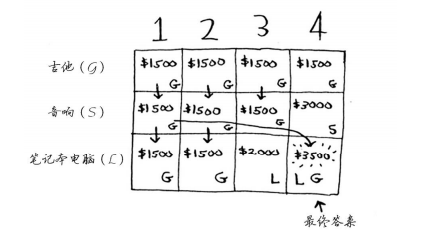
　　這裡行排列的順序變化了對結果沒什麼影響。並且最優解可能背包還沒裝滿。

　　但僅當 每個子問題都是離散的，即不依賴於其他子問題時，動態規劃才管用。

K最近鄰演算法

　　抽取事物特征併在坐標軸上給出橫縱坐標打分，這等於抽象出空間中的點，然後使用畢達哥拉斯公式計算與其他點的距離來判斷與哪些點更為相似。

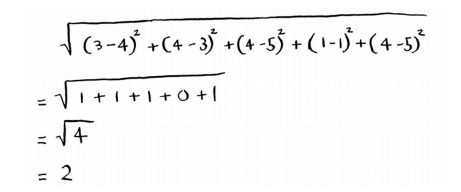
　　Priyanka和Morpheus的距離為24，所以可得出Priyanka的喜好更接近於Justin而不是Morpheus的結論。這樣就可以依據Justin的喜好給Priyanka推薦電影啦。

　　回歸

　　假設你不僅要向Priyanka推薦電影，還要預測她將給這部電影打多少分。為此，先找出與她最近的多個人，你求這些人打的分的平均值，結果為4.2。這就是回歸（regression）。

　　你將使用KNN來做兩項 基本工作——分類和回歸：

　　 分類就是編組；

　　 回歸就是預測結果（如一個數字）。

　　比起距離計算，我們平時工作中使用餘弦相似度來打分更為準確常用。

　　KNN演算法廣泛應用於機器學習領域。OCR指的是光學字元識別（optical character recognition），這意味著你可拍攝印刷頁面的照片，電腦將自動識別出其中的文字。

　　使用KNN。

　　(1) 瀏覽大量的數字圖像，將這些數字的特征提取出來。

　　(2) 遇到新圖像時，你提取該圖像的特征，再找出它最近的鄰居都是誰！

　　OCR演算法提取線段、點和曲線等特征。遇到新字元時，可從中提取同樣的特征。

　　這僅僅是編程演算法的一小部分，在後面還有很多高級的演算法等著我們，對於本文的一些代碼，如果不太懂他的運行過程可以使用debug一步一步推導出來，演算法是編程中極為核心的部分，你的代碼的優秀程度與你的思維有很大的關係，希望初學python編程也能很有好的思維方式來解決遇到的問題，因為讀這本書比較淺顯，閱讀也很快，所以可能存在著一些問題，希望各路大神批評指正