題目鏈接 Problem Description The center coordinate of the circle C is O, the coordinate of O is (0,0) , and the radius is r.P and Q are two points not out ...
Problem Description The center coordinate of the circle C is O, the coordinate of O is (0,0) , and the radius is r.
P and Q are two points not outside the circle, and PO = QO.
You need to find a point D on the circle, which makes PD+QD minimum.
Output minimum distance sum.
Input The first line of the input gives the number of test cases T; T test cases follow.
Each case begins with one line with r : the radius of the circle C.
Next two line each line contains two integers x , y denotes the coordinate of P and Q.
Limits
T≤500000
−100≤x,y≤100
1≤r≤100
Output For each case output one line denotes the answer.
The answer will be checked correct if its absolute or relative error doesn't exceed 10−6.
Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if |a−b|max(1,b)≤10−6.
Sample Input 4 4 4 0 0 4 4 0 3 3 0 4 0 2 2 0 4 0 1 1 0
Sample Output 5.6568543 5.6568543 5.8945030 6.7359174 題意:有一個圓,圓心在原點,輸入半徑 r ,圓內有兩個點P , Q 到圓心距離相同,現在求在圓上找一點M,使得PM+QM最小? 思路:
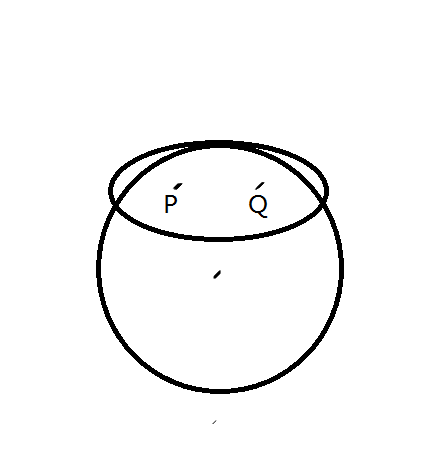
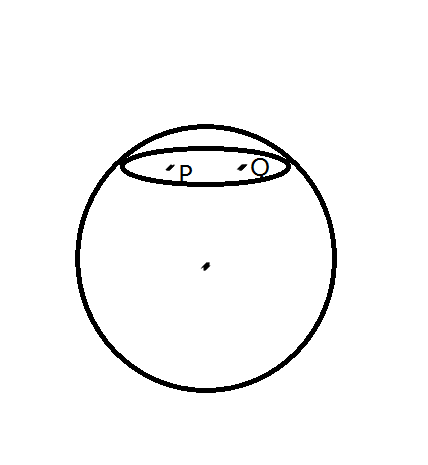
 對於圓內的兩個點 P 和 Q ,如果以其作為橢圓兩個焦點,由圖一可以看到:當橢圓頂點與圓相切時 , 圓與橢圓會有三個焦點,而橢圓上的點到P、Q的距離和是定值。那麼可以縮小橢圓,接下來會有四個交點,繼續縮小橢圓,得到圖二,橢圓與圓只有兩個交點,因為橢圓外的點到兩個焦點的距離和大於2a,而橢圓上的點到兩個焦點的距離和為2a,。在圖2中,除了兩個交點外,其餘圓上點均在橢圓外,所以這時的交點到P、Q兩點的距離和最小,等於2a。
如何找到這個相切的橢圓呢?二分解決。
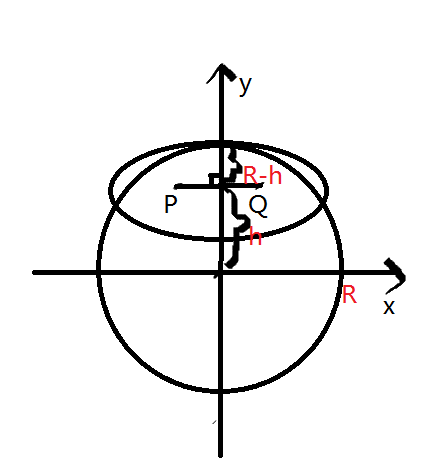
具體:由P、Q兩個焦點,我們可以確定c=PQ/2 , 現在如果再給出一個b值那麼就能確定這個橢圓了,而b值越大橢圓越大,b值越小橢圓越小,所以我們要找到如圖2所示,相切只有兩個焦點時的b值,那麼我們需要找的就是圓和橢圓相交時最小的b。我們可以求出圖3中所示的 h 和 R -h ,那麼橢圓的方程為:x^2/a^2 + (y-h)^2/b^2 = 1 ( 這個方程是PQ平行於X軸時的,但PQ不平行於X時也不影響,我們只是用它判斷是否與圓相交 ) 圓:x^2 + y^2 =R^R , 並且b>0(顯然),b<R-h ,所以在(0,R-h) 二分查找b。
代碼如下:
對於圓內的兩個點 P 和 Q ,如果以其作為橢圓兩個焦點,由圖一可以看到:當橢圓頂點與圓相切時 , 圓與橢圓會有三個焦點,而橢圓上的點到P、Q的距離和是定值。那麼可以縮小橢圓,接下來會有四個交點,繼續縮小橢圓,得到圖二,橢圓與圓只有兩個交點,因為橢圓外的點到兩個焦點的距離和大於2a,而橢圓上的點到兩個焦點的距離和為2a,。在圖2中,除了兩個交點外,其餘圓上點均在橢圓外,所以這時的交點到P、Q兩點的距離和最小,等於2a。
如何找到這個相切的橢圓呢?二分解決。
具體:由P、Q兩個焦點,我們可以確定c=PQ/2 , 現在如果再給出一個b值那麼就能確定這個橢圓了,而b值越大橢圓越大,b值越小橢圓越小,所以我們要找到如圖2所示,相切只有兩個焦點時的b值,那麼我們需要找的就是圓和橢圓相交時最小的b。我們可以求出圖3中所示的 h 和 R -h ,那麼橢圓的方程為:x^2/a^2 + (y-h)^2/b^2 = 1 ( 這個方程是PQ平行於X軸時的,但PQ不平行於X時也不影響,我們只是用它判斷是否與圓相交 ) 圓:x^2 + y^2 =R^R , 並且b>0(顯然),b<R-h ,所以在(0,R-h) 二分查找b。
代碼如下:
#include <iostream> #include <stdio.h> #include <math.h> #include <algorithm> using namespace std; const double eps = 1e-10; double dis(double x1,double y1,double x2,double y2 ) { return sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)); } namespace IO { const int MX = 4e7; //1e7占用記憶體11000kb char buf[MX]; int c, sz; void begin() { c = 0; sz = fread(buf, 1, MX, stdin); } inline bool read(int &t) { while(c < sz && buf[c] != '-' && (buf[c] < '0' || buf[c] > '9')) c++; if(c >= sz) return false; bool flag = 0; if(buf[c] == '-') flag = 1, c++; for(t = 0; c < sz && '0' <= buf[c] && buf[c] <= '9'; c++) t = t * 10 + buf[c] - '0'; if(flag) t = -t; return true; } } int main() { IO::begin(); int T; double R,x1,x2,y1,y2; double x3,y3; double A,B,C,dt,ans1,ans2; //cin>>T; IO::read(T); while(T--) { //scanf("%lf%lf%lf%lf%lf",&R,&x1,&y1,&x2,&y2); int xr, xx1, xx2, yy1, yy2; IO::read(xr); IO::read(xx1); IO::read(yy1); IO::read(xx2); IO::read(yy2); R = xr; x1 = xx1;y1 = yy1;x2 = xx2;y2 = yy2; double c=dis(x1,y1,x2,y2)*0.5; c=c*c; x3=(x1+x2)*0.5; y3=(y1+y2)*0.5; double h=dis(x3,y3,0.0,0.0); //cout<<h<<endl; double Rb=R-h; double Lb=0.0,b,a,mid; for(int i=0; i<30; i++) { mid=(Lb+Rb)*0.5; b = mid; b=b*b; a=c+b; A=a-b; B=2.0*a*h; C=b*R*R+a*h*h-a*b; dt=B*B-4.0*A*C; int flag=1; if(dt>=-eps) { ans1=(-B+sqrt(B*B-4.0*A*C))*0.5/A; ans2=(-B-sqrt(B*B-4.0*A*C))*0.5/A; ans1=ans1*ans1; ans2=ans2*ans2; if(R*R-ans1>=-eps||R*R-ans2>=-eps) flag=0; } if(flag==0) Rb=mid; else Lb=mid; } printf("%.10f\n",sqrt(a)*2.0); } return 0; }



