題目描述 牛牛最近迷上了一種叫鬥地主的撲克游戲。鬥地主是一種使用黑桃、紅心、梅花、方片的A到K加上大小王的共54張牌來進行的撲克牌游戲。在鬥地主中,牌的大小關係根據牌的數位表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色並不對牌的大小產生影響。每一局游戲中,一副手牌 ...
題目描述
牛牛最近迷上了一種叫鬥地主的撲克游戲。鬥地主是一種使用黑桃、紅心、梅花、方片的A到K加上大小王的共54張牌來進行的撲克牌游戲。在鬥地主中,牌的大小關係根據牌的數位表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色並不對牌的大小產生影響。每一局游戲中,一副手牌由n張牌組成。游戲者每次可以根據規定的牌型進行出牌,首先打光自己的手牌一方取得游戲的勝利。
現在,牛牛隻想知道,對於自己的若幹組手牌,分別最少需要多少次出牌可以將它們打光。請你幫他解決這個問題。
需要註意的是,本題中游戲者每次可以出手的牌型與一般的鬥地主相似而略有不同。
具體規則如下:
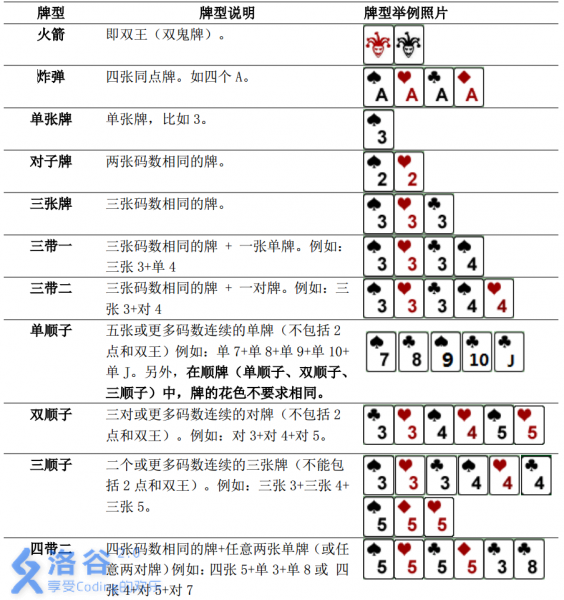
輸入輸出格式
輸入格式:第一行包含用空格隔開的2個正整數T和n,表示手牌的組數以及每組手牌的張數。
接下來T組數據,每組數據n行,每行一個非負整數對aibi表示一張牌,其中ai示牌的數位,bi表示牌的花色,中間用空格隔開。特別的,我們用1來表示數位A,11表示數位J,12表示數位Q,13表示數位K;黑桃、紅心、梅花、方片分別用1-4來表示;小王的表示方法為01,大王的表示方法為02。
輸出格式:共T行,每行一個整數,表示打光第i手牌的最少次數。
輸入輸出樣例
輸入樣例#1:1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1輸出樣例#1:
3輸入樣例#2:
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2輸出樣例#2:
6
說明
樣例1說明
共有1組手牌,包含8張牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通過打單順子(方片7,方片8,黑桃9,方片10,黑桃J),單張牌(黑桃5)以及對子牌(黑桃A以及方片A)在3次內打光。
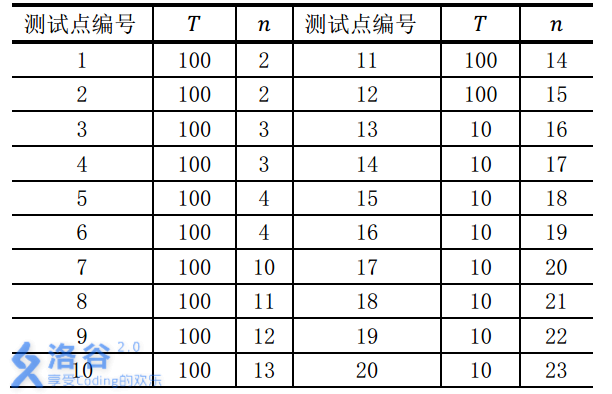
對於不同的測試點, 我們約定手牌組數T與張數n的規模如下:
數據保證:所有的手牌都是隨機生成的。
尼瑪廣搜323行85分,深搜壓行之後57行就A了,,,‘
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const int MAXN=23; 7 int read(int & n) 8 { 9 char c='-';int x=0; 10 while(c<'0'||c>'9')c=getchar(); 11 while(c>='0'&&c<='9') 12 { 13 x=x*10+(c-48); 14 c=getchar(); 15 } 16 n=x; 17 } 18 int T,n,p,hs; 19 int ans; 20 int card_num[MAXN];// 記錄每一種數位的出現次數 21 int happen[MAXN];// 記錄數量的出現次數 22 /*比如說3出現了兩次,A出現了兩次,那麼happen[2]==2*/ 23 int take_num[5]={0,5,3,2};// 鬥地主的規則,分別對應單順雙順三順 24 void dfs(int now)// now是指已經操作的次數 25 { 26 if(now>ans) 27 return ;// 剪枝 28 memset(happen,0,sizeof(happen)); 29 for(int i=0;i<=14;i++) 30 happen[card_num[i]]++; 31 int cs=0;// 本輪的操作次數 32 while(happen[4])// 四帶 33 { 34 cs++; 35 happen[4]--; 36 if(happen[2]>=2)//根據貪心的原理,能出兩張則不出一張 37 happen[2]-=2;// 能帶兩對對牌不帶一對對牌 38 else if(happen[1]>=2) 39 happen[1]-=2;//四張牌每次可以帶兩張單牌 40 } 41 while(happen[3]) 42 { 43 cs++; 44 happen[3]--; 45 if (happen[2]) 46 happen[2]--; 47 else if(happen[1]) 48 happen[1]--;//思路同上,三張牌進行帶牌的時候只能帶一張 49 } 50 if(card_num[0]&&card_num[1]&&happen[1]>=2) 51 cs--;//當大王和小王可以同時出的時候就當做對牌一起出 52 // 因為在後面一條語句中需要+happen[1],所以預設是大王小王當單牌出 53 // 那麼同時有大王小王就需要兩次操作,實際上一次操作就可以完成,相當於2-1=1 54 cs=cs+happen[1]+happen[2]; 55 // 剩下的對牌和單牌需要每組一次操作 56 ans=min(ans,cs+now);// 更新答案 57 for(int k=1;k<=3;k++)// k代表順子的類型,1:單順 2:雙順 3:三順 58 { 59 for(int i=3,j;i<=14;++i)// 枚舉每一張牌,因為2不能在順子中出現,所以無視 60 { 61 for(j=i;card_num[j]>=k&&j<=14;++j) 62 {//在可行的情況和區間內尋找順子 63 card_num[j]-=k;// 先減去,後面會加回來 64 if(j-i+1>=take_num[k])// 可以當順子出 65 dfs(now+1);// 就當順子出 66 } 67 while(j>i)// 遞歸的回溯 68 card_num[--j]+=k; 69 } 70 } 71 72 } 73 int main() 74 { 75 read(T);read(n); 76 while(T--) 77 { 78 memset(card_num,0,sizeof(card_num)); 79 ans=n; 80 for(int i=1;i<=n;i++) 81 { 82 read(p);read(hs); 83 if(p==0)card_num[hs-1]++; 84 // 把小王看做0,大王看做1.保證card_num數組沒有衝突 85 else if(p==1)card_num[14]++;// 把A看做14 86 else card_num[p]++; 87 } 88 89 dfs(0); 90 printf("%d\n",ans); 91 } 92 return 0; 93 }



