1807. [NOIP2014]尋找道路P2296 尋找道路

題目描述

在有向圖G 中，每條邊的長度均為1 ，現給定起點和終點，請你在圖中找一條從起點到終點的路徑，該路徑滿足以下條件：

1 ．路徑上的所有點的出邊所指向的點都直接或間接與終點連通。

2 ．在滿足條件1 的情況下使路徑最短。

註意：圖G 中可能存在重邊和自環，題目保證終點沒有出邊。

請你輸出符合條件的路徑的長度。

輸入輸出格式

輸入文件名為road .in。

第一行有兩個用一個空格隔開的整數n 和m ，表示圖有n 個點和m 條邊。

接下來的m 行每行2 個整數x 、y ，之間用一個空格隔開，表示有一條邊從點x 指向點y 。

最後一行有兩個用一個空格隔開的整數s 、t ，表示起點為s ，終點為t 。

輸出文件名為road .out 。

輸出只有一行，包含一個整數，表示滿足題目᧿述的最短路徑的長度。如果這樣的路徑不存在，輸出- 1 。

輸入輸出樣例

3 2  
1 2  
2 1  
1 3  

-1

6 6  
1 2  
1 3  
2 6  
2 5  
4 5  
3 4  
1 5  

3

說明

解釋1：

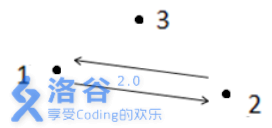
如上圖所示，箭頭表示有向道路，圓點表示城市。起點1 與終點3 不連通，所以滿足題

目᧿述的路徑不存在，故輸出- 1 。

解釋2：

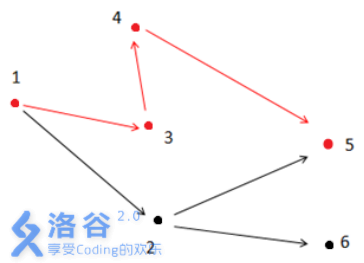
如上圖所示，滿足條件的路徑為1 - >3- >4- >5。註意點2 不能在答案路徑中，因為點2連了一條邊到點6 ，而點6 不與終點5 連通。

對於30%的數據，0<n≤10，0<m≤20；

對於60%的數據，0<n≤100，0<m≤2000；

對於100%的數據，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

這道題我們可以用逆向思維來想

如果一個點能到達終點，那麼終點也一定能到達這個點

這樣就簡單了

從終點跑一遍BFS，算出每一個點的訪問次數

然後把不能走的點刪去

最後spfa帶走

一個很有意思的能夠找出訪問次數而且不會死迴圈的方法

1 int to=edge[i].v;

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<queue>
  6 #define INF 0x7ffffff
  7 using namespace std;
  8 int read(int & n)
  9 {
 10     int flag=0,x=0;char c='/';
 11     while(c<'0'||c>'9'){c=getchar();if(c=='-')flag=1;}
 12     while(c>='0'&&c<='9')x=x*10+(c-48),c=getchar();
 13     if(flag)n=-x;else n=x;
 14 }
 15 const int MAXN=200001;
 16 int n,m,bgx,bgy;
 17 int rudu[MAXN];
 18 struct node
 19 {
 20     int u,v,w,nxt;
 21 }edge[MAXN];
 22 int num=1;
 23 int head[MAXN];
 24 int flag[MAXN];// 記錄每個值是否能夠到達終點 
 25 int cs[MAXN];
 26 int dis[MAXN];
 27 int vis[MAXN];
 28 void add_edge(int ll,int rr,int ww)
 29 {
 30     edge[num].u=ll;
 31     edge[num].v=rr;
 32     edge[num].w=ww;
 33     edge[num].nxt=head[ll];
 34     head[ll]=num++;
 35 }
 36 void bfs()
 37 {
 38     queue<int>q;
 39     int tot=0;
 40     q.push(bgx),tot++;
 41     while(q.size()!=0)
 42     {
 43         int p=q.front();
 44         q.pop();
 45         for(int i=head[p];i!=-1;i=edge[i].nxt)
 46         {
 47             int to=edge[i].v;
 48             if(cs[to]++)continue;
 49             q.push(to);
 50         }
 51     }
 52     //rudu[bgy]=0;
 53     for(int i=1;i<=n;i++)
 54         if(rudu[i]!=cs[i]&&i!=bgy)
 55             flag[i]=1;
 56 }
 57 void dele()
 58 {
 59     for(int i=1;i<=num;i++)
 60     {
 61         if(flag[edge[i].u]!=0)
 62         {
 63             edge[i].u=-1;
 64             edge[i].v=-1;
 65             edge[i].w=-1;
 66             edge[i].nxt=-1;
 67         }
 68     }
 69 }
 70 void spfa()
 71 {
 72     queue<int>q;
 73     q.push(bgx);
 74     dis[bgx]=0;
 75     while(q.size()!=0)
 76     {
 77         int p=q.front();
 78         q.pop();
 79         vis[p]=0;
 80         for(int i=head[p];i!=-1;i=edge[i].nxt)
 81         {
 82             if(edge[i].u==-1)continue;
 83             int to=edge[i].v;
 84             if(dis[to]>dis[p]+edge[i].w)
 85             {
 86                 dis[to]=dis[p]+edge[i].w;
 87                 if(vis[to]==0)
 88                 {
 89                     vis[to]=1;
 90                     q.push(to);
 91                 }
 92             }
 93         }
 94     }
 95     if(dis[bgy]==INF)
 96     printf("-1");
 97     else
 98     printf("%d",dis[bgy]);
 99 }
100 int main()
101 {
102     freopen("roadb.in","r",stdin);
103     freopen("roadb.out","w",stdout);
104     read(n);read(m);
105     for(int i=1;i<=n;i++)head[i]=-1,dis[i]=INF;
106     for(int i=1;i<=m;i++)
107     {
108         int x,y;
109         read(x);read(y);
110         add_edge(y,x,1);
111         rudu[x]++;
112     }
113     read(bgy);read(bgx);
114     bfs();
115     dele();
116     spfa();
117     return 0;
118 }