Stanford coursera Andrew Ng 機器學習課程編程作業（Exercise 2）及總結

Exercise 1：Linear Regression 實現一個線性回歸關於如何實現一個線性回歸，請參考：http://www.cnblogs.com/hapjin/p/6079012.html Exercise 2：Logistic Regression 實現一個邏輯回歸問題描述：用邏輯回歸 ...

Exercise 1：Linear Regression---實現一個線性回歸

關於如何實現一個線性回歸，請參考：http://www.cnblogs.com/hapjin/p/6079012.html

Exercise 2：Logistic Regression---實現一個邏輯回歸

問題描述：用邏輯回歸根據學生的考試成績來判斷該學生是否可以入學。

這裡的訓練數據(training instance)是學生的兩次考試成績，以及TA是否能夠入學的決定（y=0表示成績不合格，不予錄取；y=1表示錄取）

因此，需要根據trainging set 訓練出一個classification model。然後，拿著這個classification model 來評估新學生能否入學。

訓練數據的成績樣例如下：第一列表示第一次考試成績，第二列表示第二次考試成績，第三列表示入學結果（0--不能入學，1--可以入學）

34.62365962451697, 78.0246928153624,  0
30.28671076822607, 43.89499752400101, 0
35.84740876993872, 72.90219802708364, 0
60.18259938620976, 86.30855209546826, 1
....
....
....

訓練數據圖形表示如下：橫坐標是第一次考試的成績，縱坐標是第二次考試的成績，右上角的 + 表示允許入學，圓圈表示不允許入學。（分數決定命運，太悲慘了！）

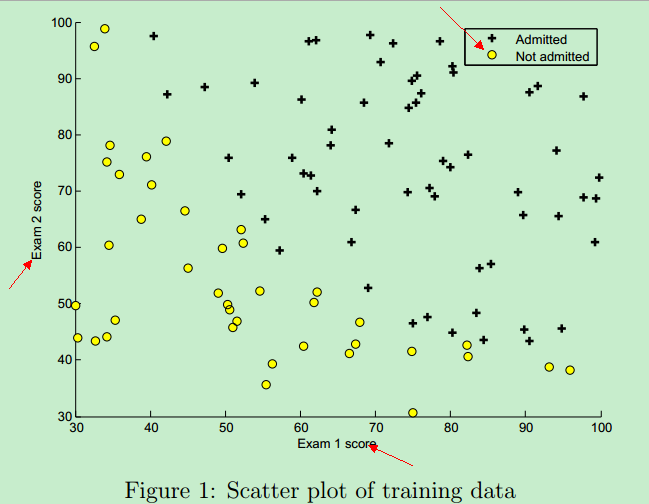
該訓練數據的圖形可以通過Matlab plotData函數畫出來,它調用Matlab中的plot函數和find函數，Matlab代碼實現如下：

function plotData(X, y)
%PLOTDATA Plots the data points X and y into a new figure 
%   PLOTDATA(x,y) plots the data points with + for the positive examples
%   and o for the negative examples. X is assumed to be a Mx2 matrix.
% Create New Figure

figure; hold on;

% ====================== YOUR CODE HERE ======================
% Instructions: Plot the positive and negative examples on a
%               2D plot, using the option 'k+' for the positive
%               examples and 'ko' for the negative examples.
%

pos = find(y==1);
neg = find(y==0);
plot(X(pos, 1), X(pos, 2), 'k+', 'LineWidth', 2, 'MarkerSize', 7);
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', 'MarkerSize', 7);
% =========================================================================

hold off;
end

Matlab載入數據：

%% Load Data
%  The first two columns contains the exam scores and the third column
%  contains the label.

data = load('ex2data1.txt'); 
X = data(:, [1, 2]); y = data(:, 3);% 矩陣 X 取數據的所有行的第一列和第二列，向量 y 取數據的第三列

由上面代碼可知：Matlab將文本文件中的訓練數據載入到矩陣X 和向量 y 中

載入完數據之後，執行以下代碼（調用自定義的plotData函數），將圖形畫出來：

plotData(X, y);

% Put some labels 
hold on;
% Labels and Legend
xlabel('Exam 1 score') %標記圖形的 X 軸
ylabel('Exam 2 score') %標記圖形的 Y 軸

% Specified in plot order
legend('Admitted', 'Not admitted') %圖形的右上角標簽
hold off;

圖形畫出來之後，對訓練數據就有了一個大體的可視化的認識了。接下來就要實現模型了，這裡需要訓練一個邏輯回歸模型。

①sigmoid function

對於 logistic regression而言，它針對的是 classification problem。這裡只討論二分類問題，比如上面的“根據成績入學”，結果只有兩種：y==0時，成績未合格，不予入學；y==1時，可入學。即，y的輸出要麼是0，要麼是1

如果採用 linear regression，它的假設函數是這樣的：

假設函數的取值即可以遠遠大於1，也可以遠遠小於0，並且容易受到一些特殊樣本的影響。比如在上圖中，就只能約定：當假設函數大於等於0.5時；預測y==1，小於0.5時，預測y==0。

而如果引入了sigmoid function，就可以把假設函數的值域“約束”在[0, 1]之間。總之，引入sigmoid function，就能夠更好的擬合分類問題中的數據，即從這個角度看：regression model 比 linear model 更合適 classification problem.

引入sigmoid後，假設函數如下：

sigmoid function 用Matlab 實現如下：

function g = sigmoid(z)
%SIGMOID Compute sigmoid functoon
%   J = SIGMOID(z) computes the sigmoid of z.

% You need to return the following variables correctly 
g = zeros(size(z));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the sigmoid of each value of z (z can be a matrix,
%               vector or scalar).

g = 1./(ones(size(z)) + exp(-z)); % ‘點除’ 表示 1 除以矩陣(向量)中的每一個元素

% =============================================================

end

②模型的代價函數(cost function)

什麼是代價函數呢？

把訓練好的模型對新數據進行預測，那預測結果有好有壞。因此，就用cost function 來衡量預測的"準確性"。cost function越小，表示測的越準。這裡的代價函數的本質是”最小二乘法“---ordinary least squares

代價函數的最原始的定義是下麵的這個公式：可見，它是關於 theta 的函數。(X，y 是已知的，由training set 中的數據確定了)

那如何求解 cost function的參數 theta，從而確定J(theta)呢？有兩種方法：一種是梯度下降演算法(Gradient descent)，另一種是正規方程(Normal Equation)，本文只討論Gradient descent。

而梯度下降演算法，本質上是求導數(偏導數)，或者說是：方嚮導數。方嚮導數所代表的方向--梯度方向，下降得最快。

而我們知道，對於某些圖形所代表的函數，它可能有很多個導數為0的點，這類函數稱為非凸函數(non-convex function)；而某些函數，它只有一個全局唯一的導數為0的點，稱為 convex function，比如下圖：

convex function能夠很好地讓Gradient descent尋找全局最小值。而上圖左邊的non-convex就不太適用Gradient descent了。

就是因為上面這個原因，logistic regression 的 cost function被改寫成了下麵這個公式：

可以看出，引入log 函數（對數函數），讓non-convex function 變成了 convex function

再精簡一下cost function，其實它可以表示成：

J(theta)可用向量表示成：

其Matlab語言表示公式如下：

J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m);

③梯度下降演算法

上面已經講到梯度下降演算法本質上是求偏導數，目標就是尋找theta，使得 cost function J(theta)最小。公式如下：

上面對theta(j)求偏導數，得到的值就是梯度j，記為：grad(j)

通過線性代數中的矩陣乘法以及向量的乘法規則，可以將梯度grad表示成向量的形式：

至於如何證明的，可參考：Exercise 1：Linear Regression---實現一個線性回歸

其Matlab語言表示公式如下：

grad = ( X' * ( sigmoid(X*theta)-y ) )/m; % X 為 training set 中的 feature variables, y 為training instance(訓練樣本的結果)結果

需要註意的是：對於logistic regression，假設函數h(x)=g(z)，即它引入了sigmoid function.

最終，Matlab中costfunction.m如下：

function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
%   J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
%   parameter for logistic regression and the gradient of the cost
%   w.r.t. to the parameters.

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Note: grad should have the same dimensions as theta
%

%J = (log(theta'*X')*y + (1-y)*log(1-theta'*X'))/(-m);
%attention matlab's usage
J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m);

% theta = theta - (alpha/m)*X'*(X*theta-y);
grad = ( X' * ( sigmoid(X*theta)-y ) )/m;

% =============================================================

end

通過調用costfunction.m文件中定義的coustFunction函數，從而運行梯度下降演算法找到使代價函數J(theta)最小化的邏輯回歸模型參數theta。調用costFunction函數的代碼如下：

%% ============= Part 3: Optimizing using fminunc  =============
%  In this exercise, you will use a built-in function (fminunc) to find the
%  optimal parameters theta.

%  Set options for fminunc
options = optimset('GradObj', 'on', 'MaxIter', 400);

%  Run fminunc to obtain the optimal theta
%  This function will return theta and the cost 
[theta, cost] = ...
    fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

從上面代碼的最後一行可以看出，我們是通過 fminunc 調用 costFunction函數，來求得 theta的，而不是自己使用 Gradient descent 在for 迴圈求導來計算 theta。for迴圈中求導計算theta，可參考：Exercise 1：Linear Regression---實現一個線性回歸

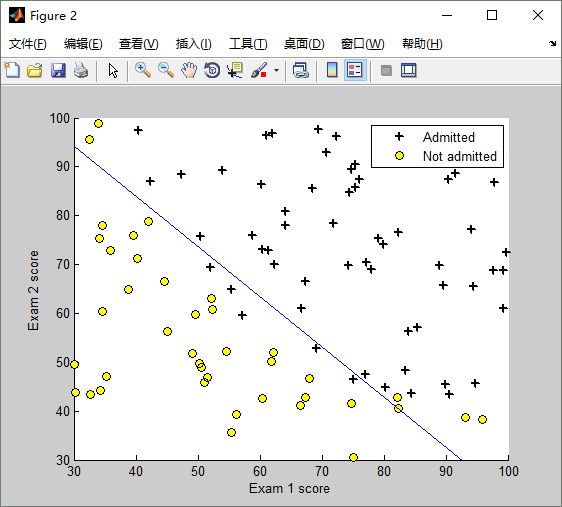
既然已經通過Gradient descent演算法求得了theta，將theta代入到假設函數中，就得到了 logistic regression model，用圖形表示如下：

④模型的評估（Evaluating logistic regression）

那如何估計，求得的邏輯回歸模型是好還是壞呢？預測效果怎麼樣？因此，就需要拿一組數據測試一下，測試代碼如下：

%% ============== Part 4: Predict and Accuracies ==============
%  After learning the parameters, you'll like to use it to predict the outcomes
%  on unseen data. In this part, you will use the logistic regression model
%  to predict the probability that a student with score 45 on exam 1 and 
%  score 85 on exam 2 will be admitted.
%
%  Furthermore, you will compute the training and test set accuracies of 
%  our model.
%
%  Your task is to complete the code in predict.m

%  Predict probability for a student with score 45 on exam 1 
%  and score 85 on exam 2 

prob = sigmoid([1 45 85] * theta); %這是一組測試數據，第一次考試成績為45，第二次成績為85
fprintf(['For a student with scores 45 and 85, we predict an admission ' ...
         'probability of %f\n\n'], prob);

% Compute accuracy on our training set
p = predict(theta, X);% 調用predict函數測試模型

fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);

fprintf('\nProgram paused. Press enter to continue.\n');
pause;

模型的測試結果如下：

For a student with scores 45 and 85, we predict an admission probability of 0.774323

Train Accuracy: 89.000000

那predict函數是如何實現的呢？predict.m 如下：

function p = predict(theta, X)
%PREDICT Predict whether the label is 0 or 1 using learned logistic 
%regression parameters theta
%   p = PREDICT(theta, X) computes the predictions for X using a 
%   threshold at 0.5 (i.e., if sigmoid(theta'*x) >= 0.5, predict 1)

m = size(X, 1); % Number of training examples

% You need to return the following variables correctly
p = zeros(m, 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters. 
%               You should set p to a vector of 0's and 1's
%
p = X*theta >= 0;

% =========================================================================

end

非常簡單，只有一行代碼：p = X * theta >= 0，原理如下：

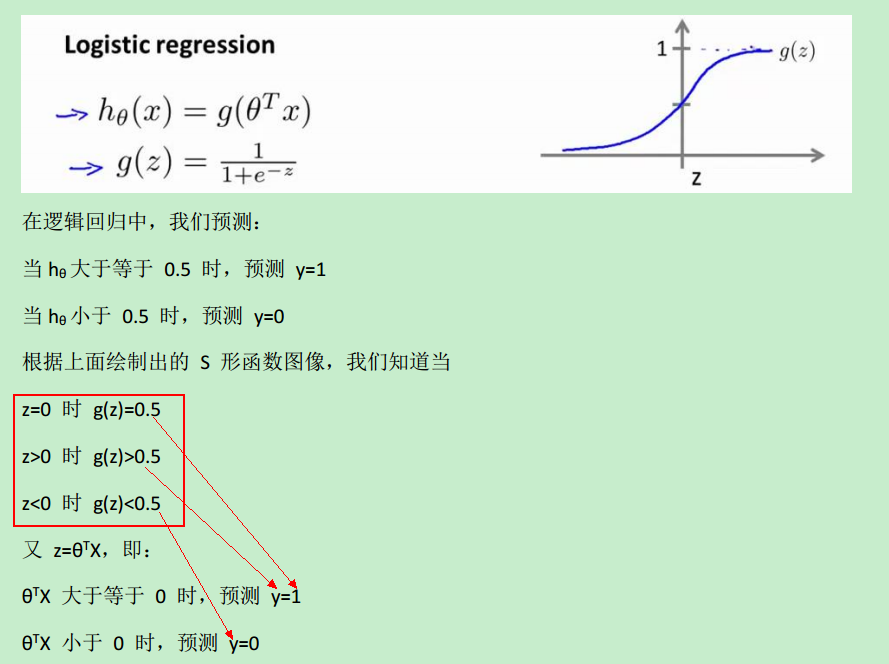
當h(x)>=0.5時，預測y==1，而h(x)>=0.5 等價於 z>=0

⑤邏輯回歸的正則化（Regularized logistic regression）

為什麼需要正則化？正則化就是為瞭解決過擬合問題(overfitting problem)。那什麼又是過擬合問題呢？

一般而言，當模型的特征(feature variables)非常多，而訓練的樣本數目(training set)又比較少的時候，訓練得到的假設函數(hypothesis function)能夠非常好地匹配training set中的數據，此時的代價函數幾乎為0。下圖中最右邊的那個模型就是一個過擬合的模型。

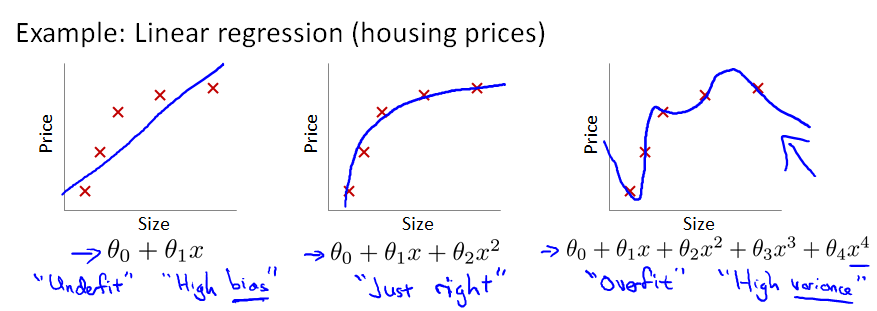
所謂過擬合，從圖形上看就是：假設函數曲線完美地通過中樣本中的每一個點。也許有人會說：這不正是最完美的模型嗎？它完美地匹配了traing set中的每一個樣本呀！

過擬合模型不好的原因是：儘管它能完美匹配traing set中的每一個樣本，但它不能很好地對未知的 (新樣本實例)input instance 進行預測呀！通俗地講，就是過擬合模型的預測能力差。

因此，正則化(regularization)就出馬了。

前面提到，正是因為 feature variable非常多，導致 hypothesis function 的冪次很高，hypothesis function變得很複雜(彎彎曲曲的)，從而通過穿過每一個樣本點(完美匹配每個樣本)。如果添加一個"正則化項"，減少高冪次的特征變數的影響，那 hypothesis function不就變得平滑了嗎？

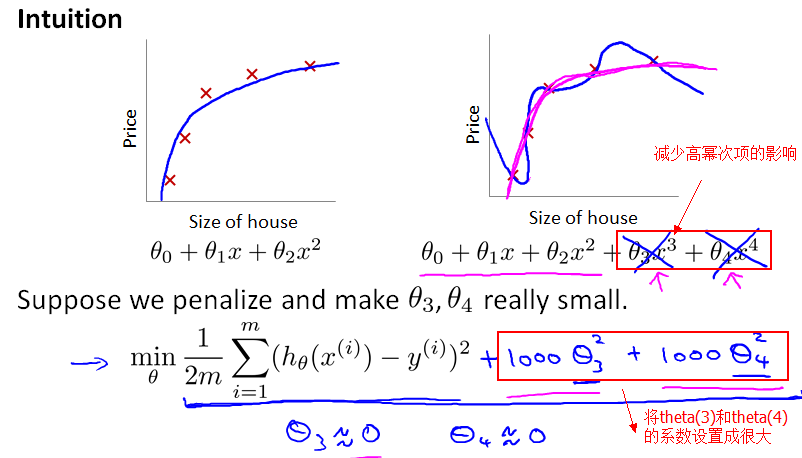
正如前面提到，梯度下降演算法的目標是最小化cost function，而現在把 theta(3) 和 theta(4)的繫數設置為1000，設得很大，求偏導數時，相應地得到的theta(3) 和 theta(4) 就都約等於0了。

更一般地，我們對每一個theta(j)，j>=1，進行正則化，就得到了一個如下的代價函數：其中的 lambda(λ)就稱為正則化參數(regularization parameter)

從上面的J(theta)可以看出：如果lambda(λ)=0，則表示沒有使用正則化；如果lambda(λ)過大，使得模型的各個參數都變得很小，導致h(x)=theta(0)，從而造成欠擬合；如果lambda(λ)很小，則未充分起到正則化的效果。因此，lambda(λ)的值要合適。

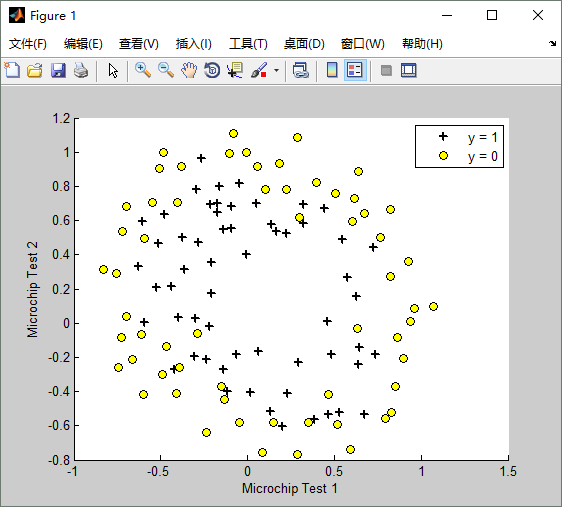
最後，我們來看一個實際的過擬合的示例，原始的訓練數據如下圖：

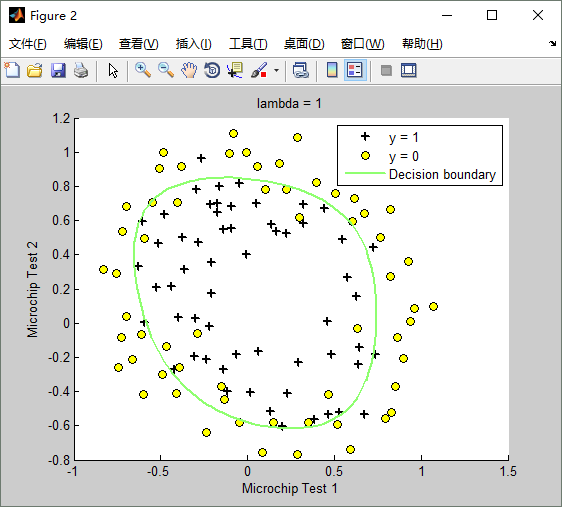
lambda(λ)==1時，訓練出來的模型（hypothesis function）如下：Train Accuracy: 83.050847

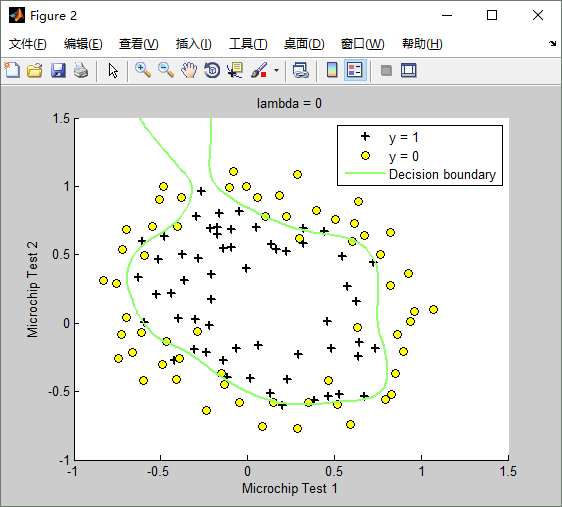
lambda(λ)==0時，不使用正則化，訓練出來的模型（hypothesis function）如下：Train Accuracy: 87.288136

lambda(λ)==100時，訓練出來的模型（hypothesis function）如下：Train Accuracy: 61.016949

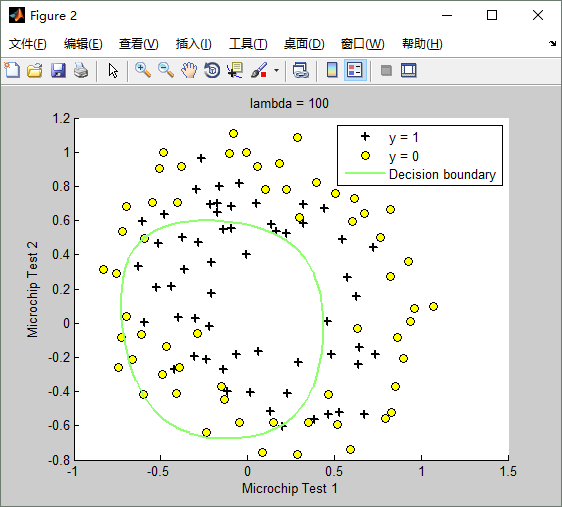
Matlab正則化代價函數的實現文件costFunctionReg.m如下：

function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
%   J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m);
%J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m) + (lambda / (2*m)) * (theta'*theta);
J = ( log( sigmoid(theta'*X') ) * y + log( 1-sigmoid(theta'*X') ) * (1 - y) )/(-m) + (lambda / (2*m)) * ( ( theta( 2:length(theta) ) )' * theta(2:length(theta)) );
%grad = ( X' * ( sigmoid(X*theta)-y ) )/m;
grad = ( X' * ( sigmoid(X*theta)-y ) )/m + ( lambda / m ) * ( [0; ones( length(theta) - 1 , 1 )].*theta );

% =============================================================

end

調用costFunctionReg.m的代碼如下：

%% ============= Part 2: Regularization and Accuracies =============
%  Optional Exercise:
%  In this part, you will get to try different values of lambda and 
%  see how regularization affects the decision coundart
%
%  Try the following values of lambda (0, 1, 10, 100).
%
%  How does the decision boundary change when you vary lambda? How does
%  the training set accuracy vary?
%

% Initialize fitting parameters
initial_theta = zeros(size(X, 2), 1);

% Set regularization parameter lambda to 1 (you should vary this)
lambda = 1;

% Set Options
options = optimset('GradObj', 'on', 'MaxIter', 400);

% Optimize
[theta, J, exit_flag] = ...
    fminunc(@(t)(costFunctionReg(t, X, y, lambda)), initial_theta, options);

% Plot Boundary
plotDecisionBoundary(theta, X, y);
hold on;
title(sprintf('lambda = %g', lambda))

% Labels and Legend
xlabel('Microchip Test 1')
ylabel('Microchip Test 2')

legend('y = 1', 'y = 0', 'Decision boundary')
hold off;

% Compute accuracy on our training set
p = predict(theta, X);

fprintf('Train Accuracy: %f\n', mean(double(p == y)) * 100);

⑥總結：

本文是對Stanford Machine Learning課程中的logistic regression的總結。結合課後編程習題，對logistic regression 各個知識點和編程作業中的代碼、實現原理作了詳細的解釋。

有興趣並且有時間學一名新技術是一件幸福的事情。

原文：http://www.cnblogs.com/hapjin/p/6078530.html