二叉排序樹

定義

---

• 若左子樹非空，則左子樹上所有結點關鍵字值均小於根節點關鍵字值
• 若右子樹非空，則右子樹上所有節點關鍵字值均大於根節點關鍵字值
• 左，右子樹分別是一顆二叉排序樹

二叉排序樹插入

---

二查排序樹插入定義:若原二叉樹為空，則直接插入節點。否則，若關鍵字K小於根節點關鍵字，則插入到左子樹中。若關鍵字K大於根節點關鍵字，則插入到右子樹當中。插入的時間複雜度是樹高O(H)

public void insert(Node p, int k) {
        if (p != null) {
            if (k < p.val)
                if (p.LChild == null) {
                    p.LChild = new Node();
                    p.LChild.val = k;
                } else
                    insert(p.LChild, k);
            else {
                if (p.RChild == null) {
                    p.RChild = new Node();
                    p.RChild.val = k;
                } else
                    insert(p.RChild, k);
            }
        }
}

二叉排序樹的刪除

---

刪除分三種情況：

• 如果被刪除的節點是葉子節點，就直接刪除
• 如果被刪除的節點只有左子樹或右子樹，則將其左子樹或右子樹代替該節點
• 如果左右子樹都存在，那麼則將其右子樹中序遍歷的第一個節點First替換該節點(值替換)，並將First從樹中刪除
• 刪除節點的時間複雜度為O(H)

public void delete(int k) {
        Node parent = new Node();
        parent.LChild = node;
        Node p = node;
        Node t = null;
        // 找出欲刪除的節點P
        while (p != null && p.val != k) {
            parent = p;
            if (k < p.val)
                p = p.LChild;
            else
                p = p.RChild;
        }
        // 欲刪節點的左右孩子都不為空
        if (p.LChild != null && p.RChild != null) {
            // 找出p的後繼節點(中序遍歷)
            Node post = inOrderFisrt(p.RChild);
            // 將後繼節點值copy給p
            p.val = post.val;
            // 將欲刪除的節點修改為post節點
            p = post;
        }
        // 欲刪節點的左孩子或右孩子為空
        if (p.LChild == null)
            t = p.RChild;
        else if (p.RChild == null)
            t = p.LChild;
        if (p == parent.LChild)
            parent.LChild = t;
        else
            parent.RChild = t;
    }

中序遍歷查找第一個節點

private Node inOrderFisrt(Node t) {
        Node p = null;
        while (t != null) {
            p = t;
            t = t.LChild;
        }
        return p;
    }

二叉排序樹構造

在構造二查排序樹時，只需要不斷調用二叉排序樹的插入演算法即可。下麵的代碼是不斷從一個數組中取出欲插入的數，然後調用insert方法將其插入到二叉樹當中。

private void initBST(Node node, int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            insert(node, arr[i]);
        }
    }

二叉排序樹的查找

---

查找演算法用遞歸實現，每次查找時都與根節點進行比較，如果小於根節點，則往左子樹上走。否則，向右子樹上走。

public Node search(Node p, int k) {
        if (p != null) {
            if (p.val == k)
                return p;
            else {
                if (k > p.val)
                    return search(p.RChild, k);
                else
                    return search(p.LChild, k);
            }
        } else
            return null;
    }

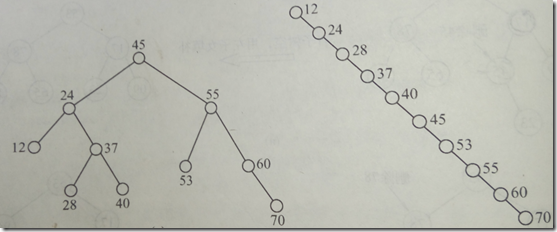
查找效率分析

---

二叉排序樹的查找效率和樹的構造有關。如果樹的左右子樹高度相當，那麼查找效率為O(logN),否則效率就很低，最低為O(N)。列如下麵兩棵樹，同樣找節點70，則左邊的效率明顯比右邊的高。