摘要:在 "迷宮問題求解之“窮舉+回溯”(一)" 這篇文章中採用“窮舉+回溯”的思想,雖然能從迷宮的入口到出口找出一條簡單路徑,但是找出來的不是最優路徑。因此本文采用A 搜索演算法,求解迷宮問題的最優路徑。 1 A 搜索演算法簡介 A 搜索演算法是一種啟髮式搜索演算法。所謂啟髮式搜索演算法,就是在盲目搜索演算法 ...
摘要:在迷宮問題求解之“窮舉+回溯”(一)這篇文章中採用“窮舉+回溯”的思想,雖然能從迷宮的入口到出口找出一條簡單路徑,但是找出來的不是最優路徑。因此本文采用A*搜索演算法,求解迷宮問題的最優路徑。
1 A*搜索演算法簡介
A*搜索演算法是一種啟髮式搜索演算法。所謂啟髮式搜索演算法,就是在盲目搜索演算法中加入一個啟發函數,在當前節點搜索完畢後,通過這個啟發函數來進行計算,選擇代價最少的節點作為下一步搜索的節點。通過這樣的方式就能夠找到最優解。
DFS,BFS這兩種搜索方式都屬於盲目的搜索方式,它不會在選擇下一個節點的時候進行代價計算,而是按照一個固定的方式選擇,這樣在運氣不好的情況,會對所有節點進行遍歷。
A*搜索演算法的核心就在於如何設計一個好的啟發函數,啟發函數的表達形式一般如下:
$$
f(n)=g(n)+h(n)
$$
其中$f(n)$是每個節點可能的估值或者代價值,它由兩部分組成。
- $g(n)$:它表示從起點到搜索點的代價。
- $h(n)$:它表示從搜索點到目標點的代價,$h(n)$設計的好壞,直接影響到該A*演算法的效率。
一種具有$f(n)=g(n)+h(n)$策略的啟髮式演算法能成為A*演算法的充分條件是:
搜索樹上存在著從起始點到終了點的最優路徑。
問題域是有限的。
所有結點的子結點的搜索代價值都大於零。
$h(n)=<h(n)$ ($h(n)$為實際問題的代價值)。
很顯然,1,2,3點都很容易滿足的。關鍵是設計一個好的$h(n)$函數。
2 A*搜索演算法描述
A*演算法的流程如下:
A*搜索演算法需要兩個額外的存儲空間,OPEN表和CLOSE表。
初始化OPEN和CLOSE表,將開始節點(開始節點的H和G的值都視為0)放入OPEN表中。
重覆下麵步驟:
(迴圈)2.1 在開始列表中查找具有最小F值的節點,並把查找到的節點作為當前節點;
2.2 把當前節點從OPEN列表中刪除,並加入到CLOSE列表中;
2.3 對當前節點相鄰的每一個節點依次執行以下步驟:
(遍歷)i 如果相鄰節點不可通行或者該節點已經在CLOSE列表中,則什麼操作也不執行; ii 如果該相鄰節點不在OPEN列表中,則將該節點添加到OPEN列表中,並將該相鄰節點的父節點設置當前節點,同時計算保存相鄰節點的F值;iii 如果該相鄰節點在OPEN表中, 則判斷若經由當前節點到達該相鄰節點的F值是否小於原來保存的F值,若小於,則將該相鄰節點的父節點設為當前節點,並重新設置該相鄰節點的F值.2.4 若當終點節點被加入到開發列表作為待檢驗節點時,表示路徑已找到,此時應終止迴圈;若當開放列表為空,表示沒有中開始節點到終點節點的路徑,此時迴圈結束;
迴圈終止後,從終點節點開始沿著父節點往前遍歷,從後到前輸出搜索的路徑。
其中,步驟2.3 ii中的紅色部分尤為重要,設置相鄰節點的父節點為當前節點是為了記錄從起始節點到終止節點路徑,方便搜索到了終點節點後進行路徑輸出。
在採用A* 演算法對迷宮路徑求解中,$g(n)$和$h(n)$函數都採用曼哈頓距離,曼哈頓距離代表兩個點在標準坐標繫上的絕對軸距總和。
$$
d(i,j)=|x1-x2|+|y1-y2|
$$
即每次獲取的當前通道塊,都會對其到入口通道快和出口通道塊的曼哈頓距離進行計算。求算當前通道塊的F值進行保存。該函數滿足啟髮式演算法成為A*演算法的充分條件的1,2,3,4。
還需要註意的一點是:使用A*求解迷宮路徑演算法中,需要把2.3步驟下麵的遍歷操作進行更改,如下:
i 如果相鄰節點不可通行或者該節點已經在CLOSE或者OPEN列表中,則什麼操作也不執行。
ii 如果該相鄰節點不在OPEN和CLOSE列表中,則將該節點添加到OPEN列表中,
並將該相鄰節點的父節點設置當前節點,同時計算保存相鄰節點的F值。
在迷宮求解中使用A*搜索演算法不需要去更新OPEN表中的已存在節點的F值,因為每個節點的位置都是確定的,所以曼哈頓距離就固定的。如果是帶權值的路網求解最短路徑,那麼就需要去更新OPEN表中節點的F值,如Dijkstra演算法。
3 程式實現
下麵使用使用c#語言,實現A*演算法求解迷宮最優的路徑。關鍵代碼如下:
3.1 節點實體類
class PathNode
{
public PathNode(int row, int col)
{
this.Row = row;
this.Col = col;
}
public int Row;
public int Col;
public int F=int.MaxValue;
public PathNode Father=null;//該節點的前繼節點
}3.2 A*搜索類
class AStartSolution
{
int [,]map;
int startX;
int startY;
int endX;
int endY;
public AStartSolution (int [,]map,int startX,int startY,int endX,int endY)
{
this.map=map;
this.startX =startX;
this.startY=startY;
this.endX=endX;
this.endY=endY ;
}
/*路徑尋找*/
public PathNode FindPath()
{
PathNode endNode = null;//終點
List<PathNode> openList = new List<PathNode>();
List<PathNode> closeList = new List<PathNode>();
//把起點放入open列表中
PathNode startNode = new PathNode(startX, startY);
openList.Add(startNode);
int tryCount = 0;
while (openList.Count != 0)
{
tryCount++;
PathNode curMinFNode = GetMinFPathNode(openList);
openList.Remove (curMinFNode );//從open列表中移除
closeList .Add (curMinFNode );//加入到close列表中
if (curMinFNode.Row == endX && curMinFNode.Col == endY)//當前節點是目標節點
{
endNode = curMinFNode;
break;
}
else//搜索4個方向併進行處理
{
//東
HandleChildNode(curMinFNode, curMinFNode.Row, curMinFNode.Col + 1, openList, closeList);
//南
HandleChildNode(curMinFNode, curMinFNode.Row+1, curMinFNode.Col, openList, closeList);
//西
HandleChildNode(curMinFNode, curMinFNode.Row, curMinFNode.Col-1, openList, closeList);
//北
HandleChildNode(curMinFNode, curMinFNode.Row-1, curMinFNode.Col, openList, closeList);
}
}
return endNode;
}
/*處理每個方向的子節點*/
private void HandleChildNode(PathNode curMinFNode,int row, int col, List<PathNode> openList, List<PathNode> closeList)
{
PathNode child = null;
if (Pass(row, col))//能通過
{
child = new PathNode(row, col);
if (!IsExistList(child, closeList) && !IsExistList(child, openList))//
{
child.F = GetF(row,col);
child.Father = curMinFNode;
openList.Add(child);
}
}
}
private PathNode GetMinFPathNode(List<PathNode> openList)
{
int minF= openList.Min(node =>node.F);
foreach (PathNode node in openList)
{
if (node.F == minF)
{
return node;
}
}
return null;
}
/*該通道塊是否可通行*/
private bool Pass(int row,int col)
{
int rowCount = map.GetLength(0);
int colCount = map.GetLength(1);
//邊界判斷
if (row >= 0 && row < rowCount && col >= 0 && col < colCount)
{
//障礙判斷
if (map[row, col] == 2)
{
return false;
}
else
{
return true;
}
}
else
{
return false;
}
}
/*當前通道塊是否在OPEN或者CLOSE表中*/
private bool IsExistList(PathNode childNode, List<PathNode> list)
{
foreach (PathNode node in list)
{
if (node.Row == childNode.Row && node.Col == childNode.Col)
{
return true;
}
}
return false;
}
/*計算當前節點的F值*/
private int GetF(int curRow, int curCol)
{
int g = Math.Abs(startX - curRow) + Math.Abs(startY - curCol);
int h = Math.Abs(endX - curRow) + Math.Abs(endY - curCol);
return g + h;
}
}3.3 與“窮舉+回溯”演算法的效果比較
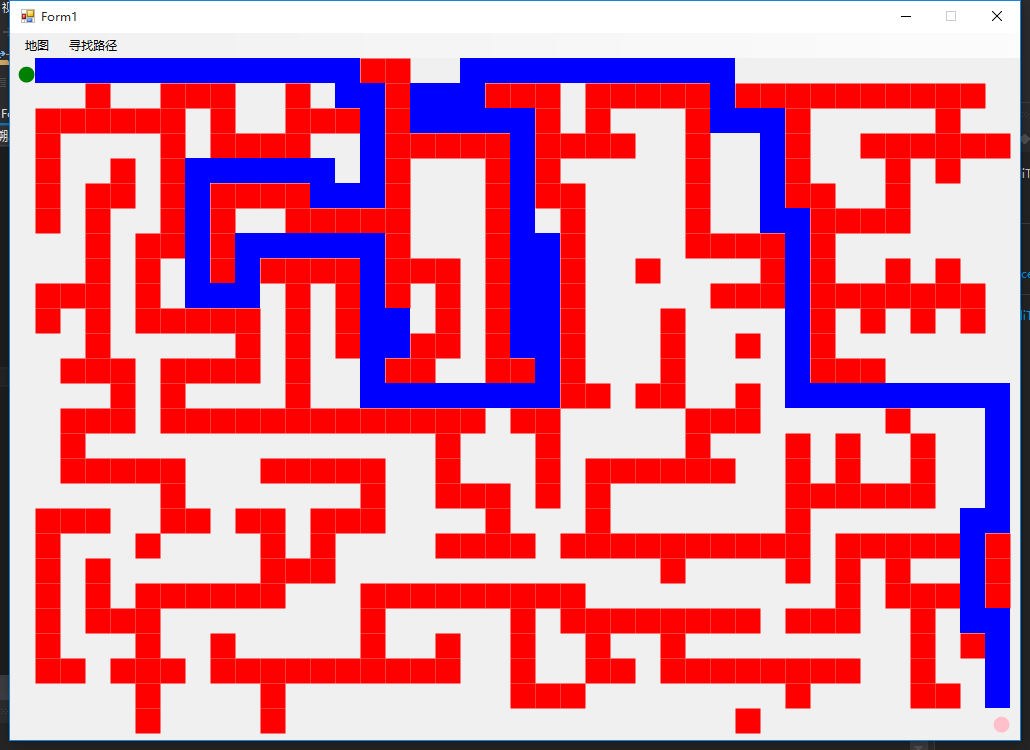
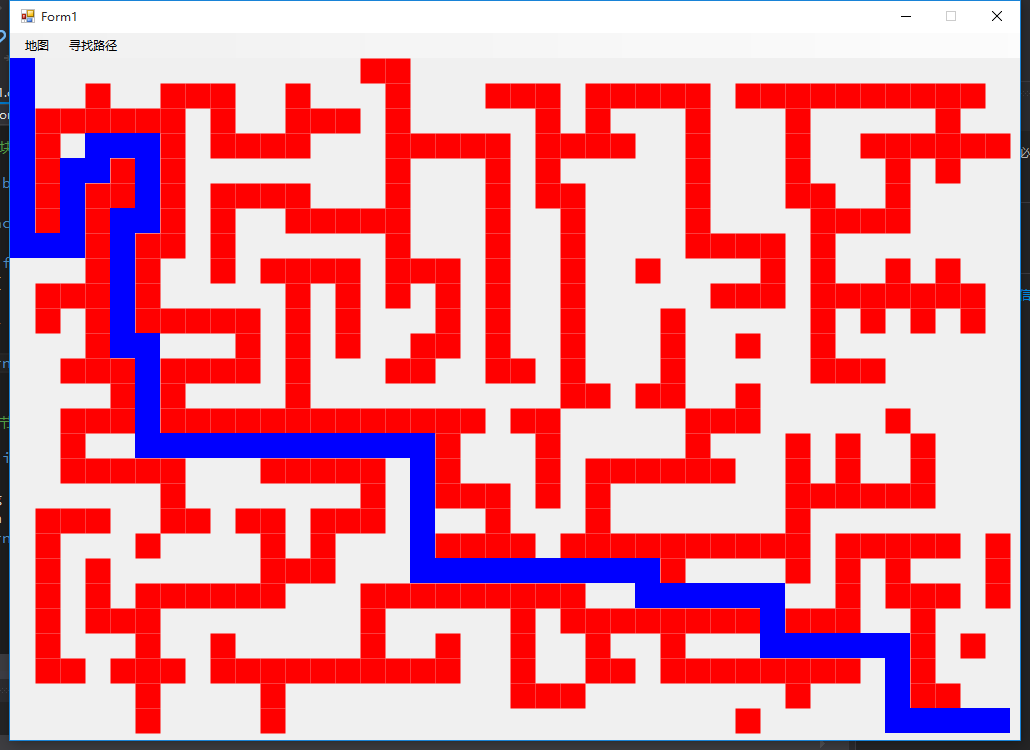
採用同樣的迷宮地圖比較兩種演算法查找的路徑,上結果圖代表“窮舉+回溯,下結果圖代表本程式。
4 總結
通過上面的比較可以發現,A*搜索演算法尋找的路徑比“窮舉+回溯”演算法的要短很多,和我設計迷宮地圖時所想的路徑是一致,是一條最優的路徑。
5 資源和參考資料
參考資料:
莫水千流的博文A星尋路演算法介紹
西芒xiaoP的博文A*搜索演算法
yueming的博文A*路徑尋找演算法入門
源碼地址:
http://download.csdn.net/download/mingge38/9655373



