求迷宮從入口到出口的所有路徑是一個經典的程式設計問題,求解迷宮,通常採用的是“窮舉+回溯”的思想,即從入口開始,順著某一個方向出發,若能夠走通,就繼續往前走;若不能走通,則退回原路,換一個方向繼續向前探索,直到所有的通路都探尋為止。因此本文依據這種“窮舉+回溯”的思想,設計一個求解迷宮的程式。 1 ...
求迷宮從入口到出口的所有路徑是一個經典的程式設計問題,求解迷宮,通常採用的是“窮舉+回溯”的思想,即從入口開始,順著某一個方向出發,若能夠走通,就繼續往前走;若不能走通,則退回原路,換一個方向繼續向前探索,直到所有的通路都探尋為止。因此本文依據這種“窮舉+回溯”的思想,設計一個求解迷宮的程式。
1 問題分析
為了保證在任何位置上都能夠退回原路,顯然需要使用一個先進後出的數據結構來保存已經探尋過的位置,因此在程式求解迷宮路徑的過程中採用棧這種數據結構。
迷宮是一個二維地圖,其中含有出口和入口,障礙點和通道,因此程式採用一個二位數組map來表示,其中,二維數組值所代表的含義如下:
0:通道 1:起點 2:障礙 3:終點 4:路徑需要註意的是,最後求解出來的通路,必須要是一條簡單路徑,即在求得的路徑上不能重覆出現同一通道快。下麵簡述一下程式的求解過程。
將“在搜索過程中某一個時刻所在迷宮地圖中的位置“記為“當前位置”,那麼求解迷宮路徑演算法的基本思想是:若“當前位置”可通行,那麼將“當前位置”納入求解路徑中(壓到棧中),並朝“下一個位置”繼續探索,即把“下一位置”切換到“當前位置”,如此重覆下去,直到找到出口;如果當前位置不可以通行,則順著來的方向退回到“前一個通道位置”,然後再朝著其他方向探索下去;如果該通道塊的4個方向(東西南北)都不可通,那麼就在該路徑(棧)中刪除該通道位置(刪除棧頂元素),再繼續退回到“前一個通道位置”繼續探索,即再獲取棧頂元素作為“當前位置繼續上述的重覆探索。
2 演算法描述
根據對迷宮問題的分析,求迷宮中一條從入口到出口的路徑演算法描述如下:
設定入口位置為當前位置。
if(當前位置是可通行且是沒有被走過的通道塊 )
(分支1)2.1 將當前位置壓到棧中。
2.2 若當前位置是出口,
則程式結束,返迴路徑棧。2.3 若當前不是出口,則切換當前位置為當前位置東邊的通道塊,
返回2繼續執行。else(若當前位置不可通行)
(分支2)3.1 獲取棧頂元素所在的位置,若該位置所在的相鄰4個方向都被探索過了,則刪除當前棧頂元素,獲取新的棧頂元素,直到找到一個可通的相鄰塊位置或出棧至棧空
再執行3.2步驟。3.2 若棧頂元素所在的位置還有其他方向沒有被探索過,則設定新的當前位置為棧頂元素的未被探索方向的相鄰通道塊。(方向訪問順序為順時針即東南西北)
重覆步驟2.
需要註意步驟2中的沒有被走過的通道塊,是指該通道塊從來未壓入棧中,否則求解的路徑就不是一條簡單路徑,很可能導致一個死迴圈。
3 程式實現
程式採用c#語言對上述的演算法描述進行了實現,代碼如下。
3.1 通到塊實體
class PathElement
{
public PathElement(int row, int col, int direcation)
{
this.Row = row;
this.Col = col;
this.Direction = direcation;
}
public int Row;//位置所在的行
public int Col;//位置所在的列
public int Direction;//從此位置走向下一位置的方向,方向分為東0南1西2北3,預設東方向為初始方向
}3.2 尋找簡單路徑
public static Stack<PathElement> FindPath(int[,] map, int startX, int startY, int endX, int endY)
{
Stack<PathElement> path = new Stack<PathElement>();
List<PathElement> visitedList = new List<PathElement>();//保存以通過的元素
PathElement curPosition = new PathElement(startX, startY, 0);
int tryCount = 0;
do
{
tryCount++;
if (Pass(curPosition, map) && (!Visited(curPosition, visitedList)))//當前位置能通過,且沒被訪問過
{
path.Push(curPosition);//加入路徑
if (curPosition.Row == endX && curPosition.Col == endY)
return path;
visitedList.Add(curPosition);//該位置以被訪問
curPosition = GetNextPosition(curPosition);//獲取下一個當前位置,並更新該位置的下一個位置的方向
}
else//當前不能通過
{
if (path.Count != 0) //如何棧不為空
{
PathElement topElement = path.Peek();//獲取棧頂元素
while (topElement.Direction == 4 && (path.Count > 1))//找尋一個可用的位置
{
path.Pop();
topElement = path.Peek();
}
if (topElement.Direction < 4)
{
curPosition = GetNextPosition(topElement);//獲取下一個當前位置,並更新該位置的下一個位置的方向
}
}
}
} while (path.Count != 0);
return null;
}3.3 輔助方法
/*獲取下一個位置*/
private static PathElement GetNextPosition(PathElement curPostion)
{
PathElement nextPosition=null;
switch (curPostion.Direction)
{
case 0:
nextPosition = new PathElement(curPostion.Row, curPostion.Col+1, 0);
break;
case 1:
nextPosition = new PathElement(curPostion.Row+1, curPostion.Col, 0);
break;
case 2:
nextPosition = new PathElement(curPostion.Row, curPostion.Col-1, 0);
break;
case 3:
nextPosition = new PathElement(curPostion.Row-1, curPostion.Col, 0);
break;
}
curPostion.Direction++;
return nextPosition;
}
/*是否為通道*/
private static bool Pass(PathElement curPosition, int[,] map)
{
int rowCount = map.GetLength(0);
int colCount = map.GetLength(1);
//邊界判斷
if (curPosition.Row >= 0 && curPosition.Row < rowCount && curPosition.Col >= 0 && curPosition.Col < colCount)
{
//障礙判斷
if (map[curPosition.Row, curPosition.Col] == 2)
{
return false;
}
else
{
return true;
}
}
else
{
return false;
}
}
/*是否被訪問*/
private static bool Visited(PathElement curPosition, List<PathElement> visitedList)
{
foreach (PathElement element in visitedList)
{
if (element.Row == curPosition.Row && element.Col == curPosition.Col)
{
return true;
}
}
return false;
}3.4 界面
該部分代碼只是提供演算法驗證的可視化界面,與本文所探討的演算法實現沒有多大的關係,程式的源代碼可以在文章後面的鏈接進行下載。
界面所包含的功能:
- 能夠編輯迷宮地圖,單擊實現障礙物的設計,雙擊去掉障礙物。
- 能夠保存和載入地圖。
- 能夠通過該演算法實現從迷宮入口到出口路徑的生成和顯示。
3.5 結果截圖
1 地圖的載入

2 路徑尋找
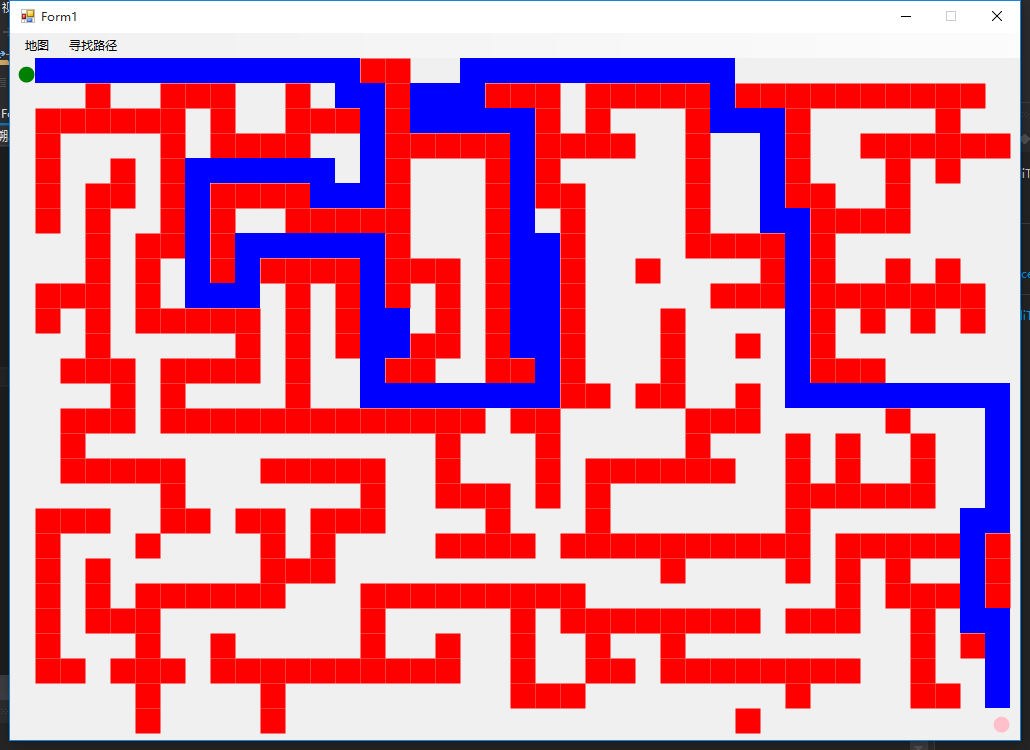
4 總結
“窮舉+回溯”的思路還是很好理解,通俗的講,就是選擇一條道路一直走到黑,如果碰到前方有障礙,就退回來一步再換一個方向繼續走,直到把所有可能的路都做完了。
利用“窮舉+回溯”搜索路徑,雖然簡單,但是它屬於一種盲目、機械的搜索演算法,從3.5中的結果圖中可以看出,該演算法找出來的路徑,顯然不是最優的,走了許多的彎路。那麼如何從迷宮的起點到終點找到一條最優的路徑呢?敬請期待《迷宮問題求解之“A*搜索”(二)》。
5 資源和參考資料
參考資料:嚴蔚敏《數據結構c語言版》
源代碼下載:http://download.csdn.net/detail/mingge38/9653205


