AcWing 演算法基礎課week 1 總結 總結點 1:快速排序(分治思想) 題1:從小到大排序 主體思路:定義一個數x屬於數組s,利用雙指針,將數組分為大於等於x和小於等於x的兩部分,然後遞歸處理。(具體步驟如下) 1. 如上圖所示,我們定義一個數組s用來儲存n個數據,然後定義兩個指針i j,分別 ...
AcWing 演算法基礎課week 1 總結
總結點 1:快速排序(分治思想)
題1:從小到大排序
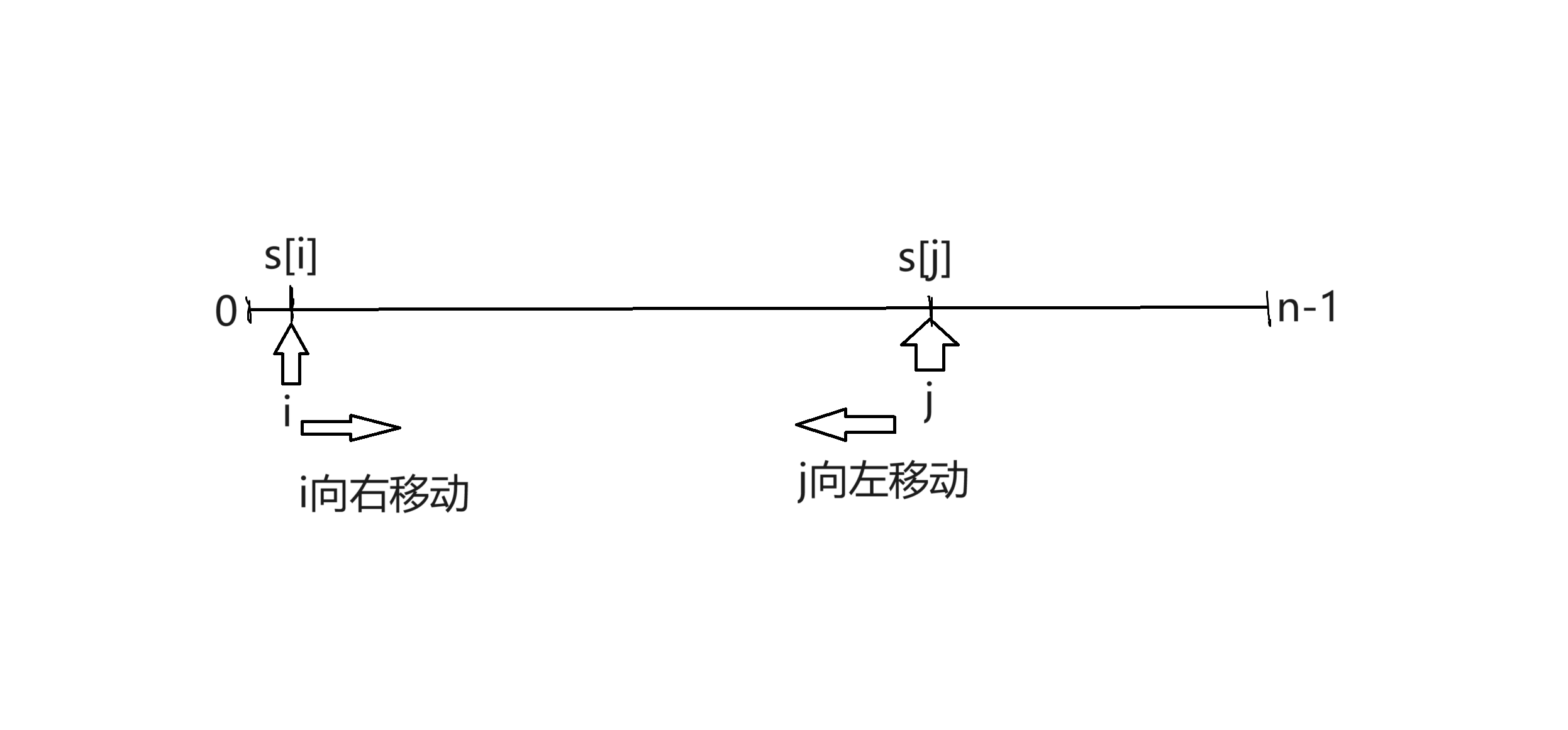
主體思路:定義一個數x屬於數組s,利用雙指針,將數組分為大於等於x和小於等於x的兩部分,然後遞歸處理。(具體步驟如下)
1.
如上圖所示,我們定義一個數組s用來儲存n個數據,然後定義兩個指針i j,分別指向數組的左右兩端,同時i指針逐個向右移動掃描數組,j指針同理向左。
2.
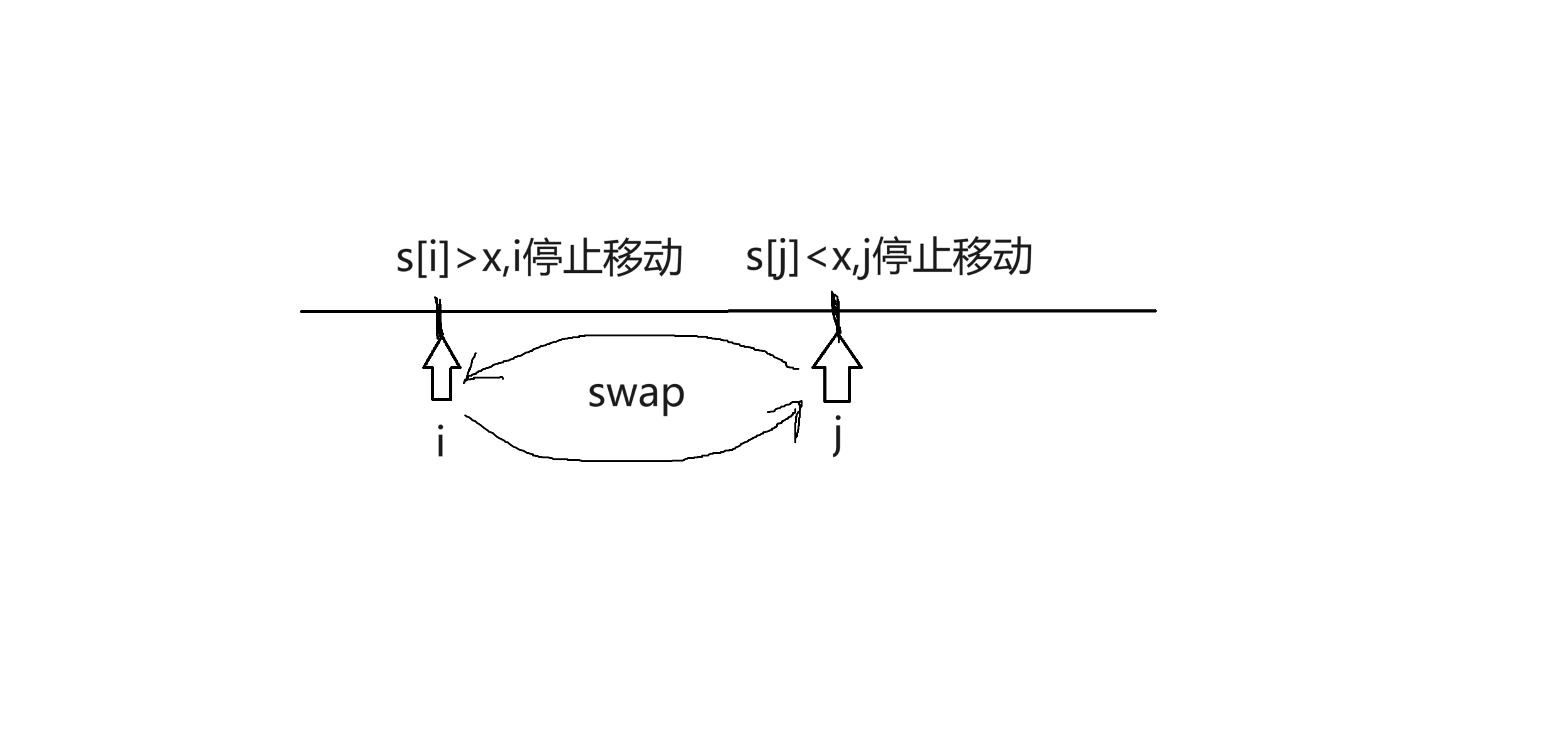
當i,j指針掃描的過程中,當s[i]>x時,指針i就停止移動,同理當s[j]<x時,指針j就停止移動,然後交換s[i]與s[j],那麼就使得大於x的s[i]去到了右邊的數組,小於x的s[j]去到了左邊的數組。
while(i<j)
{
do i++;while(s[i]<x);//i指針向右移動,當s[i]>x,移動停止,j同理
do j--;while(s[j]>x);
if(i<j)swap(s[i],s[j]);//如果i<j說明s[j]<x<s[i],就進行交換
}
3.
重覆以上操作,直到i>=j為止。然後相同的方式利用遞歸處理左右兩半邊的數組,直到子數組長度等於1。
quick_sort(s,l,j);
quick_sort(s,j+1;r);
完整代碼如下
int n;
int s[1000010];
void quick_sort(int s[], int l, int r)//將s[]數組的l-r區間內的數據排序
{
if (l >= r)return;
//以中點數據值作為分界值,避免邊界問題。
//註意:以s[l],s[r]作為分界值時需要考慮邊界問題,所以直接取中點値
int x = s[l + r >> 1], i = l - 1, j = r + 1;
while (i < j)
{
do i++; while (s[i] < x);//指針移動直到遇到不符合條件的值
do j--; while (s[j] > x);
if (i < j)swap(s[i], s[j]);//交換兩值
}
quick_sort(s, l, j);//遞歸處理左右兩邊
quick_sort(s, j + 1, r);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> s[i];
}
quick_sort(s, 0, n - 1);//將s[]數組的l-r區間內的數據排序
for (int i = 0; i < n; i++)
{
cout << s[i] << ' ';
}
return 0;
}
題2:找到第k小的數(快速排序的拓展)
主體思路與快排相同,只是遞歸方式不同。
掃描方式與快排相同,我們直接說不同點(遞歸);
當我們利用雙指針i,j掃描一個區間時,肯定會將一個區間分成兩部分,而我們需要找到第k個數,這個數可能在前半部分或者後半部分,所以我們分情況遞歸。
1.如果k在前一部分,就只遞歸前一部分
2.如果在後一部分,就遞歸後面
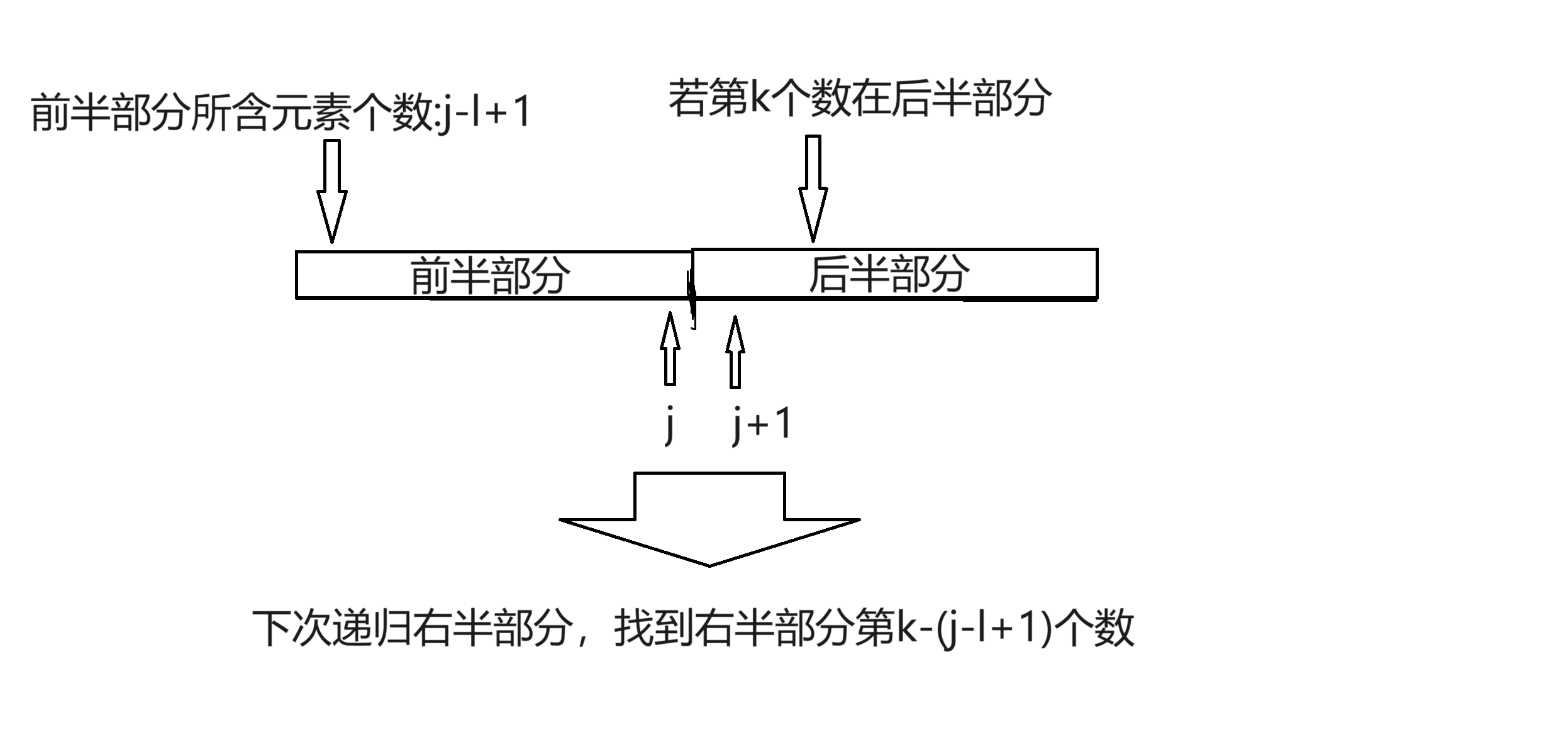
int sl = j-l+1;//sl記錄的是前一部分有多少個數
if(k<=sl) return quick_sort(s,l,j,k);
else return quick_sort(s,j+1,r,k-(j-l+1));
//註意我們這裡輸入的第四個變數是指所求數在某一區間的相對位置。
//如果在右邊,因為左邊部分已經有j-l+1個數了,所以我們應該找這一區間的第k-(j-l+1)個數
完整代碼:
int n, k;
vector<int> s;
int quick_sort(vector<int> s, int l, int r, int k)
{
if (l >= r)return s[l];//如果區間長度為1,返回0
int i = l - 1, j = r + 1, x = s[l + r >> 1];
while (i < j)
{
do i++; while (s[i] < x);
do j--; while (s[j] > x);
if (i < j)swap(s[i], s[j]);
}
int sl = j - l + 1;//計算左邊部分有多少個數
if (k <= sl)return quick_sort(s, l, j, k);//遞歸左邊
else return quick_sort(s, j + 1, r, k - (j - l + 1));//遞歸右邊
}
int main()
{
cin >> n >> k;
for (int i = 0; i < n; i++)
{
int x;
cin >> x;
s.push_back(x);
}
cout << quick_sort(s, 0, n - 1, k) << endl;
return 0;
}
總結點2:歸併排序(分治思想)
題1:排序
主體思路:將數組均分為兩半部分,分別有序化,然後合併兩個數組
1.
將數組均分為兩半部分,利用遞歸分別有序化。
int mid = l+r>>1;
merge_sort(s,l,mid);
merge_sort(s,mid+1,r);
2.
合併兩個數組。利用兩個指針i,j分別指向兩個數組的起始位置,如果s[i]<s[j]就將s[i]放入新數組,反之放入s[j]。
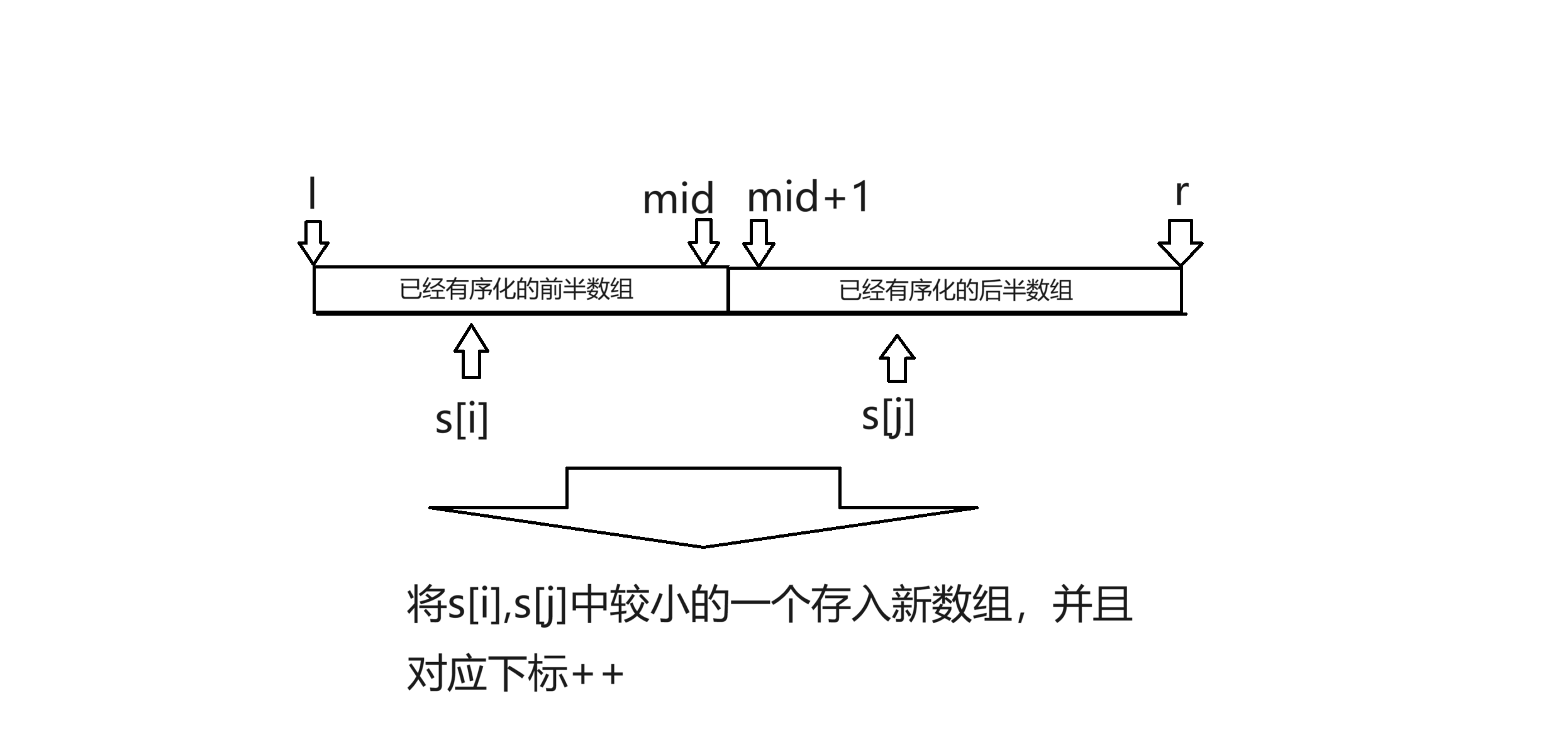
int temp[1000010];//新數組
int k = 0,i = l,j = mid+1;//k負責控制新數組的下標
while(i<=mid&&j<=r)
{
if(s[i]<s[j]) temp[k++] = s[i++];
else temp[k++] = s[j++];
}
3.
因為我們上面使用的迴圈條件時while(i<=mid&&j<=r),所以當一個數組中的全部元素全部放入新數組時,另一個數組可能會還有剩餘的數據,所以我們需要將這些數據也放入新數組中。
while(i<=mid) temp[k++] = s[i++];
while(l<=r) temp[k++] = s[j++];
4.
最後需要將新數組中的數據儲存回原數組中,因為遞歸的過程中需要再次用到原數組,所以必須儲存回去。
for(int i = l,j = 0;i<=r;i++,j++) s[i] = temp[j];//i控制原數組,j控制臨時數組
完整代碼如下:
int n;
int s[1000010];
void a(int s[], int l, int r)
{
if (l >= r)return;
int temp[1000010];
int mid = l + r >> 1;
a(s, l, mid);
a(s, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
{
if (s[i] < s[j])temp[k++] = s[i++];
else temp[k++] = s[j++];
}
while (i <= mid) temp[k++] = s[i++];
while (j <= r)temp[k++] = s[j++];
for (int i = l, j = 0; i <= r; i++, j++)
{
s[i] = temp[j];
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)cin >> s[i];
a(s, 0, n - 1);
for (int i = 0; i < n; i++)cout << s[i] << ' ';
return 0;
}
題2:逆序對的數量
主體思想:利用歸併排序的將兩個數組分別有序化後合併的特點,遞歸計算逆序對的數量
1.
因為思路同歸併排序,我們直接講不同點。
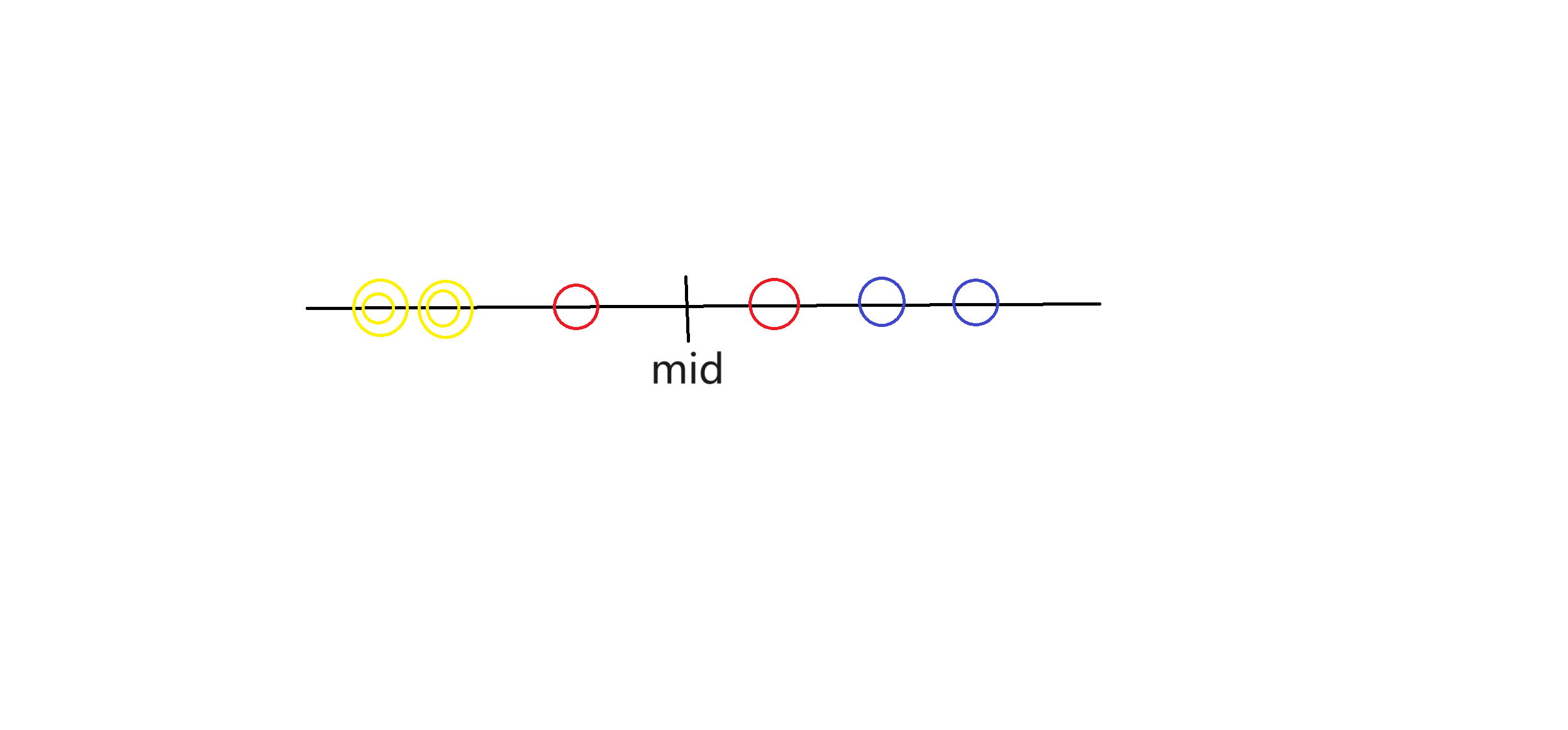
對於一組逆序對,可以分為圖中的三種情況:
1.同時在左側數組
2.同時在右側數組
3.分別在左右兩側數組
發現對於1,2種情況,當我們將數組進行遞歸排序時,總有一個區間可以使得兩個數分別在數組中點的左右兩側,從而轉化為第3種情況,所以我們只考慮第三種情況。
2.
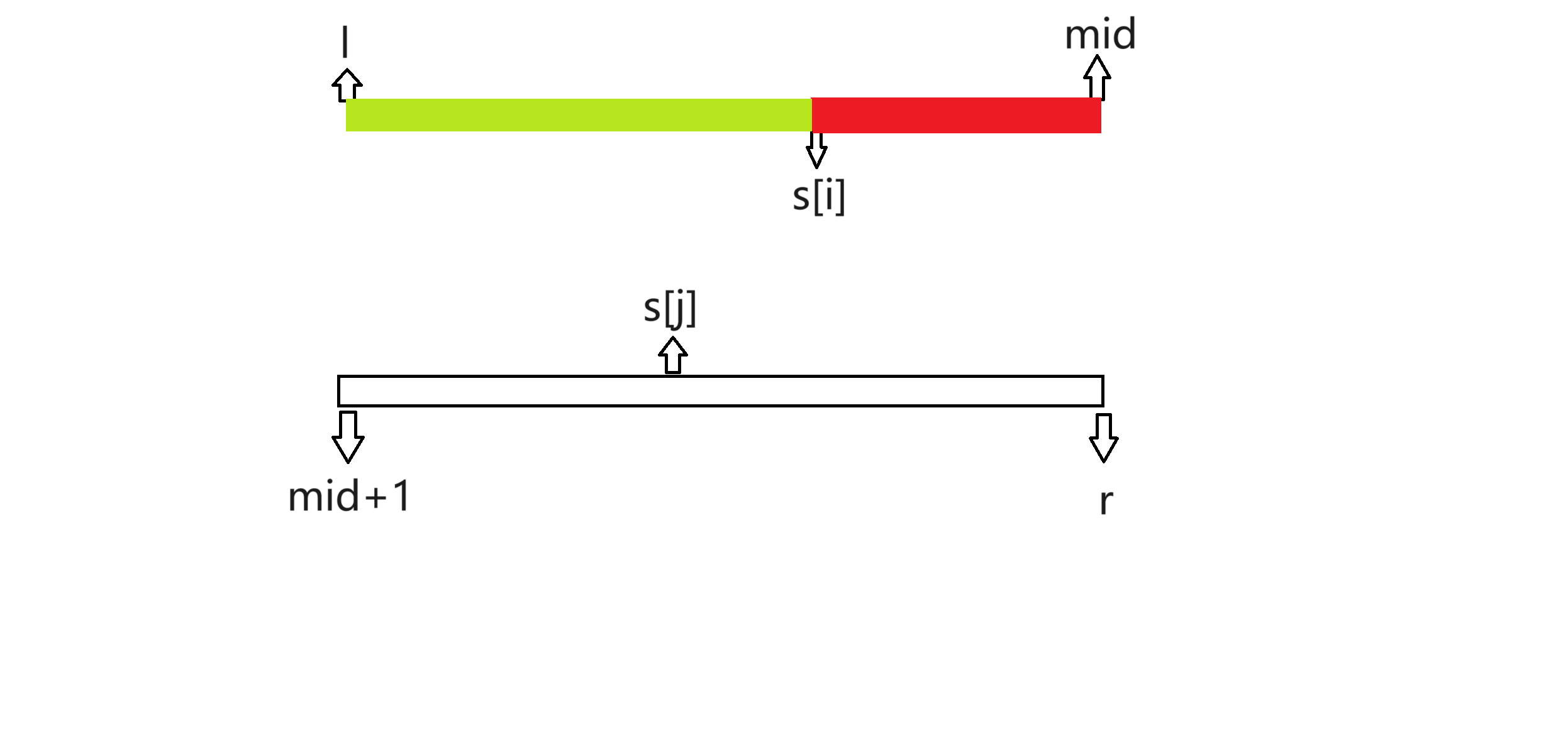
考慮圖中的情況,因為兩個數組都已經有序化,所以對於s[j]發現有s[i]到s[mid]的部分(圖中紅色部分)都大於s[j],所以後面的所有數都可與s[j]構成第三種逆序對,逆序對的數量為mid-i+1。
3.
完整代碼實現:
const int N = 100010;
int n;
int a[N];
long long ans;
long long merge_sort(int l, int r)
{
if (l >= r)return 0;
int mid = l + r >> 1;//中點
merge_sort(l, mid);//遞歸處理左右兩邊,是左右兩邊有序化
merge_sort(mid + 1, r);
int temp[N];//臨時數組
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
{
if (a[i] <= a[j])temp[k++] = a[i++];//將小的數放入臨時數組
else
{
temp[k++] = a[j++];
//如果s[i]>s[j],說明s[i]-s[mid]的數都與s[j]構成逆序對
//個數為mid-i+1
ans += mid - i + 1;
}
}
while (i <= mid) temp[k++] = a[i++];
while (j <= r)temp[k++] = a[j++];
for (int i = l, j = 0; i <= r; i++, j++)a[i] = temp[j];
return ans;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
cout << merge_sort(0, n - 1) << endl;
return 0;
}
總結點3:二分
直接講整數二分,浮點數二分只需要修改細節就好,後面會講
1.
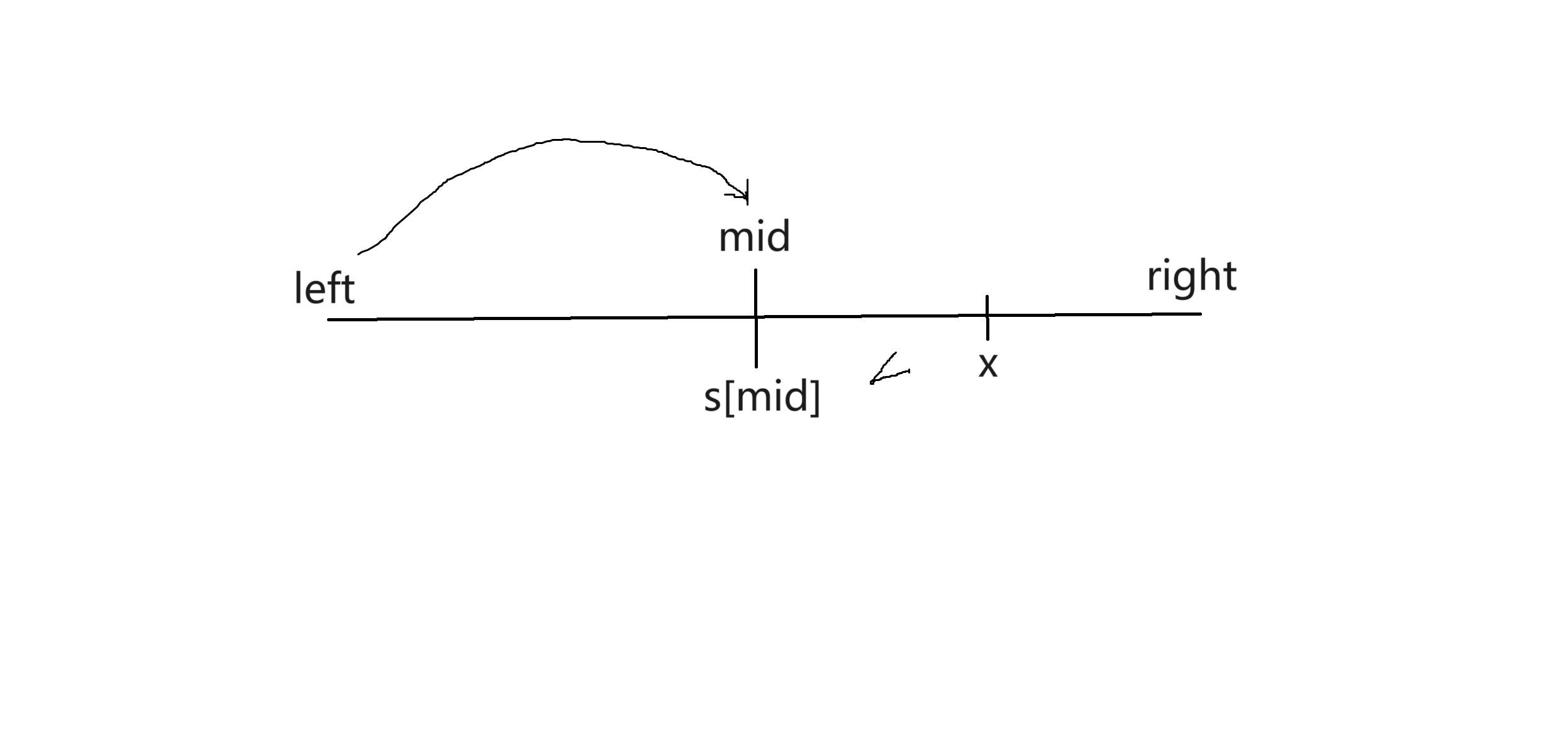
每次找到區間的中點,將s[mid]與x的值相比較。如果是圖中的這種情況,x>s[mid] ,所以x存在於右區間。那麼調整區間,將區間的左端點調整為mid+1(為什麼是mid+1後面會講),再去迴圈處理右區間。另一種情況同理。
2.
因為存在邊界問題,所以這裡的二分需要分情況討論,對應的代碼也有兩種。
首先是邊界調整的問題。重要的就是那邊可以取到最後的值x,就將哪邊的邊界調整為mid。直接看代碼講。(代碼題目是找到x在數組中的位置)
先看第一種
int l = 0,r = n-1//設置左右端點
while(l<r)
{
int mid = l+r>>1;//設置中點
if(s[mid]<=x) r = mid;
//註意此時x可以在這個判斷條件中取到,所以這個條件對應的邊界調整為mid
else l = mid+1;
//另一個對應的調整為mid+1或mid-1;
}
再看第二種
int l = 0,r = n-1;
while(l<r)
{
int mid = l+r+1>>1;
if(s[mid]<=x) l = mid;
//這時x可以在新的條件中取到,所以對應邊界調整為mid,其餘同理。
else r = mid-1;
}
3.
另外的,兩種情況所移動的方向不同。
當用第一種模版時,將會從數組左向右去找x的值,直到從左向右找到第一個數為止,此時的邊界l就是第一個x的位置。
當用第二種模版時,將會從右向左,直到找到一個數為止,l代表找到的第一個x的位置,註意使用這個模版時,mid = l+r+1>>1。
我們下麵看例題
題1:找到一個數的範圍
主體思路:利用第一種模版找到左邊界,然後利用第二種去找右邊界
看代碼:
int main()
{
int n, q;//n是數組長度,註意預設是升序排列,然後q個查詢
cin >> n >> q;
vector<int> s(n);
for (auto& n : s)
{
cin >> n;
}
while (q--)
{
int x;
cin >> x;
int l = 0, r = n - 1;//設置左右邊界
while (l < r)//找到左邊界
{
int mid = l + r >> 1;
if (s[mid] >= x)r = mid;
else l = mid + 1;
}
if (s[l] != x)//如果沒有X就輸出-1 -1
{
cout << "-1 -1" << endl;
}
else
{
cout << l << ' ';
l = 0; r = n - 1;
while (l < r)//找到右邊界
{
int mid = l + r +1>> 1;//註意+1的細節
if (s[mid] <= x)l = mid;
else r = mid - 1;
}
cout << l << endl;
}
}
return 0;
}
題2:數的三次方根
這個題就是浮點數二分,浮點數二分比整數二分簡單,因為沒有邊界條件,兩個值都去調整為mid。
不多說,直接看代碼:
double n;
bool check(double x)//利用check函數去判斷條件
{
return x * x * x < n;
}
int main()
{
cin >> n;
double l = -10000, r = 10000;//題目中給的左右邊界的範圍
while (fabs(r - l) > 1e-8)//浮點數相等的判斷
{
double mid = (l + r) / 2;
if (check(mid)) l = mid;//兩個都去調整為mid
else r = mid;
}
cout << fixed << setprecision(6) << l;//輸出6位小數
return 0;
}
總結點4:高精度
所有的高精度都是利用數組去儲存一個數,然後通過模擬手算的方式去計算。(之前有發過一期高精度,但是看了y神的代碼之後,決定去學習一下y神的代碼,很美觀)
1.高精度加法
高精加的主體思路就是將兩個數組的相同位置上的數字相加,如果大於10就進位。
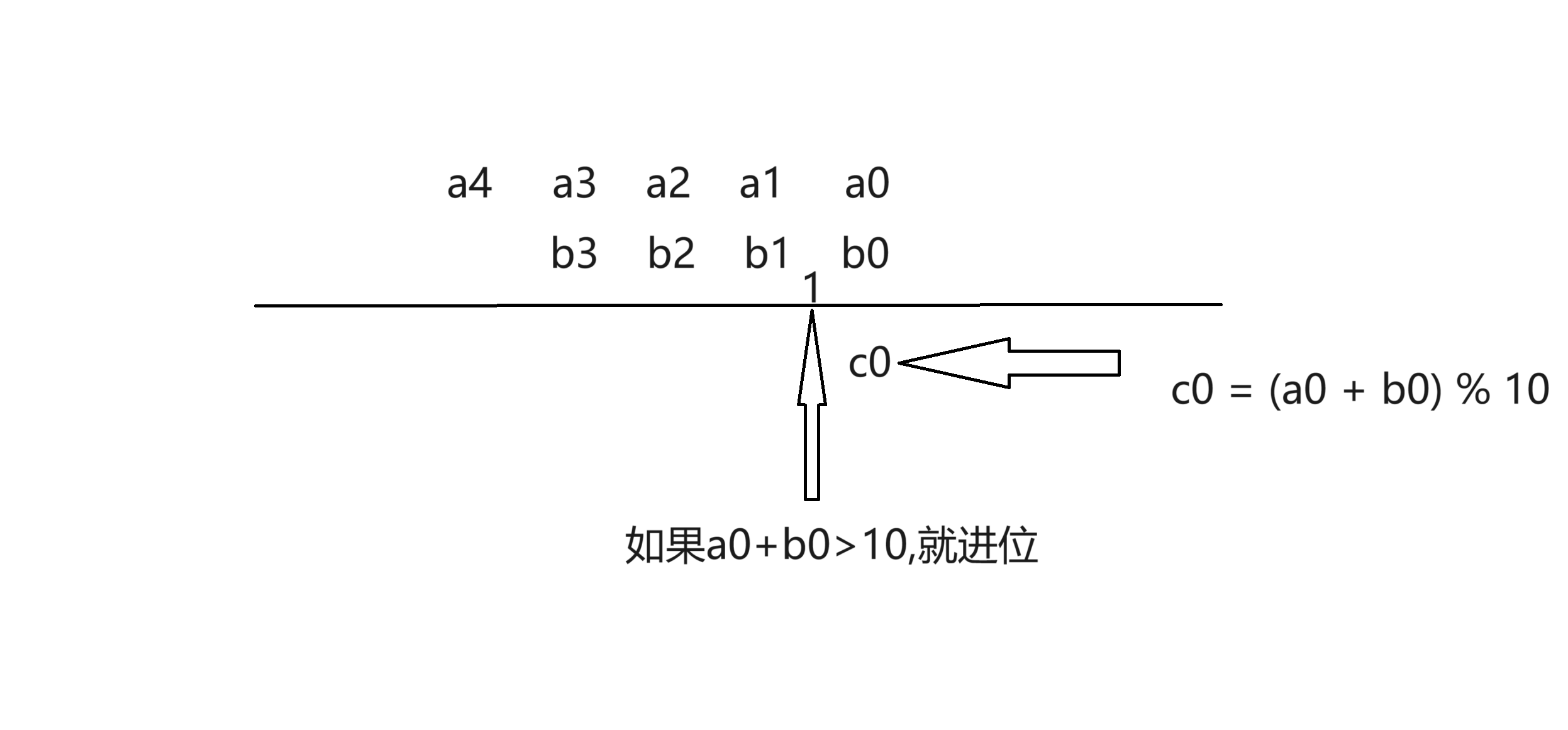
核心代碼看一下:
vector<int > c;
int t= 0;
for(int i = 0;i<max(a.size(),b.size());i++)
{
if(i<a.size()) t+=a[i];
if(i<b.size()) t+=b[i];
c.push_back(t%10);
t/=10;
}
if(t) c.push_back(t);
return c;
完整代碼如下:
string x, y;
vector<int> add(vector<int > a, vector<int> b)
{
vector<int> c;
int t = 0;
for (int i = 0; i < max(a.size(), b.size()); i++)
{
if (i < a.size())t += a[i];//如果a有這位數字,就加上
if (i < b.size())t += b[i];
c.push_back(t % 10);//每次將t的個位數輸入到c中
t /= 10;//保留t的10位進行下一次計算
}
if (t)c.push_back(t);//因為加法可能有進位,所以最後檢查一下進位
return c;
}
int main()
{
cin >> x >> y;
vector<int> a, b;
//兩個字元串倒序輸入到數組中
for (int i = x.size() - 1; i >= 0; i--)a.push_back(x[i] - '0');
for (int i = y.size() - 1; i >= 0; i--)b.push_back(y[i] - '0');
auto c = add(a, b);
//倒序輸出
for (int i = c.size() - 1; i >= 0; i--)cout << c[i];
return 0;
}
2.高精度減法
1.兩個數相減,如果小於0,就進位。
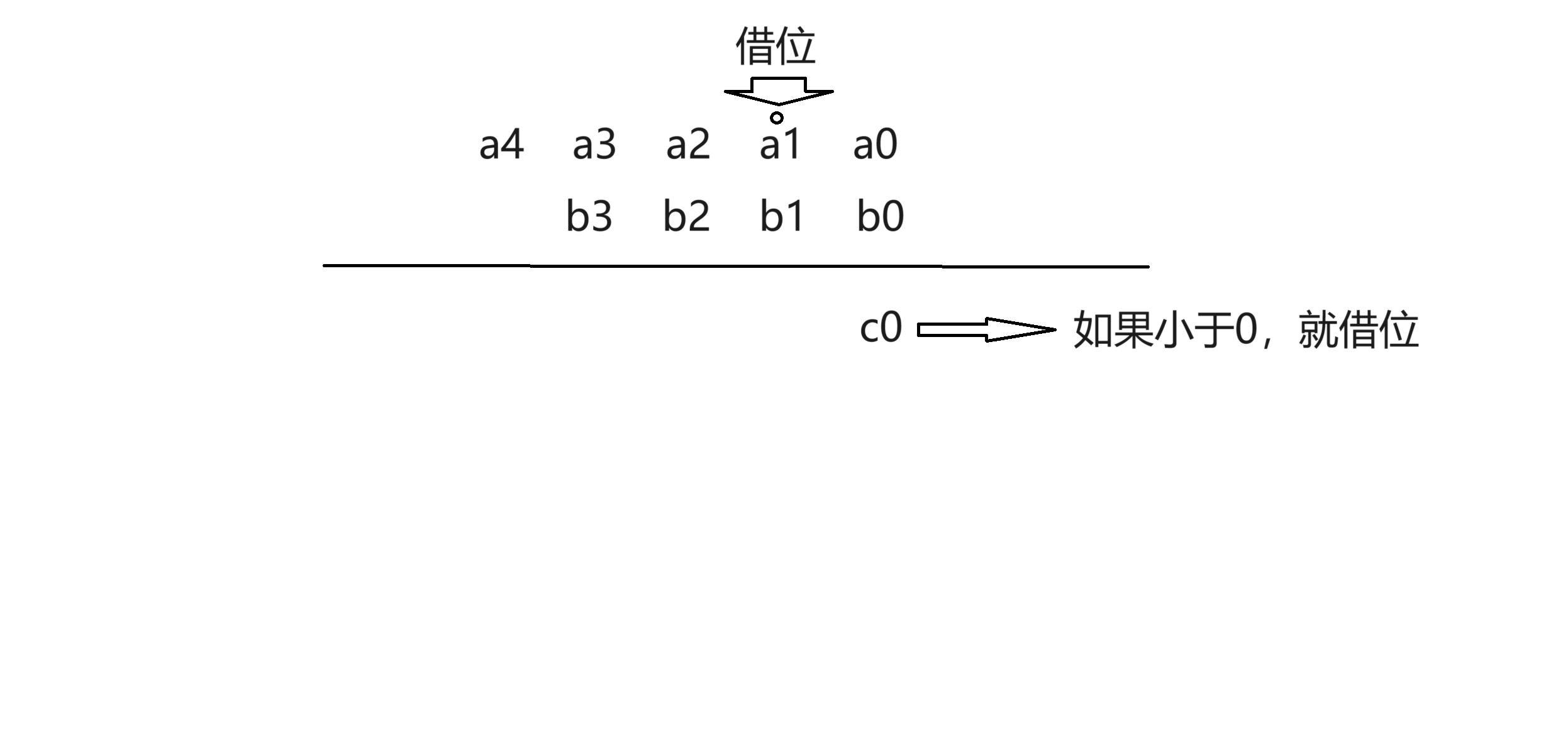
vector<int> c;
int t = 0;
for (int i = 0,t = 0; i < a.size(); i++)
{
t = a[i] - t;//t儲存的是上一位的借位,先減去。
if (i < b.size())t -= b[i];//如果b存在這位數,就減去
c.push_back((t + 10) % 10);
//減去之後,t有可能是負數需要借位,所以利用(t+10)%10,輸出借位後的結果
if (t < 0) t = 1;//如果t<10,就借位
else t = 0;
}
while (c.size() > 1 && c.back() == 0)c.pop_back();//除前導0
return c;
2.那麼到這裡就有問題了,上面的代碼我們只考慮了A>B的情況,那麼A-B<0時怎麼辦?
很簡單,只要用B-A,然後提起輸出一個負號就好啦。
那我們先判斷A是否大於B;
bool check(vector<int> a,vector<int> b)
{
//如果位數不一樣,位數多的大
if(a.size()!=b.size()) return a.size()>b.size();
//如果位數一樣,就從高位到低位逐位判斷
//因為我們倒序將字元串轉化為了數組,所以高位在最後面
for(int i = a,size()-1;i>=0;i--)
{
if(a[i]!=b[i]) return a[i]>b[i];
}
}
下麵是完整代碼:
string x, y;
bool cmp(vector<int> a, vector<int> b)//判斷大小
{
if (a.size() != b.size())return a.size() > b.size();
for (int i = a.size() - 1; i >= 0; i--)
{
if (a[i] != b[i])return a[i] > b[i];
}
return true;
}
vector<int> sub(vector<int> a, vector<int> b)
{
vector<int> c;
for (int i = 0,t = 0; i < a.size(); i++)
{
t = a[i] - t;
if (i < b.size())t -= b[i];
c.push_back((t + 10) % 10);
if (t < 0) t = 1;
else t = 0;
}
while (c.size() > 1 && c.back() == 0)c.pop_back();
return c;
}
int main()
{
cin >> x >> y;
vector<int > a, b;
for (int i = x.size() - 1; i >= 0; i--)a.push_back(x[i] - '0');
for (int i = y.size() - 1; i >= 0; i--)b.push_back(y[i] - '0');
if (cmp(a, b))//如果a>b,正常計算
{
auto c = sub(a,b);
for (int i = c.size() - 1; i >= 0; i--)cout << c[i];
}
else//如果b>a
{
auto c = sub(b, a);
cout << '-';//先輸出’-‘
//然後輸出b-a
for (int i = c.size() - 1; i >= 0; i--)cout << c[i];
}
}
3.高精度乘法(大數乘小數)
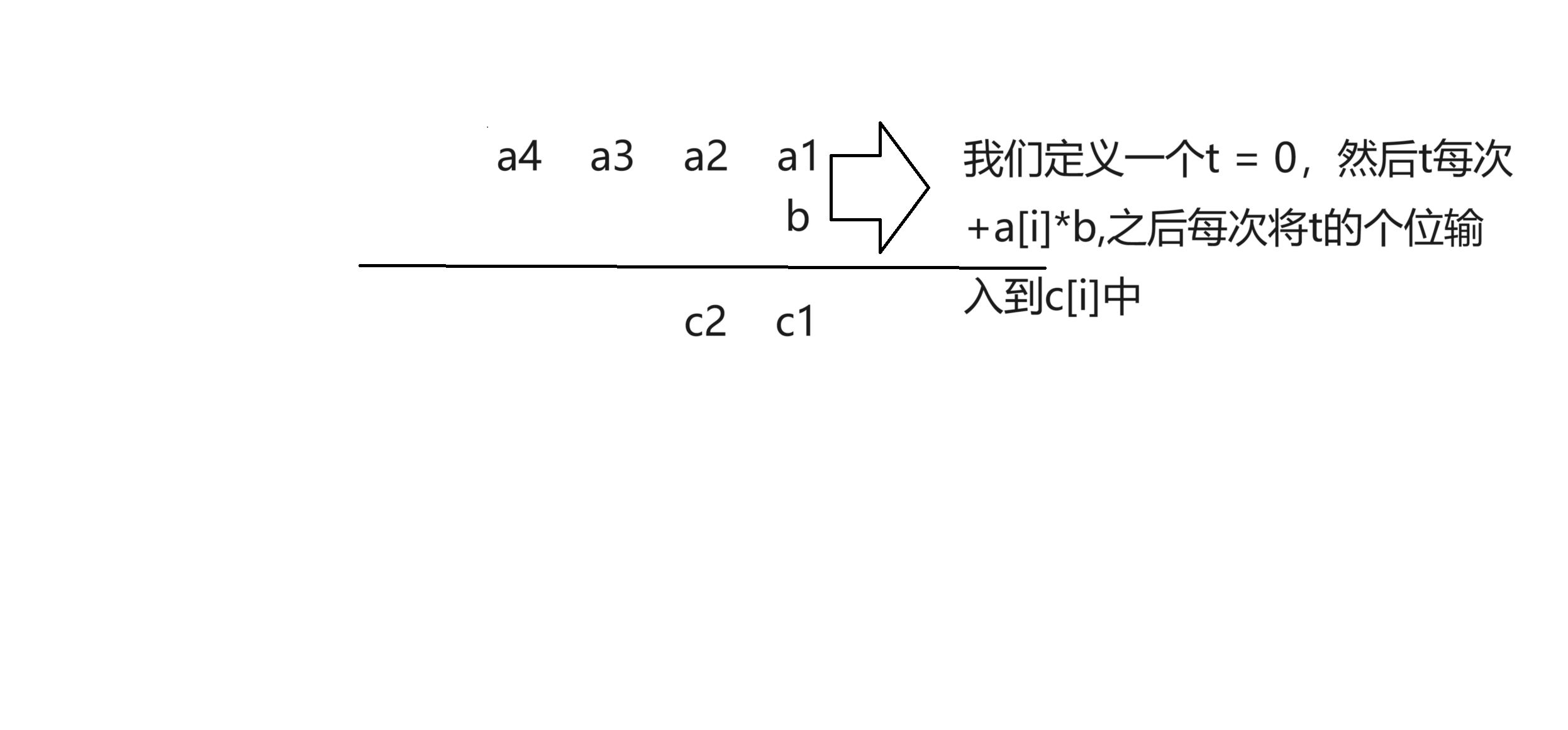
如圖示(利用的就是乘法與c[i]的規律,具體證明省略,如想看,請評論區提問),直接就得到核心代碼:
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
//註意迴圈條件
for (int i = 0, t = 0; i < a.size() || t; i++)//註意乘法時,當a被執行完後,t不一定為0,但還需要繼續將t輸入到c中
{
if (i < a.size())t += a[i] * b;//如果a有這位數,就t+=a[i]*b;
c.push_back(t % 10);//將t的個位輸入到c中
t /= 10;
}
while (c.size() > 1 && c.back() == 0)c.pop_back();//去除前導0
return c;
}
完整代碼如下:
string x;
int b;
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
for (int i = 0, t = 0; i < a.size() || t; i++)
{
if (i < a.size())t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while (c.size() > 1 && c.back() == 0)c.pop_back();
return c;
}
int main()
{
cin >> x >> b;
vector<int> a;
for (int i = x.size() - 1; i >= 0; i--)a.push_back(x[i] - '0');
auto c = mul(a, b);
for (int i = c.size() - 1; i >= 0; i--)cout << c[i];
return 0;
}
4.高精度除法
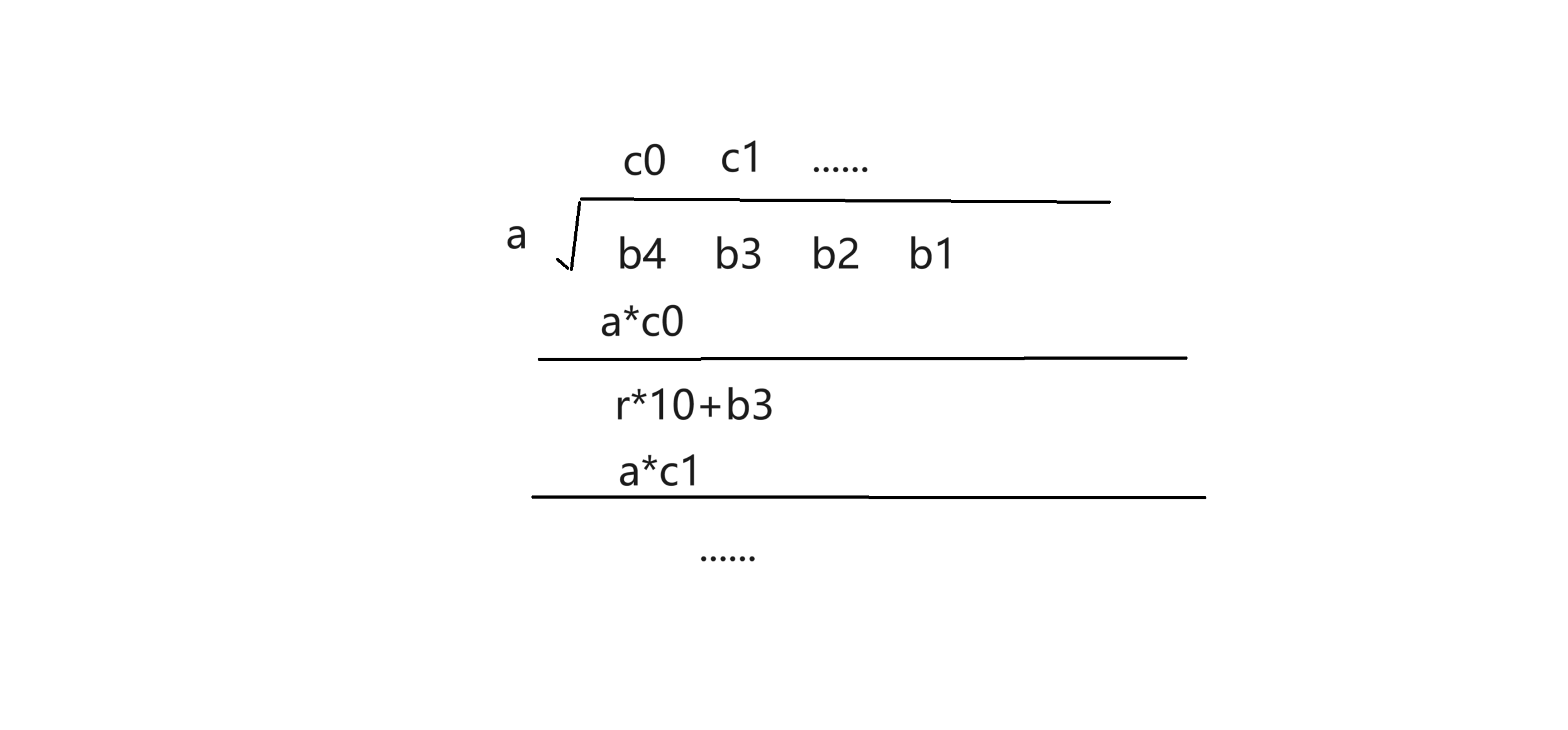
如圖,我們設定b數組為被除數,a為除數,r為餘數。
我們從b高位到低位進行計算,那麼第一個商c0就應該等於b[4]/a的商,然後餘數r就等於b[4]%a;
下一次的除數就等於r*10+b[i],反覆計算。
下麵看代碼實現:(因為我們要保證加減乘除的輸入方式統一,所以在輸入a數組時依舊是倒序輸入)
//代碼中的a與b與圖中的a,b相反。
vector<int> div(vector<int> &a, int &b,int &r)
{
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)//因為a是倒序輸入,但是除法需要從高位到低位進行計算,所以i = a.size()-1
{
r = r * 10 + a[i];//每一次的被除數等於r*10+a[i]
c.push_back(r / b);//商等於r/b;
r %= b;餘數等於r%b
}
reverse(c.begin(), c.end());//反轉之後消除前導0
while (c.size() > 1 && c.back() == 0)c.pop_back();
return c;
}
完整代碼如下:
vector<int> div(vector<int> &a, int &b,int &r)
{
vector<int> c;
for (int i = a.size() - 1; i >= 0; i--)
{
r = r * 10 + a[i];
c.push_back(r / b);
r %= b;
}
reverse(c.begin(), c.end());
while (c.size() > 1 && c.back() == 0)c.pop_back();
return c;
}
int main()
{
string x;
int b;
cin >> x >> b;
vector<int> a;
for (int i = x.size() - 1; i >= 0; i--)a.push_back(x[i] - '0');
int r = 0;
auto c = div(a, b,r);
for (int i = c.size() - 1; i >= 0; i--)
{
cout << c[i];
}
cout << endl << r << endl;
return 0;
}
總結點5:首碼和與差分
首碼和與差分互為逆運算。
1.首碼和
首先我們先介紹首碼和。先去定義一個數組a,儲存n個數據,然後定義一個數組b,去儲存首碼和。
那麼b[0] = a[0],b[1] = a[0] + a[1],b[2] = a[0] + a[1] + a[2],.......;
以上的b數組就是a的首碼和數組,
首碼和就是將前k個數相加,這個和就是首碼和。
然後我們根據b數組的特點,可以得出以下的遞推公式:
b[i] = b[i-1] + a[i];
有了這個特點之後,我們就可以遞推計算出b數組的全部初始值,代碼如下:
vector<int> s(n + 1);
s[0] = 0;//註意兩個數組的邊界問題
for (int i = 1; i < n + 1; i++)
{
cin >> s[i];
}
vector<int> a;
a.push_back(0);//由於遞推公式中有a[i-1],所以我們的迴圈從i = 1開始,以避免邊界問題,對應的s也從i= 1開始儲存。
for (int i = 1; i <= n; i++)
{
a.push_back(a[i - 1] + s[i]);
}
那麼我們有了初始化之後的首碼和數組之後,就可以很快的計算出一個區間內所有元素的和,
我們輸入所求期間的左邊界l,和右邊界r,那麼這一段區間的和就可以表示為,b[r]-b[l-1];
完整代碼實現如下:
int main()
{
int n, m;//數組長度為n,詢問個數為m
cin >> n >> m;
vector<int> s(n + 1);
s[0] = 0;
for (int i = 1; i < n + 1; i++)
{
cin >> s[i];
}
vector<int> a;
a.push_back(0);
for (int i = 1; i <= n; i++)
{
a.push_back(a[i - 1] + s[i]);
}
while (m--)//m個詢問
{
int l, r;
cin >> l >> r;
cout << a[r] - a[l - 1] << endl;
}
return 0;
}
2.差分
那麼首碼和和差分是分不開的,所以我們下麵去介紹差分。
差分和首碼和是互為逆運算,那麼我們先給出一個首碼和數組a,然後定義一個原數組b;
所以這個a叫做b的首碼和,b叫做a的差分。
那麼我們根據兩者的關係,就可以根據首碼和數組求出原數組,然而我們其實並不需要掌握求原數組的方法,重要的是掌握它的性質。
我們去看一個例題:

1.首先我們將a,b,數組的全部元素全部初始化為0,
2.我們要進行的操作是在l-r之間的每個數+c,其實我們初始時輸入的數組可以看成在i-i之間插入元素a[i],所以將兩種操作合併為一種。
下麵是重點思路:我們將要進行操作的數組看做首碼和數組a,然後假想一個原數組b。
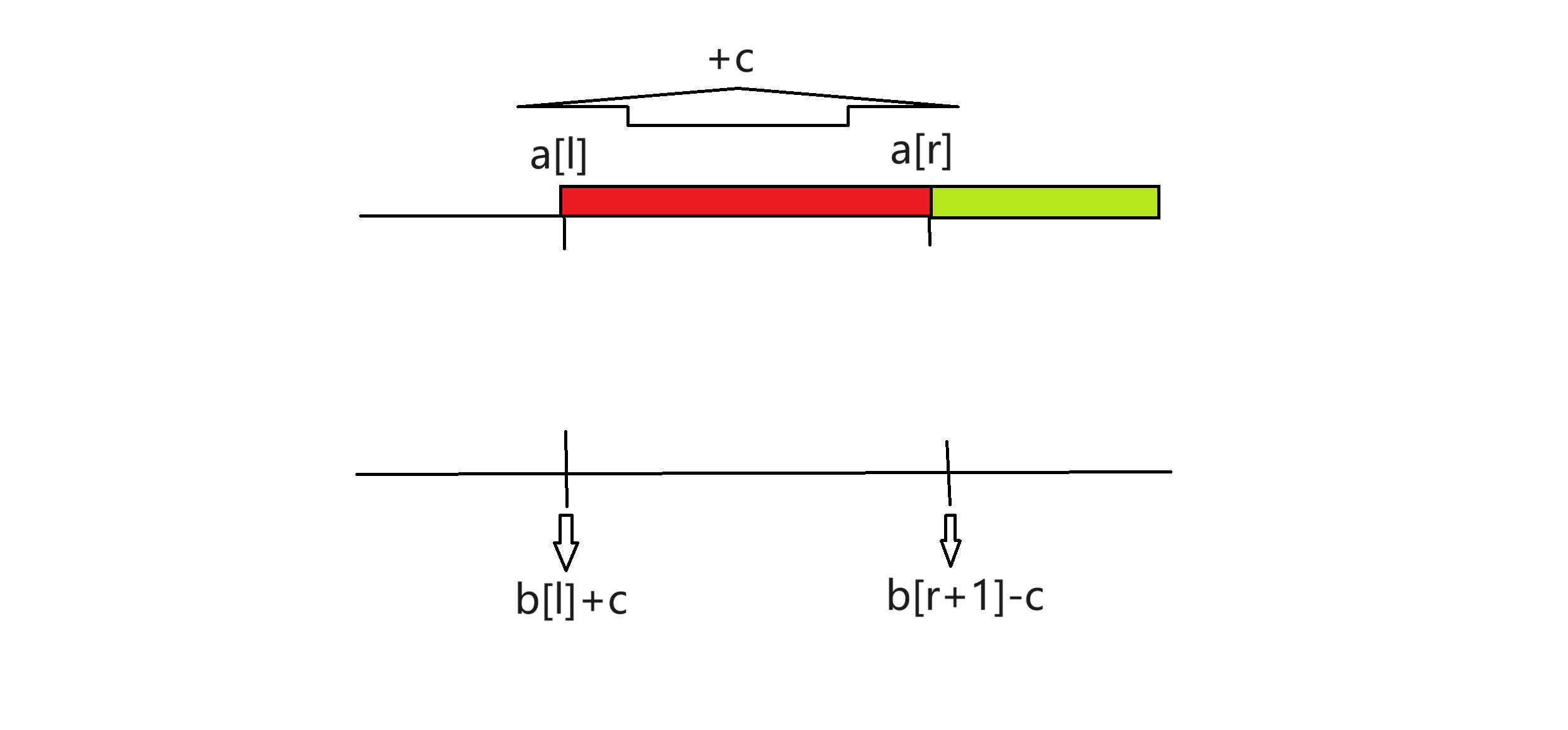
要想在l-r之間的每個數+c,可以將原數組中的b[l]+=c;
那麼在a[l]之後所有的a[]將都加上一個c,(因為圖中紅色部分和綠色部分所有的a[]都含有b[l]這一項);
但我們最終是要在l-r之間的數+c,所以需要打一個補丁(即將a[r+1]-=c,只有綠色部分含有a[r+1],而紅色部分不含有),那麼這樣就使得a[r]之後的所有a[]回歸正常。
總結以上的思路,可以得出核心代碼:
void insert(int l, int r, int x)
{
a[l] += x;
a[r + 1] -= x;
}
完整代碼如下:
const int N = 100010;
int a[N];
void insert(int l, int r, int x)//插入函數
{
a[l] += x;
a[r + 1] -= x;
}
int main()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
{
int x;
cin >> x;
insert(i, i, x);//初始化數組可以看做在i-i之間插入x
}
while (m--)//m組操作
{
int l, r, c;
cin >> l >> r >> c;
insert(l, r, c);
}
for (int i = 1; i <= n; i++)//利用差分求出首碼和數組
{
a[i] += a[i - 1];
}
for (int i = 1; i <= n; i++)
{
cout << a[i] << ' ';
}
return 0;
}
3.二維首碼和
那麼有了以上的基礎,我們將首碼和拓展到2維,求一下二維首碼和;
同樣的道理,我們定義兩個二維數組a,b,a為首碼和數組,b為原數組;
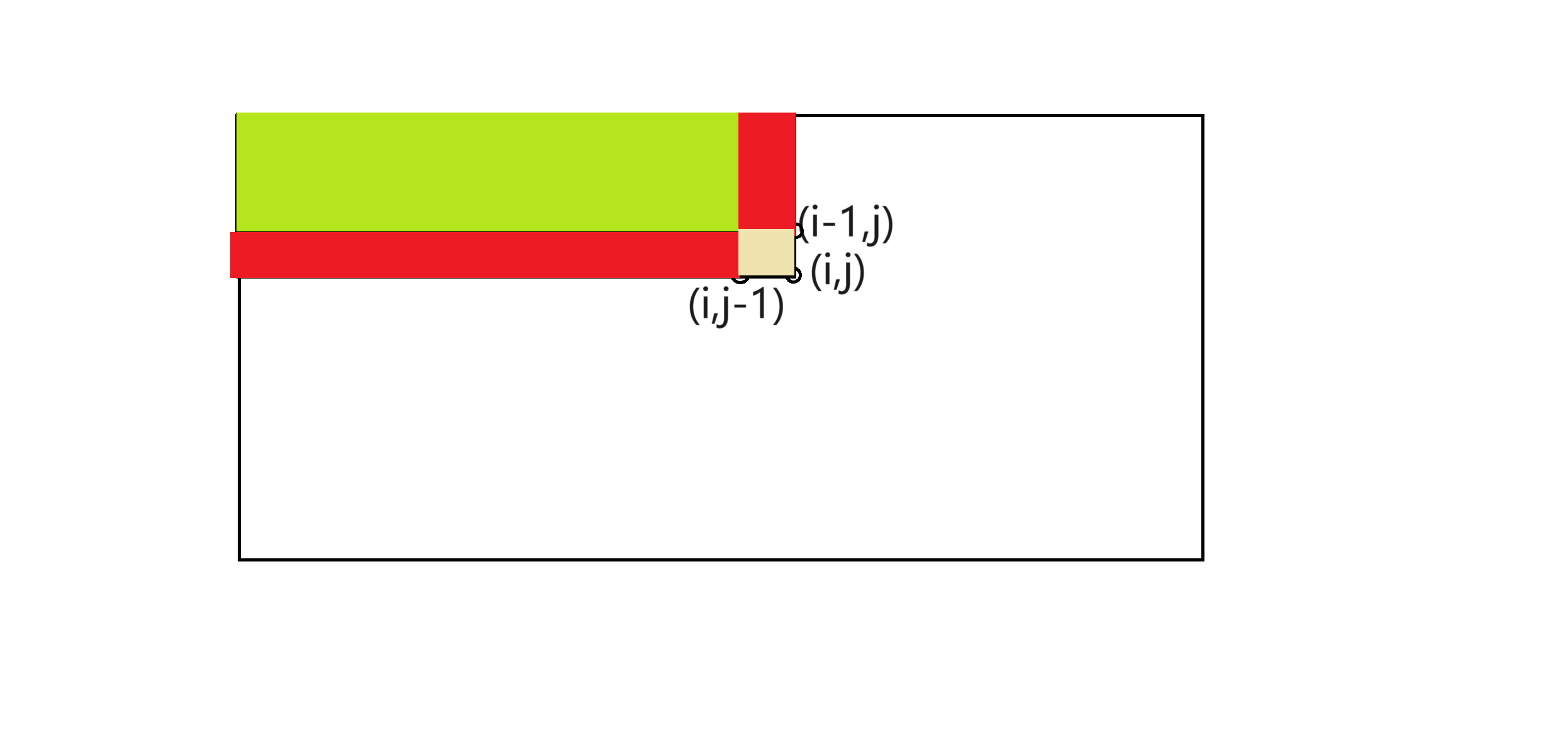
我們要計算首碼和a[i,j];可以看出a[i,j]由兩個紅色部分,一個綠色部分和一個棕色部分組成。
那可以得出表達式:a[i,j] = a[i-1,j]->(一個綠色+一個紅色)+a[i,j-1]->(一個綠色+一個紅色)+b[i,j]->(棕色部分)-a[i-1,j-1]->(減去多餘的綠色部分)
由此得出核心代碼:
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
}
}
那麼我們得到一個已經初始化的首碼和數組,就可以求出圖形中任意一個矩陣中的元素和;
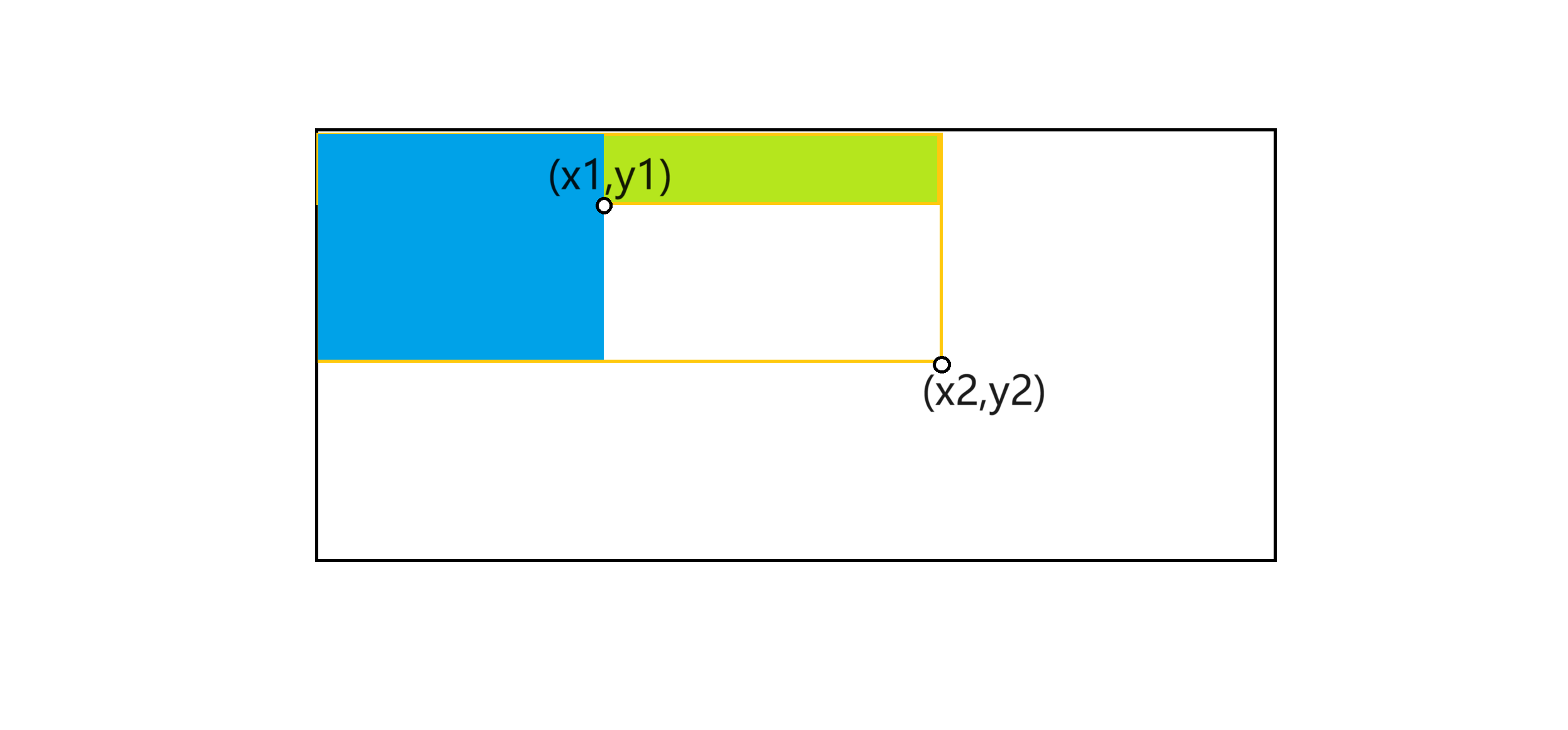
例如上圖,我們要求白色矩陣中所有的元素和,可以用金色邊框內所有的元素減去綠色部分,再減去藍色部分,最後將兩部分重疊的部分加回來,就得到了所求。
代碼如下:
cout << b[x2][y2] - b[x1 - 1][y2] - b[x2][y1 - 1] + b[x1 - 1][y1 - 1]<<endl;
完整代碼:
const int N = 1010;
int n, m, q;
int a[N][N], b[N][N];
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + a[i][j];
}
}
while (q--)
{
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << b[x2][y2] - b[x1 - 1][y2] - b[x2][y1 - 1] + b[x1 - 1][y1 - 1]<<endl;
}
return 0;
}
3.二維差分
同樣的不需要掌握如何求差分,只需要掌握它的性質。
直接看一道題
將數組(x2,y2),(x1,y1)構成的矩陣中的所有元素+c
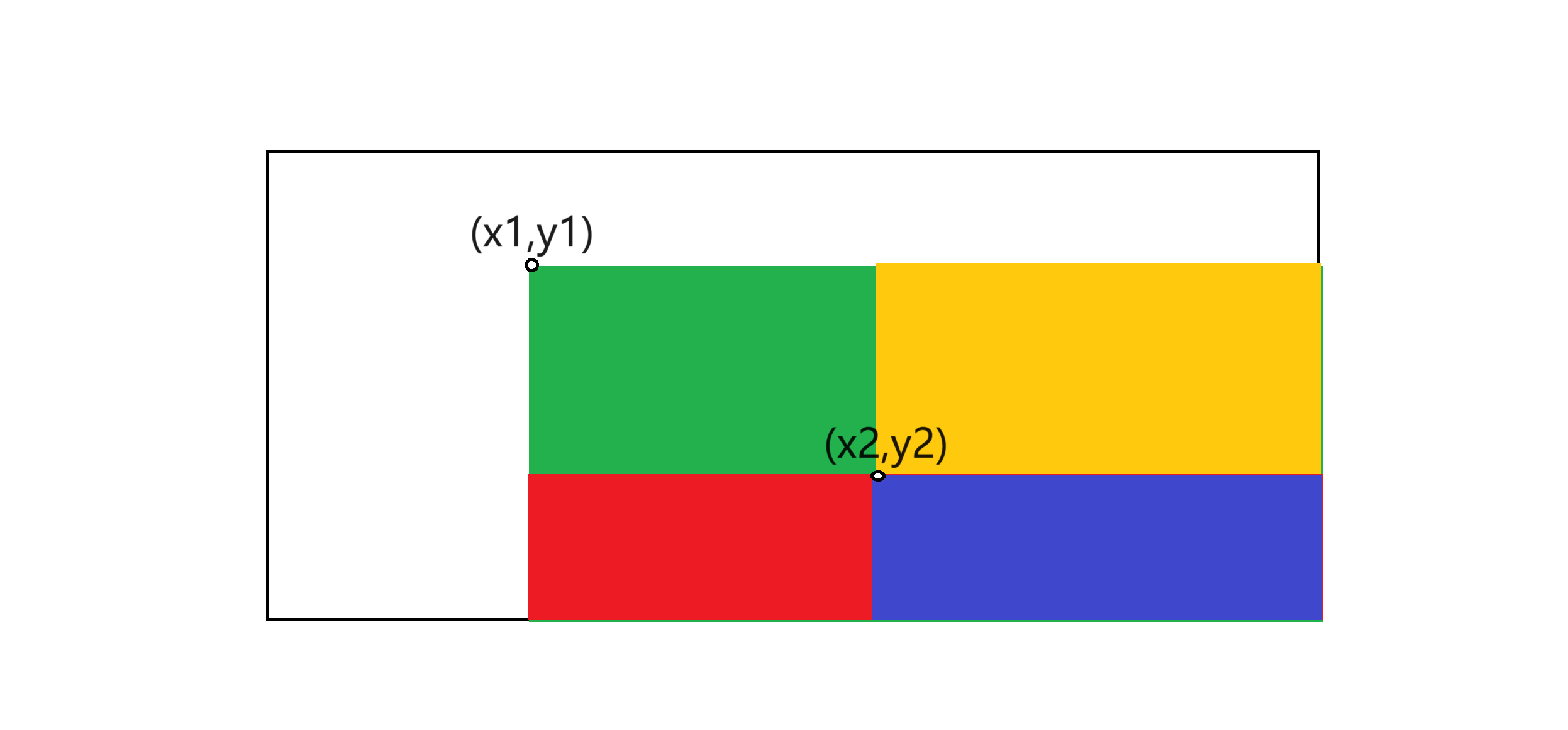
我們還是將要操作的數組看做首碼和數組a,假想一個原數組b。
當我們給b[i,j]+c之後,四個塗色部分將全部+c;
然後我們去打補丁:將b[x1,y2+1]-=c,黃色和藍色部分將-=c;將b[x2+1,y1]-=c,紅色部分和藍色部分將-=c;
然後發現藍色部分多-=c,所以我們讓b[x2+1,y2+1]+=c,那麼藍色部分將+=c;
大功告成,完整代碼如下:
const int N = 1010;
int n, m, q;
int a[N][N];
void insert(int x1, int y1, int x2, int y2,int r)
{
a[x1][y1] += r;
a[x2 + 1][y2 + 1] += r;
a[x1][y2 + 1] -= r;
a[x2 + 1][y1] -= r;
}
int main()
{
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
int x;
cin >> x;
insert(i, j, i, j, x);
}
}
while (q--)
{
int x1, y1, x2, y2,r;
cin >> x1 >> y1 >> x2 >> y2 >> r;
insert(x1, y1, x2, y2, r);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];
cout << a[i][j] << ' ';
}
cout << endl;
}
return 0;
}
以後將不定時更新這個系列,如果對你有幫助的話請點贊支持一下!