作者:凹凸曼 - Barrior 在 Canvas 中對文本填充水平或垂直的線性漸變可以輕易實現,而帶角度的漸變就複雜很多;就好像下麵這樣,假設文本矩形寬為 W, 高為 H, 左上角坐標為 X, Y。 猜想與答案 給出兩個答案: 正確答案是圖二,因為這樣得出來的坐標生成的漸變最緊接文本矩形邊界,它的 ...

作者:凹凸曼 - Barrior
在 Canvas 中對文本填充水平或垂直的線性漸變可以輕易實現,而帶角度的漸變就複雜很多;就好像下麵這樣,假設文本矩形寬為 W, 高為 H, 左上角坐標為 X, Y。

猜想與答案
給出兩個答案:
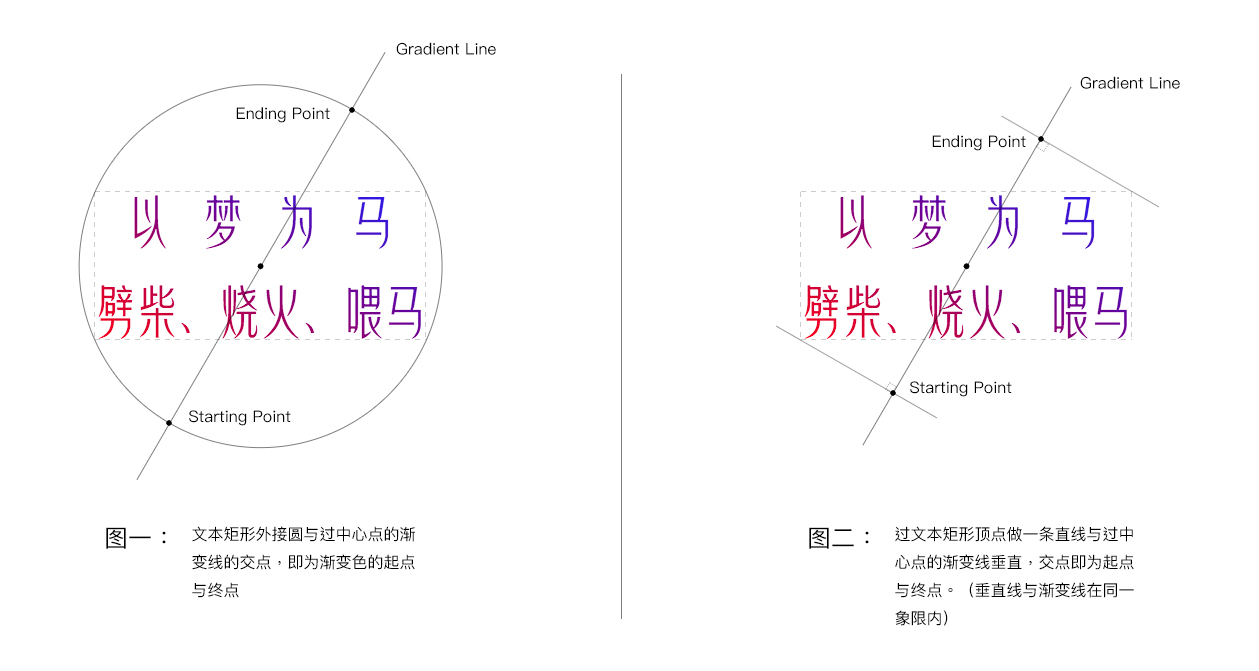
正確答案是圖二,因為這樣得出來的坐標生成的漸變最緊接文本矩形邊界,它的運動軌跡如下動圖:
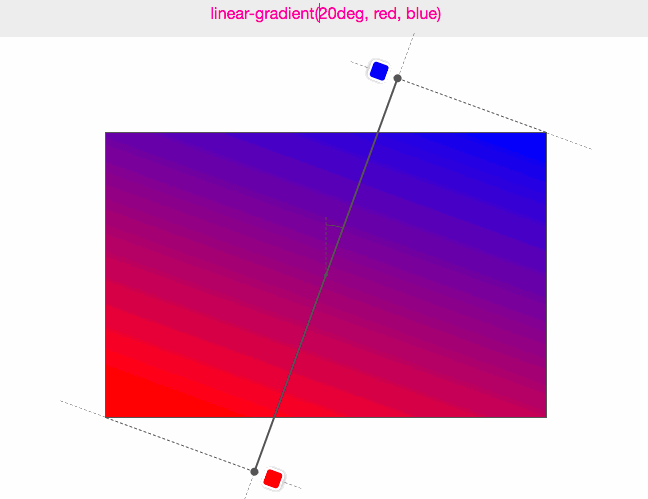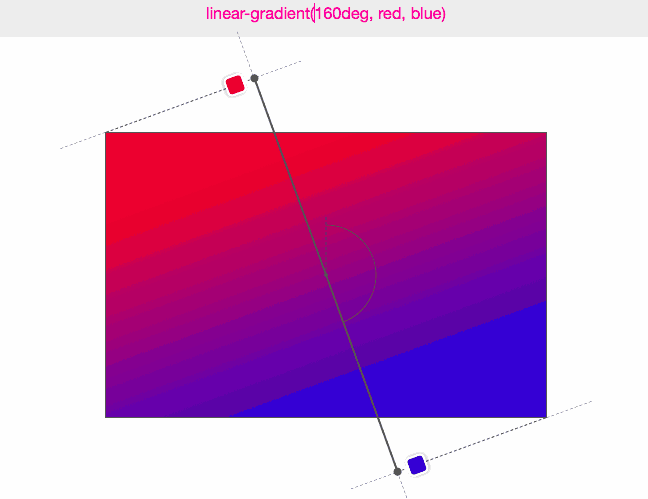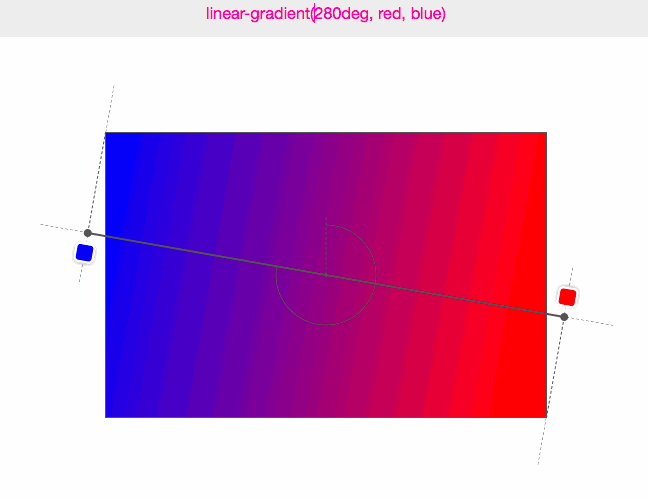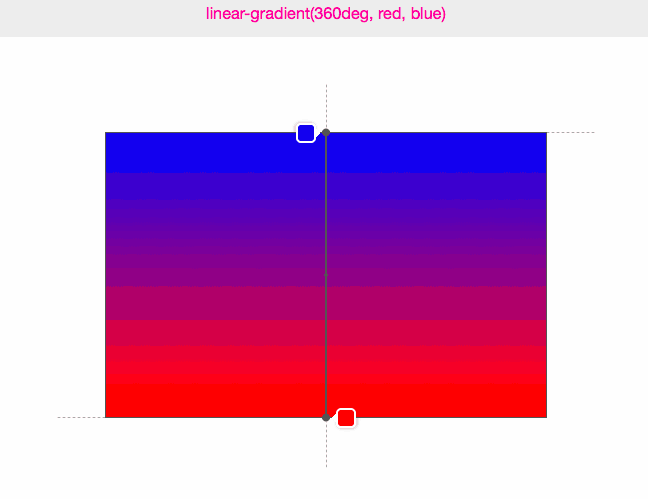
(圖來源:Do you really know CSS linear-gradients)
漸變起點與終點坐標的計算
所以,漸變的起點與終點坐標該怎麼計算呢?答:
- 先求得起點與終點的長度(距離)。
- 根據長度與文本矩形的中心點坐標分別計算出起點與終點坐標。
線性漸變長度的計算 W3C 給出了一個公式(A 表示角度):
gradientLineLength = abs(W * sin(A)) + abs(H * cos(A))
不過,該公式主要應用於 CSS 的線性漸變設置,即以 12 點鐘方向為 0°,順時針旋轉。
而我們需要的是以 3 點鐘方向為 0°,逆時針旋轉,即公式為:
gradientLineLength = abs(W * cos(A)) + abs(H * sin(A))
// 半長:
halfGradientLineLength = (abs(W * cos(A)) + abs(H * sin(A))) / 2
那麼這個公式是怎麼來的呢?以下是筆者的求解:
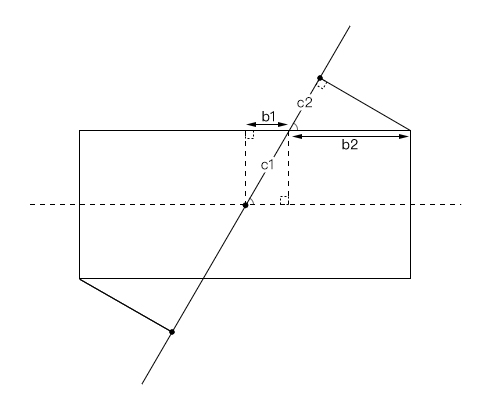
由圖可得以下方程組:
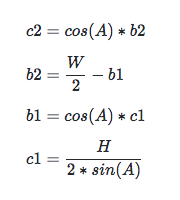
因此可推導出:
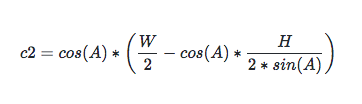
化簡後為:
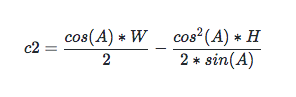
所以 c1 + c2 為:
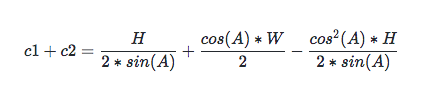
由三角函數平方公式知:cos(A) * cos(A) = 1 - sin(A) * sin(A), 代入 c1 + c2:
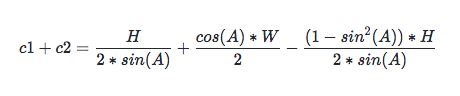
第一步化簡後:
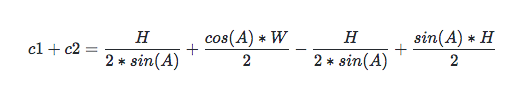
最後的結果就是:
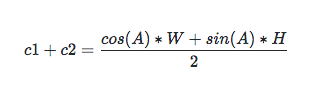
因為 sin, cos 在函數周期記憶體在負值(見下麵角度對應的三角函數周期圖),所以線性漸變的長度需要取絕對值。
至此,我們知道了線性漸變長度,文本矩形的中心點坐標很好算,即:
centerX = X + W / 2
centerY = Y + H / 2
所以,起點與終點的坐標分別為:
startX = centerX - cos(A) * halfGradientLineLength
startY = centerY + sin(A) * halfGradientLineLength
endX = centerX + cos(A) * halfGradientLineLength
endY = centerY - sin(A) * halfGradientLineLength
看看最終效果
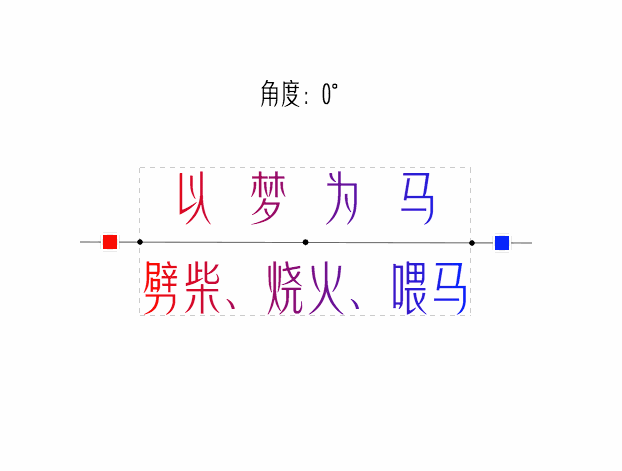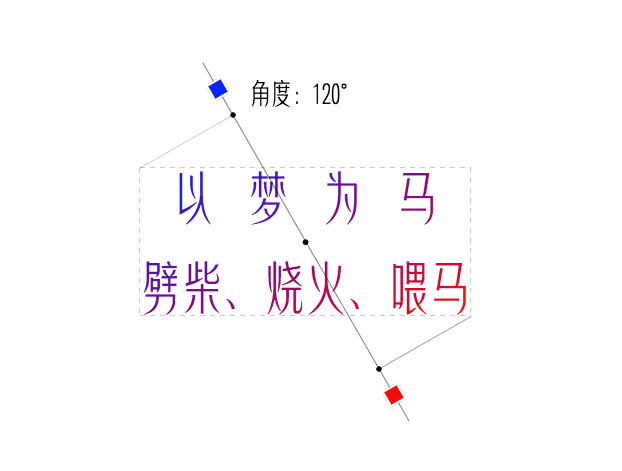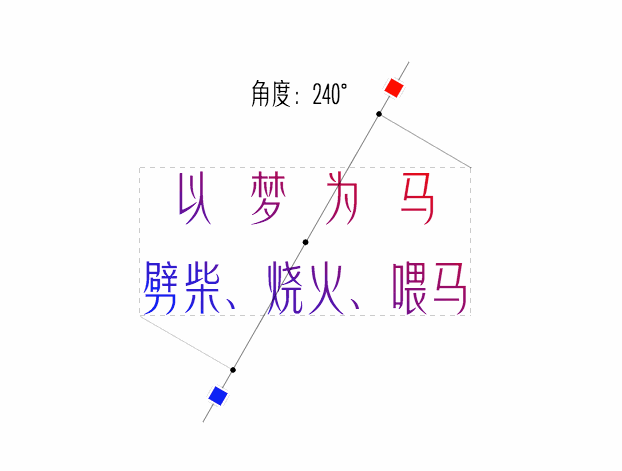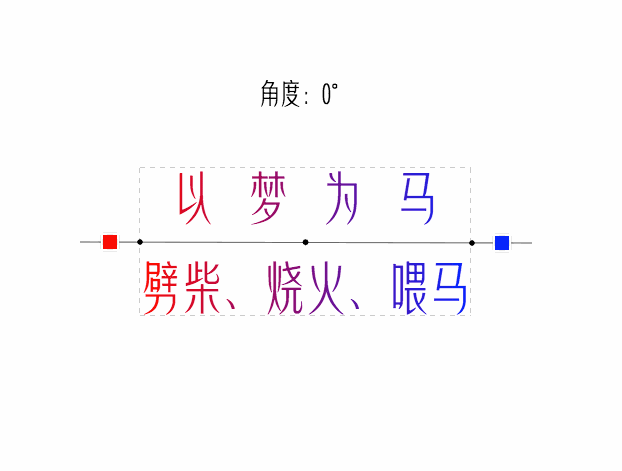
經驗註釋
進行三角函數計算時,應儘量避免先用 tan, 因為 tan 在其周期記憶體在無窮值,需要做特定的條件判斷,而 sin, cos 沒有此類問題,代碼書寫更為簡潔清晰並且不會因疏忽產生錯誤,見下麵三角函數與角度的對應關係周期圖。
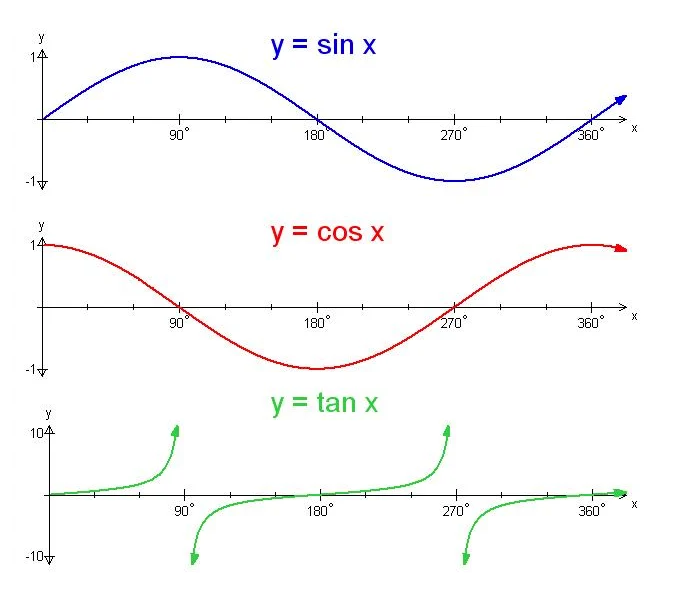
參閱:
Do you really know CSS linear-gradients?
W3C - CSS Images Module Level 3 # linear-gradients
歡迎關註凹凸實驗室博客:aotu.io
或者關註凹凸實驗室公眾號(AOTULabs),不定時推送文章:



