MySQL 樹形索引結構 B樹 B+樹

如何評估適合索引的數據結構

• 索引的本質是一種數據結構
• 記憶體只是臨時存儲，容量有限且容易丟失數據。因此我們需要將數據放在硬碟上。
• 在硬碟上進行查詢時也就產生了硬碟的I/O操作，而硬碟的I/O存取消耗的時間要比讀取記憶體大很多。因此數據查詢的時間主要決定於I/O操作的次數。
• 每訪問一次節點就需要對磁碟進行一次I/O操作。

樹模型

二分查找的時間複雜度是O(log2n)，是一種很高效的查詢方式。在一系類樹種使用二分查找的樹有很多，但並不是所有樹都適合作為索引的結構。

Binary Search Tree 二叉搜索樹（BST）

性質：

• 對任意節點，左子樹不為空則左子樹所有節點小於或等於該節點的值
• 對任意節點，右子樹不為空則右子樹所有節點大於或等於該節點的值

但二叉搜索樹不一定是"平衡的"，它有可能退化成一條鏈表，那麼他的搜索時間就變成了O(n)。

平衡二叉搜索樹（AVL）

為了避免退化成一條鏈表，人們提出了二叉搜索樹，AVL在二叉搜索樹的基礎上增加了約束：

每個節點的左子樹和右子樹的高度差不能超過1

也就是說要求節點的左右子樹仍然為平衡二叉樹。

常見的平衡二叉樹有很多種，包括了AVL樹、紅黑樹、數堆、伸展樹。AVL樹是最早提出來的自AVL樹，當我們提到平衡二叉樹時一般指的就是AVL樹

左右平衡後就使得搜索時間複雜度能穩定在O(log2n)。

但是即便在理論上它的搜索效率高且比較穩定，但是由於“每訪問一次節點就需要進行一次磁碟I/O操作”，在實際情況中只有兩個子節點的情況下，樹的高度依然有可能會很高，比如說現有一個五層共31個節點的樹，那麼我們需要進行5次I/O操作。

B Tree

既然"二叉"結構可能讓樹變得很高，那麼我們自然而然地就明白可以讓子節點數變得更多來減少I/O次數。在文件系統和部分資料庫系統中，B樹就已經得到了實際的應用。

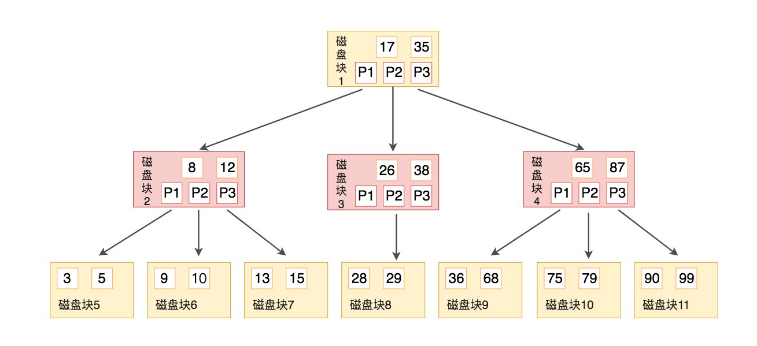
如圖所示，B樹有如下性質

• B樹也是平衡的，每個節點可以有M個子節點，M也稱為B樹的階

• 每個磁碟塊都包含著關鍵字和指針，有k-1個關鍵字，那麼就有k個指針，也就是k個子節點。也就等同於子節點的數量=關鍵字數量+1

• 所有子節點都在同一層，且每個葉子節點沒有子節點，只包含k-1個關鍵字

• 子節點和非子節點都即保存數據記錄又保存索引。

• k-1個關鍵字相當於劃分出了k個範圍，每個範圍對應一個指針。

  例如，有關鍵字Key[1], Key[2], …, Key[k-1]，且關鍵字按照升序排序

  它們劃分出k個範圍對應k個指針，P[1], P[2], …, P[k]

  對應關係就是：P[1]指向關鍵字小於 Key[1]的子樹，P[i]指向關鍵字屬於 (Key[i-1], Key[i]) 的子樹，P[k]指向關鍵字大於 Key[k-1]的子樹

在B樹上的搜索過程就是：

• 要找目標關鍵字n，那麼就從根節點開始，不斷在樹的每一層的每兩個相鄰關鍵字劃定的範圍中尋找包含目標關鍵字的節點，順著索引一直尋找，直到某節點中關鍵字與目標關鍵字相同。

這裡說的關鍵字在實際的資料庫中，其實就是一條實際的數據或者主鍵值，詳細可見此處

MongoDB內部使用的就是B樹

B+ Tree

主流的RDMS大多採用B+樹作為索引結構，包括MySQL的InnoDB引擎（不同存儲引擎的索引的工作方式並不一樣。而即使多個存儲引擎支持同一種類型的索引，其底層的實現也可能不同）

在數據結構性質上與B樹不同的是：

• 有K個孩子就有k個關鍵字。通俗來講，B樹是給每一個範圍一個指針，而B+樹是給每個子節點直接給一個指針。
• 只有葉子節點保存數據記錄，非葉子節點僅用於索引
• 所有關鍵字都在葉子節點中。每層子節點的關鍵字也會保存在下一層子節點中且是子節點關鍵字中最大或最小的那一個，這樣到最後，所有關鍵字都集合在葉子節點中。
• 葉子節點之間會按照關鍵字的大小從小到大，使用雙向鏈表進行串聯。支持了區間查詢。

B+樹 vs B樹

上面說了兩種數據結構性質上的不同，下麵里對比下實際生產中兩種索引結構的區別。

• B+樹查詢效率更穩定。

  B+樹所有的數據記錄都在葉子節點，而B樹的數據記錄可能在葉子節點也可能在非葉子節點，這樣就會導致查詢效率的不穩定。

• B+樹查詢效率更高。

  B+樹的內部節點並沒有指向關鍵字具體信息的指針，因此其內部節點相對B樹更小。那麼盤塊所能容納的關鍵字數量也越多，一次性讀入記憶體的需要查找的關鍵字也就越多，相對IO讀寫次數就降低了。

• B+樹的範圍查詢效率更高。

  B+樹所有葉子節點都通過雙向鏈表進行查詢，方便範圍查詢。

  而B樹因為在非葉子節點中也存有數據記錄，因此範圍查詢時需要通過對樹的中序遍歷才能完成

其他索引見此