JavaScript圖形實例：迭代函數系統生成圖形

来源:https://www.cnblogs.com/cs-whut/archive/2020/07/04/13235992.html
-Advertisement-
Play Games

迭代函數系統（Iterated Function System，IFS）可以用來創建分形圖案，它是分形理論的重要分支，也是分形圖形處理中最富生命力而且最具有廣闊應用前景的領域之一。這一工作最早可以追溯到Hutchinson於1981年對自相似集的研究。美國科學家M.F.Barnsley於1985年發 ...


     迭代函數系統（Iterated Function System，IFS）可以用來創建分形圖案，它是分形理論的重要分支，也是分形圖形處理中最富生命力而且最具有廣闊應用前景的領域之一。這一工作最早可以追溯到Hutchinson於1981年對自相似集的研究。美國科學家M.F.Barnsley於1985年發展了這一分形構型系統，並命名為迭代函數系統（Iterated Function System，IFS），後來又由Stephen Demko等人將其公式化，並引入到圖像合成領域中。IFS將待生成的圖像看做是由許多與整體相似的（自相似）或經過一定變換與整體相似的（自仿射）小塊拼貼而成。

      IFS演算法的基本過程是：

（1）設定一個起始點（x0，y0）及總的迭代步數。

（2）以概率P選取仿射變換W，形式為

         x1=a*x0 + b*y0 + e

         y1=c*x0 + d*y0 + f

（3）以W作用點（x0，y0），得到新坐標（x1，y1）；

（4）在屏幕上坐標（x1，y1）處描點；

（5）令x0=x1，y0=y1，為下一次迭代做準備；

（6）返第（2）步，進行下一次迭代，直到迭代次數大於總步數為止。

      例如，在一個二維平面中，有2種仿射變換函數，可以將一個點映射到另一個位置：

①   x(n+1）= 0.5*x(n)-0.5*y(n)

      y(n+1) = 0.5*x(n)+0.5* y(n)

②   x(n+1) = 0.5 * x(n)+0.5 * y(n)+0.5

      y(n+1) = -0.5 * x(n) + 0.5 * y(n) + 0.5

      給定一個初始點 x(0),y(0)，經過上面的仿射變換函數的映射，便可以得到平面中許多點，這些點構成的圖形便是分形圖案。這個系統就叫做迭代函數系統。

      但是，一共有2個仿射變換函數，每次迭代要使用哪一個呢？因此，需要給每個仿射變換函數規定一個概率，按照概率來進行選擇。

      不妨設2個仿射變換函數的概率均為0.5（各一半），此時演算法步驟為：

      （1）生成一個0~1之間的隨機數r；

      （2）判斷隨機數落入哪一個概率空間，若r<=0.5，則使用仿射變換函數①；否則使用仿射變換函數②；

      （3）根據仿射變換函數計算出新坐標（x1,y1），併在該坐標處畫一個點；

       （4）迴圈執行這一過程，直到達到規定次數。

       按上面的演算法步驟，編寫如下的HTML代碼。

<!DOCTYPE html>

<head>

<title>IFS生成圖形（一）</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var ctx=canvas.getContext('2d');

     ctx.fillStyle="#EEEEFF";

     ctx.fillRect(0,0,600,600);

     ctx.fillStyle="red";

     var x0=0;

     var y0=0;

     for (i=0; i<100000; i++)

     {

         r=Math.random();

         if (r<=0.5)

         {

             x1=0.5*x0-0.5*y0;

             y1=0.5*x0+0.5*y0;

          }

         else

         {

             x1=0.5*x0+0.5*y0+0.5;

             y1=-0.5*x0+0.5*y0+0.5;

         }

         ctx.fillText('.',x1*200+200,y1*200+200);

         x0 = x1;

         y0 = y1;

     }

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">

</canvas>

</body>

</html>

       在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出的C曲線，如圖1所示。

圖1  利用IFS方法生成的C曲線

如果將上面的映射函數改為：

①    x(n+1）= -0.82*x(n)+0.16*y(n)+137

      y(n+1) = -0.16*x(n)+0.81* y(n)+14

②     x(n+1) = 0.44 * x(n)+0.32 * y(n)-3

      y(n+1) = -0.07 * x(n) + 0.61 * y(n) + 70

對應的HTML文件如下：

<!DOCTYPE html>

<head>

<title>IFS生成圖形（一）</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var ctx=canvas.getContext('2d');

     ctx.fillStyle="#EEEEFF";

     ctx.fillRect(0,0,600,600);

     ctx.fillStyle="green";

     var x0=0;

     var y0=0;

     for (i=0; i<100000; i++)

     {

         r=Math.random();

         if (r<=0.5)

         {

             x1=-0.82*x0+0.16*y0+137;

             y1=-0.16*x0+0.81*y0+14;

          }

         else

         {

             x1=0.44*x0+0.32*y0-3;

             y1=-0.07*x0+0.61*y0+70;

         }

         ctx.fillText('.',x1*2+100,y1*2+100);

         x0 = x1;

         y0 = y1;

     }

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">

</canvas>

</body>

</html>

      在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出如圖2所示的樹葉圖案。

 

圖2  利用IFS生成的樹葉

      由圖1和圖2的生成程式可知，IFS方法中仿射變換的形式是相同的，不同的形狀取決於仿射變換的繫數（a,b,c,d,e,f），並且對於一個比較複雜的圖形，可能需要多個不同的仿射變換來實現，並且每一個仿射變換函數被調用的概率P也不一定是等同的。因此，6個仿射變換繫數（a,b,c,d,e,f）和一個概率p便構成了IFS演算法最關鍵的部分——IFS碼。

1．SierPinski三角形

SierPinski三角形採用的仿射變換函數為：

W1： x1=0.5*x0

      y1=0.5*y0

W2： x1=0.5*x0 + 0.5

      y1=0.5*y0

W3： x1=0.5*x0 +0.25

      y1= 0.5*y0 +0.5

      可以讓3個仿射變換函數的調用概率相同或相近，即概率p分別取0.333,0.333,0.334，保證p1+p2+p3=1。

      為程式設計簡潔，將IFS碼中的6個繫數和概率p採用數組保存。編寫如下的HTML代碼（為了後面敘述方便，將這段程式代碼記為“IFS生成圖形（二）”）。

<!DOCTYPE html>

<head>

<title>IFS生成圖形（二）</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var ctx=canvas.getContext('2d');

     ctx.fillStyle="#EEEEFF";

     ctx.fillRect(0,0,500,500);

     ctx.fillStyle="red";

     var a=[0.5,0.5,0.5];

     var b=[0,0,0];

     var c=[0,0,0];

     var d=[0.5,0.5,0.5];

     var e=[0,0.5,0.25];

     var f=[0,0,0.5];

     var p=[0.333,0.333,0.334];

     var x0=0;

     var y0=0;

     for (i=0; i<10000; i++)

     {

         r=Math.random();

         if (r<=p[0])

             index=0;

         else if (r<=p[0]+p[1])

             index=1;

         else

             index=2;

         x1=a[index]*x0+b[index]*y0+e[index];

         y1=c[index]*x0+d[index]*y0+f[index];

         ctx.fillText('.',x1*300+100,400-y1*300);

         x0 = x1;

         y0 = y1;

     }

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="500" height="500" style="border:3px double #996633;">

</canvas>

</body>

</html>

      在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出的SierPinski三角形，如圖3所示。

 

圖3  SierPinski三角形

      前面介紹過，IFS的關鍵部分是IFS碼，不同的IFS碼生成不同的圖形。

      例如，“IFS生成圖形（二）”程式中的IFS碼定義改寫為：

     var a=[0.5,0.5,0.5];

     var b=[0,0,0];

     var c=[0,0,0];

     var d=[0.5,0.5,0.5];

     var e=[0,0.5,0.5];

     var f=[0,0.5,0];

     var p=[0.333,0.333,0.334];

      則在瀏覽器視窗中繪製出如圖4所示的直角SierPinski三角形。

圖4  直角SierPinski三角形

2．蕨類植物

      可以使用4個仿射變換函數來生成蕨類植物的圖案，編寫如下的HTML代碼（為了後面敘述方便，將這段程式代碼記為“IFS生成圖形（三）”）。

<!DOCTYPE html>

<head>

<title>IFS生成圖形（三）</title>

<script type="text/javascript">

  function draw(id)

  {

     var canvas=document.getElementById(id);

     if (canvas==null)

        return false;

     var ctx=canvas.getContext('2d');

     ctx.fillStyle="#EEEEFF";

     ctx.fillRect(0,0,600,600);

     ctx.fillStyle="green";

     var a=[0,0.2,-0.15,0.85];

     var b=[0,-0.26,0.28,0.04];

     var c=[0,0.23,0.26,-0.04];

     var d=[0.16,0.22,0.24,0.85];

     var e=[0,0,0,0];

     var f=[0,1.6,0.44,1.6];

     var p=[0.01,0.07,0.07,0.85];

     var x0=0;

     var y0=0;

     for (i=0; i<100000; i++)

     {

         r=Math.random();

         if (r<=p[0])

             index=0;

         else if (r<=p[0]+p[1])

             index=1;

         else if (r<p[0]+p[1]+p[2])

             index=2;

         else

             index=3;

         x1=a[index]*x0+b[index]*y0+e[index];

         y1=c[index]*x0+d[index]*y0+f[index];

         ctx.fillText('.',x1*50+300,550-y1*50);

         x0 = x1;

         y0 = y1;

     }

   }

</script>

</head>

<body onload="draw('myCanvas');">

<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">

</canvas>

</body>

</html>

      在瀏覽器中打開包含這段HTML代碼的html文件，可以看到在瀏覽器視窗中繪製出的蕨類植物圖案，如圖5所示。

圖5  IFS方法生成的蕨類植物（一）

     將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[0,0.21,-0.2,0.85];

     var b=[0,-0.25,0.26,0.1];

     var c=[0,0.25,0.23,-0.05];

     var d=[0.16,0.21,0.22,0.85];

     var e=[0,0,0,0];

     var f=[0,0.44,0,0.6];

     var p=[0.01,0.07,0.07,0.85];

      可在瀏覽器視窗中繪製出如圖6所示的蕨類植物。

圖6  IFS方法生成的蕨類植物（二）

3．樹形圖案

      將“IFS生成圖形（二）”程式中的IFS碼定義改寫為：

     var a=[0.387,0.441,-0.468];

     var b=[0.430,-0.091,0.020];

     var c=[0.430,-0.009,-0.113];

     var d=[-0.387,-0.322,0.015];

     var e=[0.2560,0.4219,0.4];

     var f=[0.5220,0.5059,0.4];

     var p=[0.333,0.333,0.334];

      可在瀏覽器視窗中繪製出如圖7所示的嫩枝圖案。

 

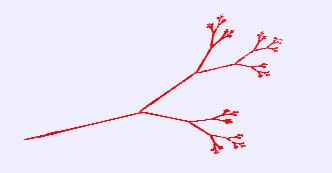
圖7  嫩枝

 

 將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[0.01,-0.01,0.42,0.42];

     var b=[0,0,-0.42,0.42];

     var c=[0,0,0.42,-0.42];

     var d=[0.45,-0.45,0.42,0.42];

     var e=[0,0,0,0];

     var f=[0,0.4,0.4,0.4];

     var p=[0.05,0.15,0.4,0.4];

可在瀏覽器視窗中繪製出如圖8所示的樹形圖案。

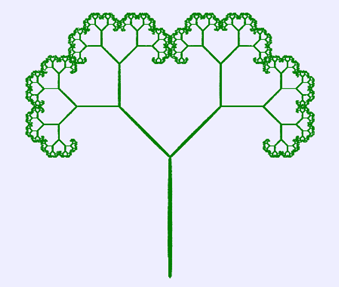
圖8 樹形圖案（一）

 

      將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[0,0.42,0.42,0.1];

     var b=[0,-0.42,0.42,0];

     var c=[0,0.42,-0.42,0];

     var d=[0.5,0.42,0.42,0.4];

     var e=[0,0,0,0];

     var f=[0,0.4,0.4,0.4];

     var p=[0.05,0.4,0.4,0.15];

      可在瀏覽器視窗中繪製出如圖9所示的樹形圖案，並好像還有蟬在樹上。

 

圖9  樹上的蟬

    將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[0.03,-0.03,0.56,0.56];

     var b=[0,0,-0.56,0.56];

     var c=[0,0,0.56,-0.56];

     var d=[0.45,-0.45,0.56,0.56];

     var e=[0,0,0,0];

     var f=[0,0.4,0.4,0.4];

     var p=[0.05,0.15,0.4,0.4];

      可在瀏覽器視窗中繪製出如圖10所示的樹形圖案。

圖10  樹形圖案（二） 

    將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[-0.04,-0.65,0.41,0.52];

     var b=[0,0,0.46,-0.35];

     var c=[-0.19,0,-0.39,0.25];

     var d=[-0.47,0.36,0.61,0.74];

     var e=[-0.12,0.06,0.46,-0.48];

     var f=[0.3,1.56,0.4,0.38];

     var p=[0.25,0.25,0.25,0.25];

      可在瀏覽器視窗中繪製出如圖11所示的樹形圖案。

圖11  樹形圖案（三） 

       還可以使用5個仿射變換函數來生成樹形圖案，參照“IFS生成圖形（二）”和“IFS生成圖形（三）”，適當添加一個條件選擇語句即可，這裡不再給出源程式。

      5個仿射變換函數的IFS碼定義如下：

     var a=[0.195,0.462,-0.058,-0.035,-0.637];

     var b=[-0.488,0.414,-0.07,0.07,0];

     var c=[0.344,-0.252,0.453,-0.469,0];

     var d=[0.433,0.361,-0.111,-0.022,0.501];

     var e=[0.4431,0.2511,0.5976,0.4884,0.8562];

     var f=[0.2452,0.5692,0.0969,0.5069,0.2513];

     var p=[0.25,0.25,0.25,0.2,0.05];

      可在瀏覽器視窗中繪製出如圖12所示的樹形圖案。

圖12  樹形圖案（四）

4．雪花

    將“IFS生成圖形（三）”程式中的IFS碼定義改寫為：

     var a=[0.255,0.255,0.255,0.37];

     var b=[0,0,0,-0.642];

     var c=[0,0,0,0.642];

     var d=[0.255,0.255,0.255,0.37];

     var e=[0.3726,0.1146,0.6306,0.6356];

     var f=[0.6714,0.2232,0.2232,-0.0061];

     var p=[0.2,0.2,0.2,0.4];

       可在瀏覽器視窗中繪製出如圖13所示的雪花圖案。

圖13  雪花圖案（一）

       還可以使用5個仿射變換函數來生成雪花圖案，IFS碼定義如下：

     var a=[0.382,0.382,0.382,0.382,0.382];

     var b=[0,0,0,0,0];

     var c=[0,0,0,0,0];

     var d=[0.382,0.382,0.382,0.382,0.382];

     var e=[0.3072,0.6033,0.0139,0.1253,0.492];

     var f=[0.619,0.4044,0.4044,0.0595,0.0595];

     var p=[0.2,0.2,0.2,0.2,0.2];

       可在瀏覽器視窗中繪製出如圖14所示的雪花圖案。

 

圖14  雪花圖案（二） 


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • Shell：結構化語句
    ver: 1.0 博客：https://www.cnblogs.com/Rohn 本文介紹了Shell常用的結構化語句。 數組 數組(Array)是若幹數據的集合，其中的每一份數據都稱為元素(Element)。 Bash只支持一維數組(不支持多維數組)，初始化時不需要定義數組大小，理論上可以存放無限 ...
  • hbase2.1.9 centos7 完全分散式 搭建隨記
    hbase2.1.9 centos7 完全分散式 搭建隨記 這裡是當初在三個ECS節點上搭建hadoop+zookeeper+hbase+solr的主要步驟，文章內容未經過潤色，請參考的同學搭配其他博客一同使用，並記得根據實際情況調整相關參數 1. 指定位置解壓 2. vi /etc/profile ...
  • zookeeper3.5.5 centos7 完全分散式 搭建隨記
    zookeeper3.5.5 centos7 完全分散式 搭建隨記 這裡是當初在三個ECS節點上搭建hadoop+zookeeper+hbase+solr的主要步驟，文章內容未經過潤色，請參考的同學搭配其他博客一同使用，並記得根據實際情況調整相關參數 0.prepare 準備奇數台已經配置好jdk的 ...
  • Hadoop2.7.7 centos7 完全分散式 配置與問題隨記
    Hadoop2.7.7 centos7 完全分散式 配置與問題隨記 這裡是當初在三個ECS節點上搭建hadoop+zookeeper+hbase+solr的主要步驟，文章內容未經過潤色，請參考的同學搭配其他博客一同使用，並記得根據實際情況調整相關參數。 0.prepare jdk，推薦1.8 關閉防 ...
  • 資料庫分庫分表之後，你是如何解決事務問題？
    我們需要接受失望，因為它是有限的；我們不會失去希望，因為它是無窮的。 一、概述 隨著時間和業務的發展，資料庫中表的數據量會越來越大，相應地，數據操作，增刪改查的開銷也會越來越大。因此，把其中一些大表進行拆分到多個資料庫中的多張表中。 本篇文章是基於非事務消息的非同步確保的方式來完成分庫分表中的事務問題 ...
  • MySQL索引 索引分類 最左首碼原則 覆蓋索引 索引下推 聯合索引順序
    MySQL索引 索引分類 最左首碼原則 覆蓋索引 索引下推 聯合索引順序 What's Index ? 索引就是幫助RDBMS高效獲取數據的數據結構。 索引可以讓我們避免一行一行進行全表掃描。它的價值就是可以幫助你對數據進行快速定位。 索引分類 按照功能邏輯來分 普通索引 INDEX(col_nam ...
  • Flutter第一個應用--踩坑之路
    Flutter第一個應用--踩坑之路 安裝 參照官網教程（這裡)下載解壓，以及設置環境變數即可。 如果你是中國用戶（當然了，我們都是），參考這篇文章Using Flutter in China,設置一下中國的鏡像。 比如我用的是zsh,那我的設置如下： export PUB_HOSTED_URL=h ...
  • JS數據類型判斷的幾種方法
    JS數據類型判斷 JavaScript 中常見數據類型有Number、String、Boolean、Object、Array、Json、Function、Date、RegExp、Error、undefined、Null等十幾種。ES6還有新增的數據類型有Symbol、Set、Map等。在實際應用中， ...
一周排行
    -Advertisement-
    Play Games
  • UOS 開啟 VisualStudio 遠程調試 .NET 應用之旅
    前言 在我們開發過程中基本上不可或缺的用到一些敏感機密數據，比如SQL伺服器的連接串或者是OAuth2的Secret等，這些敏感數據在代碼中是不太安全的，我們不應該在源代碼中存儲密碼和其他的敏感數據，一種推薦的方式是通過Asp.Net Core的機密管理器。 機密管理器 在 ASP.NET Core ...
  • C# - 能否讓 SortedSet.RemoveWhere 內傳入的委托非同步執行
    新改進提供的Taurus Rpc 功能，可以簡化微服務間的調用，同時可以不用再手動輸出模塊名稱，或調用路徑，包括負載均衡，這一切，由框架實現並提供了。新的Taurus Rpc 功能，將使得服務間的調用，更加輕鬆、簡約、高效。 ...
  • 順序棧的介面程式
    順序棧的介面程式 目錄順序棧的介面程式頭文件創建順序棧入棧出棧利用棧將10進位轉16進位數驗證 頭文件 #include <stdio.h> #include <stdbool.h> #include <stdlib.h> 創建順序棧 // 指的是順序棧中的元素的數據類型，用戶可以根據需要進行修改 ...
  • mORMot2 獲取數據集1
    前言 整理這個官方翻譯的系列，原因是網上大部分的 tomcat 版本比較舊，此版本為 v11 最新的版本。 開源項目 從零手寫實現 tomcat minicat 別稱【嗅虎】心有猛虎，輕嗅薔薇。 系列文章 web server apache tomcat11-01-官方文檔入門介紹 web serv ...
  • 萬字長文總結與剖析C語言關鍵字 -- <<C語言深度解剖>>
    C總結與剖析:關鍵字篇 -- <<C語言深度解剖>> 目錄C總結與剖析:關鍵字篇 -- <<C語言深度解剖>>程式的本質:二進位文件變數1.變數:記憶體上的某個位置開闢的空間2.變數的初始化3.為什麼要有變數4.局部變數與全局變數5.變數的大小由類型決定6.任何一個變數,記憶體賦值都是從低地址開始往高地 ...
  • 【Flink入門修煉】2-3 Flink Checkpoint 原理機制
    如果讓你來做一個有狀態流式應用的故障恢復，你會如何來做呢？ 單機和多機會遇到什麼不同的問題？ Flink Checkpoint 是做什麼用的？原理是什麼？ ...
  • C++ 多級繼承與多重繼承：代碼組織與靈活性的平衡
    C++ 多級繼承 多級繼承是一種面向對象編程（OOP）特性，允許一個類從多個基類繼承屬性和方法。它使代碼更易於組織和維護，並促進代碼重用。 多級繼承的語法 在 C++ 中，使用 : 符號來指定繼承關係。多級繼承的語法如下： class DerivedClass : public BaseClass1 ...
  • 圖文結合手把手教你創建SpringCloud項目
    前言 什麼是SpringCloud？ Spring Cloud 是一系列框架的有序集合，它利用 Spring Boot 的開發便利性簡化了分散式系統的開發，比如服務註冊、服務發現、網關、路由、鏈路追蹤等。Spring Cloud 並不是重覆造輪子，而是將市面上開發得比較好的模塊集成進去，進行封裝，從 ...
  • 類模板的常見用法
    class_template 類模板和函數模板的定義和使用類似，我們已經進行了介紹。有時，有兩個或多個類，其功能是相同的，僅僅是數據類型不同。類模板用於實現類所需數據的類型參數化 template<class NameType, class AgeType> class Person { publi ...
  • system-v IPC共用記憶體通信
    目錄system v IPC簡介共用記憶體需要用到的函數介面shmget函數--獲取對象IDshmat函數--獲得映射空間shmctl函數--釋放資源共用記憶體實現思路註意 system v IPC簡介 消息隊列、共用記憶體和信號量統稱為system v IPC(進程間通信機制)，V是羅馬數字5，是UNI ...
所有分類