快速排序的離散數學分析

QUICKSORT(A,p,r)
1  if p<r
2     then q = PARTITION(A,p,r)
3         QUICKSORT(A,p,q-1)
4         QUICKSORT(A,q+1,r)

RANDOMIZED-PARTITION(A,p,r)
1  i=RANDOM(p,r)
2  exchange A[r]<->A[i]
3  return PARTITION(A,p,r)

PARTITION(A,p,r)
1  x=A[r]
2  i=p-1
3  for j=p to r-1
4     do if A[j]<=x
5         then i=i+1
6            exchange A[i]<->A[j]
7  exchange A[i+1]<->A[r]
8  return i+1

這裡為了效率更高效，把切分值改成隨機化，演算法原碼請參考 演算法-5.快速排序

1.最壞情況分析

如果快速排序中每一層遞歸上所做的都是最壞情況劃分，則運行時間為Θ(n²)。從直覺上看，這就是最壞情況運行時間。下麵來證明。

利用代換法，可以證明快速排序的運行時間為O(n²)。設T(n)是過程QUICKSORT作用於規模為n的輸入上的最壞情況時間，則有：

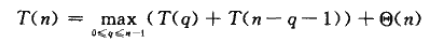　　（遞歸式1）

其中參數q由0變到n-1，這是因為過程PARTITION產生兩個子問題，總的大小為n-1.我們猜測T(n)<=cn²成立，c為某個常數。將此式代入遞歸式1，得：

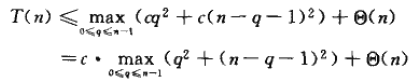
表達式q²+(n-q-1)²在參數的取值區間0<=q<=n-1的某個端點上取得最大值，因為該式關於q的二階導數是正的（所以原表達式是凹函數，並且當q=(n-1)/2時為最小值）。這樣，就有界

對T(n)就有：

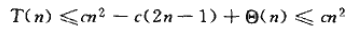
因為我們可以選擇足夠大的常數c，使得項c(2n-1)能支配Θ(n)。於是，快速排序的（最壞情況）運行時間為Θ(n²)。

2.期望的運行時間（即平均運行時間）

設當QUICKSORT在一個包含n個元素的數組上運行時，PARTITION在第4行中所做比較的總次數為X。那麼，QUICKSORT的運行時間為O(n+X)。證明：

根據對PARTITION的調用共有n次。每一次調用都需做固定量的工作，再執行若幹次for迴圈。在for迴圈的每一輪迭代中，都要執行第4行。

我們的目標是計算出X，即在對PARTITION的所有調用中，所執行的總的比較次數。我們並不打算分析在每一次PARTITION調用中做了多少次比較，而是希望導出關於總的比較次數的一個界。為了達到這一目的，我們必須瞭解演算法在何時要對數組中的兩個元素進行比較，何時不進行比較。為了便於分析，我們將數組A的各個元素重新命名為z₁，z₂，...，z_n，其中z_i 是數組A中第i個最小的元素。此外，我們還定義Z_ij={z_i， z_i+1， ... ，z_j}為z_i 與z_j 之間（包含這兩個元素）的元素集合。

那麼，演算法何時會比較z_i 與z_j 呢？為了回答這個問題，我們首先觀察到每一對元素至多比較一次。這是為什麼呢？因為各個元素僅與主元元素進行比較，並且，在某一次PARTITION調用結束之後，該次調用中所用到的主元元素就再也不會與任何其他元素進行比較了。

我們的分析要用到指示器隨機變數，我們定義

我們要考慮的是在演算法的執行過程中，是否有任何的比較發生，而不是在迴圈的一次迭代或對PARTITION的一次調用中是否有比較發生。因為每一對元素至多被比較一次，因而，我們可以很容易地刻划算法所執行的總的比較次數：

對上式兩邊取期望值，再利用期望值的線性特性和引理1，可以得到：

在上式中，Pr{z_i 與z_j 進行比較}還有待於進一步計算。

一般而言，一旦一個滿足z_i<x<z_j 的主元x被選擇後，我們知道，z_i 與z_j 以後是再也不可能進行比較了。另一方面，如果z_i 在Z_ij 中的所有其他元素之前被選為主元，那麼z_i 就將與Z_ij 中的除了它自己以外的所有元素進行比較。類似地，如果z_i 在Z_ij 中其他元素之前被選為主元，那麼z_j 將與Z_ij 中除自身以外的每項進行比較。由此我們知道，z_i 會與z_j 進行比較，當且僅當Z_ij中將被選作主元的第一個元素是z_i 或z_j。

我們現在來計算這一事件發生的概率。在Z_ij中的某一元素被選為主元之前，集合Z_ij 整個都是在同一划分中的。於是，Z_ij中的任何元素都會等可能地被首先選為主元。因為集合Z_ij中共有j-i+1個元素，所以，任何元素被首先選為主元的概率是1/(j-i+1)。於是，我們有：

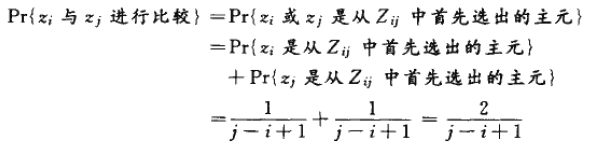
上式中的第二行成立是因為其中涉及的兩個事件是互斥的。將等式綜合起來，有：

在求這個和式時，可以將變數作個變換（k=j-i），並利用等式1中給出的有關調和級數的界：

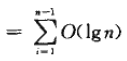
於是，我們可以得出結論，即利用RANDOMIZED-PARTITION，快速排序演算法期望的運行時間為O(nlgn)。

引理1：給定樣本空間S和S中的事件A，令X_A=I{A}，則E[X_A]=Pr{A}

等式1：