ARMR模型簡單實踐（1）

1.概念簡述

（1）AR模型

在ARMA/ARIMA這樣的自回歸模型中，模型對時間序列數據的平穩是有要求的，因此，需要對數據或者數據的n階差分進行平穩檢驗，而一種常見的方法就是ADF檢驗，即單位根檢驗。

平穩隨機過程

在數學中，平穩隨機過程（Stationary random process）或者嚴平穩隨機過程（Strictly-sense stationary random process），又稱狹義平穩過程，是在固定時間和位置的概率分佈與所有時間和位置的概率分佈相同的隨機過程：即隨機過程的統計特性不隨時間的推移而變化。這樣，數學期望和方差這些參數也不隨時間和位置變化。

平穩在理論上有嚴平穩和寬平穩兩種，在實際應用上寬平穩使用較多。寬平穩的數學定義為：

對於時間序列 ytyt，若對任意的t,k,mt,k,m，滿足：

$$E(y_t) = E(y_{t+m})\\

cov(y_t, y_{t+k}) = cov(y_{t+k}, y_{t+k+m})$$

則稱時間序列 ytyt 是寬平穩的。

平穩是自回歸模型ARMA的必要條件，因此對於時間序列，首先要保證應用自回歸的n階差分序列是平穩的。

def draw_rend(timerise, size):
    # print(timerise)
    f = plt.figure(facecolor='white')  # 畫圖板
    rol_mean = timerise.rolling(window=size).mean()  # 對數據時間移動平均計算
    rol_std = timerise.rolling(window=size).std()
    # rol_ = timerise.rolling(window=size).std()
    timerise.plot(color='c', label='原數據')
    rol_std.plot(color='red', label="移動方差")
    rol_mean.plot(color='blue', label="移動平均值")
    plt.title("願數據，均值,方差")
    plt.legend(loc='best')
    plt.show()

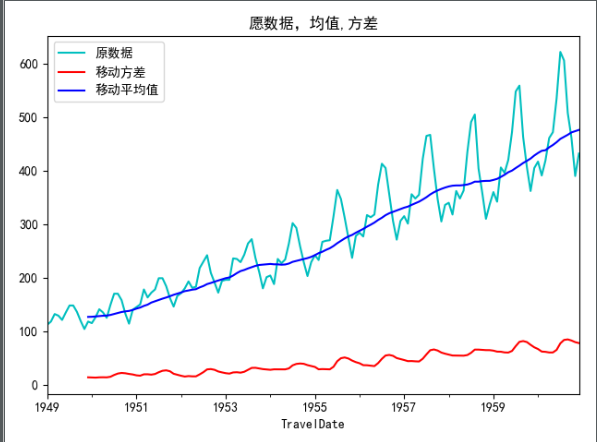
def teststationayity(ts):
    dftest = adfuller(ts)  # 實例化檢驗得到數值源
    # print(dftest)
    dfoutput = pd.Series(dftest[0:4], index=['Test Statistic', 'p_value', '#Lags Used',
                                             'Number of Observation Uesd'])
    # print(dfoutput)
    #n階差分
    # _data=pd.Series(ts)
    # data=_data.diff(1)[1:]
    # # print(data)
    # data.plot()
    # plt.show()
    # plt.savefig('./diff_1.svg')

    for key, value in dftest[4].items():
        dfoutput['Critical Value({})'.format(key)] = value
    return dfoutput

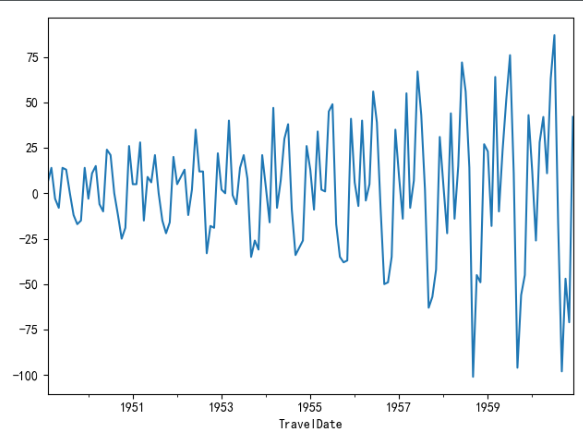
一階差分後很明顯是不平穩的波動

（差分：差分的目的主要是消除一些波動 使數據趨於平穩
你說的沒錯 一階差分後的確就是增量 這還比較好解釋  而有時候一階差分都未必能達到平穩，此時還要做二階差分 這個就很難解釋意義了
所以對於多變數的時序 一般如果不平穩 我們會選擇檢驗他們是否同階單整然後在同階單整的情況下做協整分析  只要有協整關係 就可以用原始數據來建模  我的理解就是放寬了平穩的要求 畢竟經濟數據要平穩很多時候是難以達到的）

3.光看圖沒底兒，故而再瞅瞅單位根檢驗（adf）：

（1）概念簡述：

ADF檢驗
在使用很多時間序列模型的時候，如 ARMA、ARIMA，都會要求時間序列是平穩的，所以一般在研究一段時間序列的時候，第一步都需要進行平穩性檢驗，除了用肉眼檢測的方法，另外比較常用的嚴格的統計檢驗方法就是ADF檢驗，也叫做單位根檢驗。

ADF檢驗全稱是 Augmented Dickey-Fuller test，顧名思義，ADF是 Dickey-Fuller檢驗的增廣形式。DF檢驗只能應用於一階情況，當序列存在高階的滯後相關時，可以使用ADF檢驗，所以說ADF是對DF檢驗的擴展。

單位根（unit root）
在做ADF檢驗，也就是單位根檢驗時，需要先明白一個概念，也就是要檢驗的對象——單位根。

當一個自回歸過程中： ，如果滯後項繫數b為1，就稱為單位根。當單位根存在時，自變數和因變數之間的關係具有欺騙性，因為殘差序列的任何誤差都不會隨著樣本量（即時期數）增大而衰減，也就是說模型中的殘差的影響是永久的。這種回歸又稱作偽回歸。如果單位根存在，這個過程就是一個隨機漫步（random walk）。

ADF檢驗的原理
ADF檢驗就是判斷序列是否存在單位根：如果序列平穩，就不存在單位根；否則，就會存在單位根。

所以，ADF檢驗的 H0 假設就是存在單位根，如果得到的顯著性檢驗統計量小於三個置信度（10%，5%，1%），則對應有（90%，95，99%）的把握來拒絕原假設。

ADF檢驗的python實現
ADF檢驗可以通過python中的 statsmodels 模塊，這個模塊提供了很多統計模型。

使用方法如下：

導入adfuller函數

from statsmodels.tsa.stattools import adfuller
adfuller函數的參數意義分別是：

x：一維的數據序列。
maxlag：最大滯後數目。
regression：回歸中的包含項（c：只有常數項，預設；ct：常數項和趨勢項；ctt：常數項，線性二次項；nc：沒有常數項和趨勢項）
autolag：自動選擇滯後數目（AIC：赤池信息準則，預設；BIC：貝葉斯信息準則；t-stat：基於maxlag，從maxlag開始並刪除一個滯後直到最後一個滯後長度基於 t-statistic 顯著性小於5%為止；None：使用maxlag指定的滯後）
store：True  False，預設。
regresults：True 完整的回歸結果將返回。False，預設。
返回值意義為：

adf：Test statistic，T檢驗，假設檢驗值。
pvalue：假設檢驗結果。
usedlag：使用的滯後階數。
nobs：用於ADF回歸和計算臨界值用到的觀測值數目。
icbest：如果autolag不是None的話，返回最大的信息準則值。
resstore：將結果合併為一個dummy。

 adf概念    refer    原文鏈接：https://blog.csdn.net/FrankieHello/java/article/details/86766625

（2）判斷

adfuller(dta)後我得到的return；

Test Statistic 0.815369
p_value 0.991880
#Lags Used 13.000000
Number of Observation Uesd 130.000000
Critical Value(1%) -3.481682
Critical Value(5%) -2.884042
Critical Value(10%) -2.578770
dtype: float64

如何確定該序列能否平穩呢？主要看：

1%、%5、%10不同程度拒絕原假設的統計值和ADF Test result的比較，ADF Test result同時小於1%、5%、10%即說明非常好地拒絕該假設，本數據中，adf結果（Test Statistic）為0.8， 大於三個level的統計值。

看P-value是否非常接近0.  本數據中，P-value 為 0.99,不夠接近0.

ADF檢驗的原假設是存在單位根，只要這個統計值是小於1%水平下的數字就可以極顯著的拒絕原假設，認為數據平穩。註意，ADF值一般是負的，也有正的，但是它只有小於1%水平下的才能認為是及其顯著的拒絕原假設。

對於ADF結果在1% 以上 5%以下的結果，也不能說不平穩，關鍵看檢驗要求是什麼樣子的。

但是對於本例，，數據是顯然不平穩的了。

2020-05-24