1、數據冗餘導致的問題:冗餘存儲、更新異常、插入異常、刪除異常。 2、函數依賴:一種完整性約束。 在關係模式r(R)中,α屬於R,β屬於R。 1)α函數確定β(β函數依賴於α):記作α→β,對於任意合法關係r及其中任兩個元組ti和tj,i≠j,若ti[α]=tj[α],則ti[β]=tj[β]。 2 ...
1、數據冗餘導致的問題:冗餘存儲、更新異常、插入異常、刪除異常。
2、函數依賴:一種完整性約束。
在關係模式r(R)中,α屬於R,β屬於R。
1)α函數確定β(β函數依賴於α):記作α→β,對於任意合法關係r及其中任兩個元組ti和tj,i≠j,若ti[α]=tj[α],則ti[β]=tj[β]。
2)非平凡函數依賴和平凡函數依賴:若α→β,但β不屬於α,則稱α→β是非平凡函數依賴;否則,若β不屬於α,則稱α→β是平凡函數依賴。

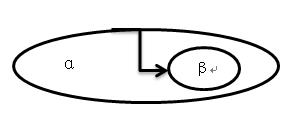
非平凡函數依賴 平凡函數依賴
3)完全函數依賴和部分函數依賴:α→β是非平凡函數依賴,若對任意的γ含於α,γ→β都不成立,則稱α→β是完全函數依賴,簡稱完全依賴;否則,若存在非空的γ含於α,使γ→β成立,則稱α→β是部分函數依賴,簡稱部分依賴。
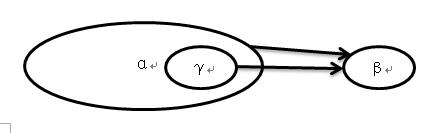
部分依賴α→β的依賴圖
4)傳遞函數依賴
γ屬於R,若α→β,β→γ,則必存在函數依賴α→γ,若α→β,β→γ和α→γ都是非平凡函數依賴,且β不依賴於α,則稱α→γ是傳遞函數依賴,簡稱傳遞依賴。
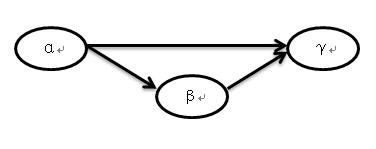
傳遞依賴α→γ的依賴圖
3、函數依賴集閉包
1)邏輯蘊涵:若給定函數依賴集F,可以證明其他函數依賴也成立,則稱這些函數依賴被F邏輯蘊涵。
2)閉包:令F為一函數依賴集,F邏輯蘊涵的所有函數依賴組成的集合稱為F的閉包,記為F+。
3)屬性集A的閉包:令r(R)為關係模式,F為屬性依賴集,A屬於R的屬性集,則稱在函數依賴集F下由A函數確定的所有屬性的集合為F下屬性集A的閉包,記為A+。
4)Armstrong公理及推論(可直接計算F+)
(1)自反律:若存在β屬於α,則有α→β。
(2)增補律:若存在α→β,則有γα→γβ。
(3)傳遞律:若存在α→β且β→γ,則有α→γ。
(4)合併律:若存在α→β且α→γ,則有α→βγ。
(5)分解律:若存在α→βγ,則有α→β和α→γ。
(6)偽傳遞律:若存在α→β且βγ→δ,則有αγ→δ。
4、範式(關係模式要滿足的條件)
1)目的:消除存儲異常、減少數據冗餘、保證數據完整性和存儲效率。
2)基於函數依賴理論,範式的分類:
(1)第一範式(1NF)---碼
如果一關係模式r(R)的每個屬性對應的域值都是不可分的,則稱r(R)屬於第一範式。
目標:將基本數據劃分成稱為實體集或表的邏輯單元,當設計好每個實體後,需要為其指定主碼。
| empno | ename | address | ||
| province | city | street | ||
非規範化的關係模式(地址的值域可分)
| empno | ename | province | city | street |
1NF規範化後的關係模式
(2)第二範式(2NF)---全部是碼
如果一關係模式r(R),α屬於r(R),若α包含在r(R)的摸個候選碼中,則稱α為主屬性,否則α非主屬性。
如果一關係模式r(R)屬於第一範式,且所有非主屬性都完全函數依賴於r(R)的候選碼,則稱r(R)屬於第二範式。
目標:將只部分依賴於候選碼(即依賴於候選碼的部分屬性)的非主屬性通過關係模式分解移到其他表中去。
(3)第三範式(3NF)---僅僅是碼
如果一關係模式r(R)屬於第二範式,且所有非主屬性都直接函數依賴於r(R)的候選碼,且非主屬性之間不存在依賴關係(即不存在非主屬性傳遞依賴於候選碼),則稱r(R)屬於第三範式。
目標:將只部分依賴於候選碼(即依賴於候選碼的部分屬性)的非主屬性通過關係模式分解移到其他表中去。
(4)Boyce-Codd範式(BCNF)
給定關係模式r(R)及函數依賴集F,若F+中的所有函數依賴α→β(α屬於R,β屬於R)至少滿足下列條件之一:α→β是平凡函數依賴(即β屬於α)、α是r(R)的一個超碼(即α+包含R的全部屬性),則稱r(R)屬於Boyce-Codd範式。



