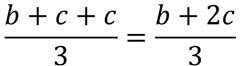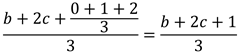演算法（第四版）C#題解——2.1

来源:https://www.cnblogs.com/ikesnowy/archive/2018/01/02/8178698.html
-Advertisement-
Play Games

寫在前面 整個項目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp 這一節內容可能會用到的庫文件有 Sort和 SortData，同樣在 Github 上可以找到。 善用 Ctrl + F 查找題目 ...


寫在前面

整個項目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp

這一節內容可能會用到的庫文件有 Sort和 SortData，同樣在 Github 上可以找到。

善用 Ctrl + F 查找題目。

習題&題解

2.1.1

題目

按照演算法 2.1 所示軌跡的格式給出選擇排序是如何將數組 E A S Y Q U E S T I O N 排序的。

解答

2.1.1

 

2.1.2

題目

在選擇排序中，一個元素最多可能會被交換多少次？平均可能會被交換多少次？

解答

最多會被交換 n 次，只要將一個有序數列迴圈右移一位就可以構造這樣的情況。

例如：

2.1.2

平均每個元素被交換了 N/N=1 次。（總共 N 個元素，總共發生了 N 次交換）

 

2.1.3

題目

構造一個含有 N 個元素的數組，使選擇排序（演算法 2.1）運行過程中 a[j] < a[min] （由此 min 會不斷更新）成功的次數最大。

解答

你需要一個逆序的數組。

例如：9 8 7 6 5 4 3 2 1

i=0 條件滿足 8 次，1 和 9 交換，1 8 7 6 5 4 3 2 9。

i=1 條件滿足 6 次，2 和 8 交換，1 2 7 6 5 4 3 8 9。

i=2 條件滿足 4 次，3 和 7 交換，1 2 3 6 5 4 7 8 9。

i=3 條件滿足 2 次，4 和 6 交換。1 2 3 4 5 6 7 8 9。

一共滿足了 8+6+4+2=20 次

 

2.1.4

題目

按照演算法 2.2 所示軌跡的格式給出插入排序是如何將數組 E A S Y Q U E S T I O N 排序的。

解答

2.1.4

 

2.1.5

題目

構造一個含有 N 個元素的數組，使插入排序（演算法 2.2）運行過程中內迴圈（for）的兩個判斷結果總是假。

解答

條件是：

j > 0 && less(a[j], a[j - 1])

第一個條件屬於迴圈計數用的條件，與數組元素無關；

第二個條件當 a[j] 和 a[j - 1] 是一組逆序對時滿足，因此這個條件總是為假 = 數組沒有逆序對 = 數組有序。

因此只要輸入已經排好序的數組即可。

逆序對：指序列中順序相反的兩個數，例如 1 2 3 4 5 7 6 8 9 中的 7 6。

 

2.1.6

題目

在所有主鍵都相同時，選擇排序和插入排序誰更快？

解答

插入排序更快。

選擇排序無論如何都需要 n + (n-1) + (n-2) + …  + 1 = n^2/2 次比較。

插入排序在這種情況下只需要 n 次比較。（所有主鍵相同 = 數組已排序）

 

2.1.7

題目

對於逆序數組，選擇排序和插入排序誰更快？

解答

假設比較的開銷小於等於交換的開銷，此時選擇排序更快，具體比較見下表。

  比較次數 交換次數
插入排序 ~N^2/2 ~N^2/2
選擇排序 ~N^2/2 N
 

2.1.8

題目

假設元素只可能有三種值，使用插入排序處理這樣一個隨機數組的運行時間是線性的還是平方級別的？或是介於兩者之間？

解答

平方級別。

如果數組中元素各不相同，那麼這個結論很容易證明（一般的插入排序）。

接下來我們證明有重覆元素的情況下，這個結論仍然成立：

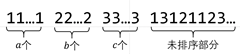
首先對於插入排序過程中的某一時刻，我們有下圖這樣的一般情況：

image

其中，1，2，3 分別代表三種不同的取值以及其先後順序。

假設這是第 i 次插入前，如果第 i 次插入的是 1，我們需要交換 b+c 次，插入 2 則需要交換 c 次，插入 3 則不需要交換。

根據題意，這是一個隨機數組，我們假設其為均勻分佈，那麼三種取值的出現幾率相等。

第 i 次插入所需要的平均交換次數即為：

2.1.8

第 i 次插入後，b + 2c 視插入的元素不同會出現不同的變化：

如果插入的是 1，那麼 b+2c 的值不會變化。

如果插入的是 2，那麼 b+2c 的值增加 1。

如果插入的是 3，那麼 b+2c 的值增加 2。

同樣由於三種取值的概率相等，我們得出第 i + 1 次插入平均需要交換的次數為：

2.1.8.2

也就是說，平均每次插入都會使下一次插入的交換次數增加 1/3。

令 i=0，此時交換次數為 0，i+1 的交換次數即為 1/3，i+2 的交換次數即為 2/3，以此類推。

我們可以得出總交換次數：

2.1.8.3

由此證明，在元素取值為 3 種且出現概率相等時，插入排序的交換開銷時平方級別的。

比較開銷和交換開銷類似，一般情況下比較次數=交換次數+1，除非插入的數是已知最小的數（移動到最左側），這個時候比較次數和交換次數相等。

因此比較次數=交換次數+N-e，e 是一個不大於 N 的數，代表插入的數是已知最小的數這種情況發生的次數。

根據上式可以得出結論：在元素取值為 3 種且出現概率相等時，插入排序的比較開銷也是平方級別的。

綜合兩個結論即可證明插入排序的開銷在題目描述的情況下是平方級別的。

證明完畢。

 

2.1.9

題目

按照演算法 2.3 所示軌跡的格式給出希爾排序是如何將數組 E A S Y S H E L L S O R T Q U E S T I O N 排序的。

解答

2.1.9

 

2.1.10

題目

在希爾排序中為什麼在實現 h 有序時不使用選擇排序？

解答

對於部分有序的數組，插入排序比選擇排序快。

這個結論可以在中文版 P158， 英文版 P252 找到。

 

2.1.11

題目

將希爾排序中實時計算遞增序列改為預先計算並存儲在一個數組中。

解答

希爾排序的官方實現：https://algs4.cs.princeton.edu/21elementary/Shell.java.html

只要稍作修改即可，詳情見代碼。

代碼
/// <summary>
        /// 利用希爾排序將數組按升序排序。
        /// </summary>
        /// <param name="a">需要排序的數組。</param>
        public override void Sort<T>(T[] a)
        {
            int n = a.Length;
            int[] h = new int[2];   // 預先準備好的 h 值數組

            int hTemp = 1;
            int sequenceSize = 0;
            for (sequenceSize = 0; hTemp < n; sequenceSize++)
            {
                if (sequenceSize >= h.Length)  // 如果數組不夠大則雙倍擴容
                {
                    int[] expand = new int[h.Length * 2];
                    for (int j = 0; j < h.Length; j++)
                    {
                        expand[j] = h[j];
                    }
                    h = expand;
                }
                h[sequenceSize] = hTemp;
                hTemp = hTemp * 3 + 1;
            }

            for (int t = sequenceSize - 1; t >= 0; t--)
            {
                for (int i = h[t]; i < n; i++)
                {
                    for (int j = i; j >= h[t] && Less(a[j], a[j - h[t]]); j -= h[t])
                    {
                        Exch(a, j, j - h[t]);
                    }
                }
                Debug.Assert(IsHSorted(a, h[t]));
            }
            Debug.Assert(IsSorted(a));
        }

 

2.1.12

題目

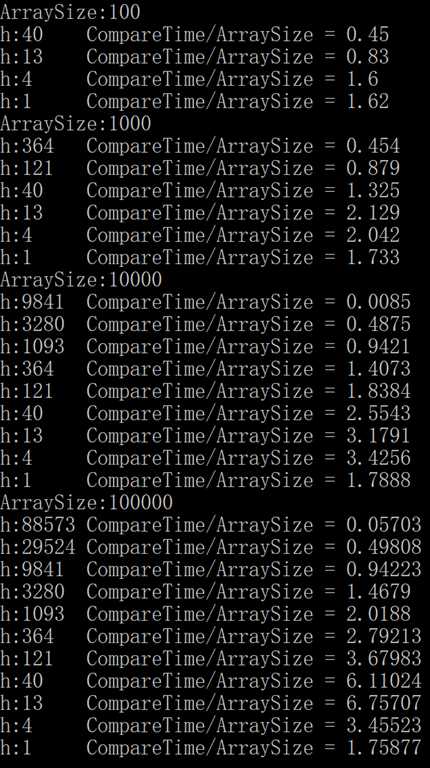
令希爾排序列印出遞增序列的每個元素所帶來的比較次數和數組大小的比值。
編寫一個測試用例對隨機 Double 數組進行希爾排序，驗證該值是一個小常數，數組大小按照 10 的冪次遞增，不小於 100。

解答

結果截圖如下，同一個 h 值對應的比值在數組大小不同時保持為一個小常數：

image

代碼
class Program
{
    // 查看最後結果
    // 可以發現相同的 h 在數組大小不同時所產生的比值十分接近。
    static void Main(string[] args)
    {
        Random random = new Random();
        ShellSort sort = new ShellSort();

        int size = 100;
        for (int i = 0; i < 5; i++)
        {
            double[] a = new double[size];
            for (int j = 0; j < size; j++)
            {
                a[j] = random.NextDouble() * 100;
            }
            Console.WriteLine("ArraySize:" + size);
            sort.Sort(a);
            size *= 10;
        }
    }
}

 

2.1.13

題目

紙牌排序。

說說你會如何將一副撲克牌按花色排序（花色排序是黑桃、紅桃、梅花和方片），
限制條件是所有牌都是背面朝上排成一列，而你一次只能翻看兩張牌或者交換兩張牌（保持背面朝上）。

解答

可以用冒泡排序做，具體方法如下：

翻一二兩張，是逆序對就交換，否則什麼也不做
翻二三兩張，是逆序對就交換，否則什麼也不做
一直到最後，可以保證最右側的是最大花色的牌
然後不斷重覆上述過程，就可以完全排序

 

2.1.14

題目

出列順序。

說說你會如何將一副撲克牌排序，
限制條件是只能查看最上面的兩張牌，交換最上面的兩張牌，或是將最上面的一張牌放到這摞牌的最下麵。

解答

用一種類似於冒泡的方法做，具體步驟為：

重覆以下步驟，直到全部完成一遍之後沒有發生交換
    重覆以下步驟 n-1 次
        如果頂端兩張牌逆序，那麼交換它們。
        將第一張牌放到牌堆底部。

具體步驟圖：

InkedWP_20171126_21_29_53_Pro_LI2

我們將牌排成一個環，用一支筆隔開，這裡我們標記筆的左側是牌堆頂部，右側是牌堆底部。

那麼我們能做的三個操作在這裡即為：

查看最上面兩張牌 = 從筆的位置開始，逆時針查看兩張牌。

交換最上面兩張牌 = 從筆的位置開始，逆時針選擇兩張牌並交換。

將最上面的一張牌放到最下麵 = 將筆的位置逆時針移動一位。

 

下麵我們開始執行開始說過的操作，目標順序是自頂向下從小到大排列。

初始情況如圖所示：

WP_20171126_21_23_47_Pro_LI

梅花7 和 紅桃4 不是逆序對，直接將筆逆時針移動一位。

WP_20171126_21_24_07_Pro_LI

紅桃4 和 黑桃6 不是逆序對，我們將筆逆時針移動一位。

WP_20171126_21_24_42_Pro_LI

再看 黑桃6 和 方片A，是逆序對，我們交換並將筆逆時針移動一位。

WP_20171126_21_24_56_Pro_LI

再看 黑桃6 和 紅桃J，是逆序對，我們交換並將筆逆時針移動一位。

WP_20171126_21_25_09_Pro_LI

現在我們已經操作了 4 次，內部迴圈結束，我們將筆放回初始位置。

WP_20171126_21_25_19_Pro_LI

這樣一次迴圈之後，我們就把最大的牌放在了最下麵，依次類推即可完全排序。

 

2.1.15

題目

昂貴的交換。

一家貨運公司的一位職工得到了一項任務，需要將若幹大貨箱按照發貨時間擺放。
比較發貨時間很容易（對照標簽即可），但將兩個貨箱交換位置則很困難（移動麻煩）。
倉庫已經快滿了，只有一個空閑的倉位。這位職員應該使用哪種排序演算法呢？

解答

選擇排序

交換（也就是 Exch() 方法）需要一個額外空間，這裡的條件滿足。

現在我們應該使交換次數最少，選擇排序只需要 N 次交換，比插入排序平均 N^2/4 少（N > 2）。

 

2.1.16

題目

驗證。

編寫一個 check() 方法，調用 sort() 對任意數組排序。
如果排序成功而且數組中的所有對象均沒有被修改則返回 true，否則返回 false。
不要假設 sort() 只能通過 exch() 來移動數據，可以信任並使用 Array.sort()。

解答

如果移動數據時新建了對象，那麼雖然值沒有改變，但是數組中的對象被修改了。

代碼

插入排序中的 Exch() 換成瞭如下方式：

string temp = new string(s[i].ToCharArray());
s[i] = s[min];
s[min] = temp;

全部程式代碼如下：

using System;

namespace _2._1._16
{
    /*
     * 2.1.16
     * 
     * 驗證。
     * 編寫一個 check() 方法，
     * 調用 sort() 對任意數組排序。
     * 如果排序成功而且數組中的所有對象均沒有被修改則返回 true，
     * 否則返回 false。
     * 不要假設 sort() 只能通過 exch() 來移動數據，
     * 可以信任並使用 Array.sort()。
     * 
     */
    public class Program
    {
        static void Main(string[] args)
        {
            string[] test = new string[5] { "a", "b", "d", "c", "e" };
            Console.WriteLine(CheckArraySort(test));
            Console.WriteLine(CheckSelectionSort(test));
        }

        /// <summary>
        /// 測試 Array.Sort() 方法。
        /// </summary>
        /// <param name="a">用於測試的數組。</param>
        /// <returns>如果數組對象沒有改變，返回 true，否則返回 false。</returns>
        static bool CheckArraySort(string[] a)
        {
            string[] backup = new string[a.Length];
            a.CopyTo(backup, 0);

            Array.Sort(a);

            foreach (string n in a)
            {
                bool isFind = false;
                for (int i = 0; i < a.Length; i++)
                {
                    if (ReferenceEquals(n, backup[i]))
                    {
                        isFind = true;
                        break;
                    }
                }
                if (!isFind)
                {
                    return false;
                }
            }

            return true;
        }

        /// <summary>
        /// 測試選擇排序。
        /// </summary>
        /// <param name="a">用於測試的數組。</param>
        /// <returns>如果數組對象沒有改變，返回 true，否則返回 false。</returns>
        static bool CheckSelectionSort(string[] a)
        {
            string[] backup = new string[a.Length];
            a.CopyTo(backup, 0);

            SelectionSort(a);

            foreach (string n in a)
            {
                bool isFind = false;
                for (int i = 0; i < a.Length; i++)
                {
                    if (ReferenceEquals(n, backup[i]))
                    {
                        isFind = true;
                        break;
                    }
                }
                if (!isFind)
                {
                    return false;
                }
            }

            return true;
        }

        /// <summary>
        /// 選擇排序，其中的交換部分使用新建對象並複製的方法。
        /// </summary>
        /// <param name="s">用於排序的數組。</param>
        public static void SelectionSort(string[] s)
        {
            for (int i = 0; i < s.Length; i++)
            {
                int min = i;
                for (int j = i + 1; j < s.Length; j++)
                {
                    if (s[j].CompareTo(s[min]) < 0)
                    {
                        min = j;
                    }
                }
                string temp = new string(s[i].ToCharArray());
                s[i] = s[min];
                s[min] = temp;
            }
        }
    }
}

 

2.1.17

題目

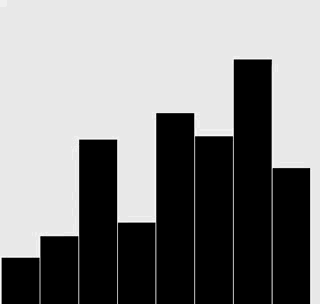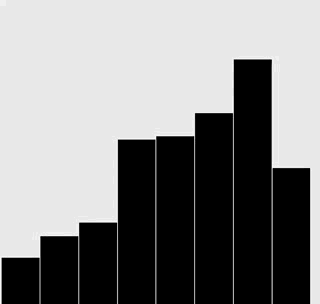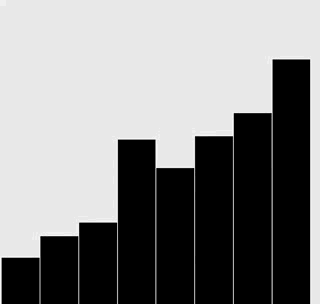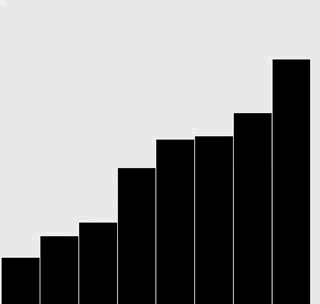
動畫。

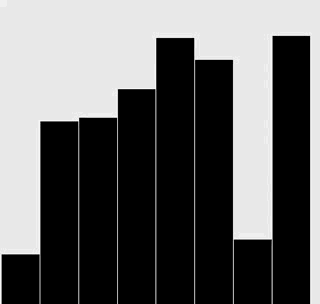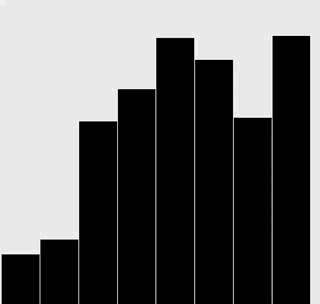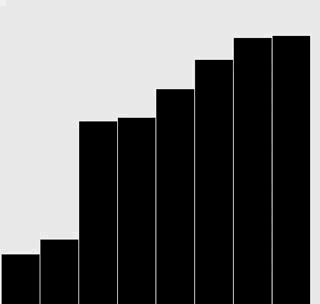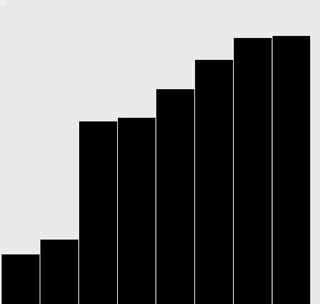
修改插入排序和選擇排序的代碼，使之將數組內容繪製成正文中所示的棒狀圖。
在每一輪排序後重繪圖片來產生動畫效果，並以一張“有序”的圖片作為結束，即所有的圓棒均已按照高度有序排列。
提示：使用類似於正文中的用例來隨機生成 Double 值，在排序代碼的適當位置調用 show() 方法，併在 show() 方法中清理畫布並繪製棒狀圖。

解答

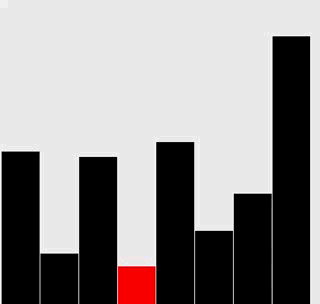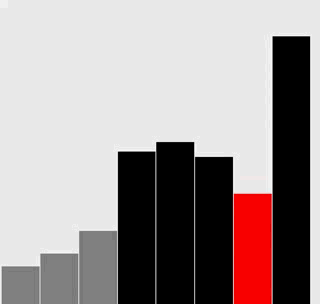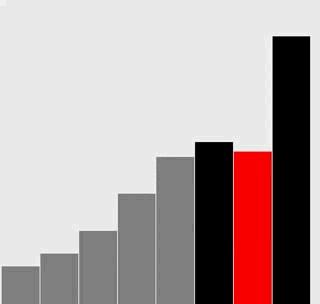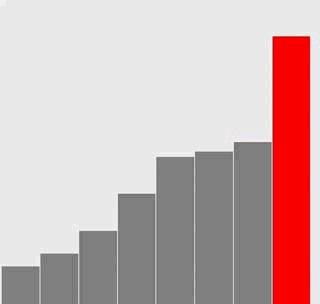
選擇排序：

選擇排序

插入排序：

插入排序

代碼

使用一個 timer 按一定時間重繪數組，排序演算法裡面一次迴圈後等待一段時間再進行下一次迴圈。

這裡排序演算法是另開線程運行的，防止 Sleep 的時候讓程式無響應。

選擇排序：

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Threading;

namespace _2._1._17
{
    public partial class Form2 : Form
    {
        double[] randomDoubles;
        public Form2(int N)
        {
            InitializeComponent();
            this.randomDoubles = new double[N];
            Random random = new Random();
            for (int i = 0; i < N; i++)
            {
                this.randomDoubles[i] = random.NextDouble() * 0.8 + 0.2;
            }
            drawPanel();

            this.timer1.Interval = 60;
            this.timer1.Start();

            Thread thread = new Thread(new ThreadStart(this.SelectionSort));
            thread.IsBackground = true;
            thread.Start();
        }

        /// <summary>
        /// 選擇排序。
        /// </summary>
        private void SelectionSort()
        {
            for (int i = 0; i < this.randomDoubles.Length; i++)
            {
                int min = i;
                for (int j = i; j < this.randomDoubles.Length; j++)
                {
                    if (this.randomDoubles[min] > this.randomDoubles[j])
                    {
                        min = j;
                    }
                }
                double temp = this.randomDoubles[i];
                this.randomDoubles[i] = this.randomDoubles[min];
                this.randomDoubles[min] = temp;
                Thread.Sleep(1000);
            }
        }

        /// <summary>
        /// 在屏幕上用柱形圖繪製數組。
        /// </summary>
        private void drawPanel()
        {
            Graphics graphics = this.CreateGraphics();
            graphics.Clear(this.BackColor);
            graphics.TranslateTransform(0, this.Height);
            graphics.ScaleTransform(1, -1);
            Rectangle clientRect = this.ClientRectangle;
            Rectangle drawRect = new Rectangle(clientRect.X + 10, clientRect.Y + 10, clientRect.Width - 10, clientRect.Height - 10);

            PointF[] barX = new PointF[this.randomDoubles.Length];
            float unitX = (float)drawRect.Width / this.randomDoubles.Length;
            unitX -= 4;

            barX[0] = new PointF(4, drawRect.Top);
            for (int i = 1; i < this.randomDoubles.Length; i++)
            {
                barX[i] = new PointF(2 + unitX + barX[i - 1].X, drawRect.Top);
            }

            RectangleF[] bars = new RectangleF[this.randomDoubles.Length];
            for (int i = 0; i < this.randomDoubles.Length; i++)
            {
                SizeF size = new SizeF(unitX, (float)this.randomDoubles[i] * drawRect.Height);
                bars[i] = new RectangleF(barX[i], size);
            }

            graphics.FillRectangles(Brushes.Black, bars);
            graphics.Dispose();
        }

        private void timer1_Tick(object sender, EventArgs e)
        {
            drawPanel();
        }
    }
}

插入排序：

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Threading;

namespace _2._1._17
{
    public partial class Form3 : Form
    {
        double[] randomDoubles;
        public Form3(int N)
        {
            InitializeComponent();
            this.randomDoubles = new double[N];
            Random random = new Random();
            for (int i = 0; i < N; i++)
            {
                this.randomDoubles[i] = random.NextDouble() * 0.8 + 0.2;
            }
            drawPanel();

            this.timer1.Interval = 60;
            this.timer1.Start();

            Thread thread = new Thread(new ThreadStart(this.InsertionSort));
            thread.IsBackground = true;
            thread.Start();
        }

        /// <summary>
        /// 插入排序。
        /// </summary>
        private void InsertionSort()
        {
            for (int i = 0; i < this.randomDoubles.Length; i++)
            {
                for (int j = i; j > 0 && this.randomDoubles[j] < this.randomDoubles[j - 1]; j--)
                {
                    double temp = this.randomDoubles[j];
                    this.randomDoubles[j] = this.randomDoubles[j - 1];
                    this.randomDoubles[j - 1] = temp;
                    Thread.Sleep(500);
                }
            }
        }

        /// <summary>
        /// 在屏幕上用柱形圖繪製數組。
        /// </summary>
        private void drawPanel()
        {
            Graphics graphics = this.CreateGraphics();
            graphics.Clear(this.BackColor);
            graphics.TranslateTransform(0, this.Height);
            graphics.ScaleTransform(1, -1);
            Rectangle clientRect = this.ClientRectangle;
            Rectangle drawRect = new Rectangle(clientRect.X + 10, clientRect.Y + 10, clientRect.Width - 10, clientRect.Height - 10);

            PointF[] barX = new PointF[this.randomDoubles.Length];
            float unitX = (float)drawRect.Width / this.randomDoubles.Length;
            unitX -= 4;

            barX[0] = new PointF(4, drawRect.Top);
            for (int i = 1; i < this.randomDoubles.Length; i++)
            {
                barX[i] = new PointF(2 + unitX + barX[i - 1].X, drawRect.Top);
            }

            RectangleF[] bars = new RectangleF[this.randomDoubles.Length];
            for (int i = 0; i < this.randomDoubles.Length; i++)
            {
                SizeF size = new SizeF(unitX, (float)this.randomDoubles[i] * drawRect.Height);
                bars[i] = new RectangleF(barX[i], size);
            }

            graphics.FillRectangles(Brushes.Black, bars);
            graphics.Dispose();
        }

        private void timer1_Tick(object sender, EventArgs e)
        {
            drawPanel();
        }
    }
}

 

2.1.18

題目

可視軌跡。
修改你為上一題給出的解答，為插入排序和選擇排序生成和正文中類似的可視軌跡。
提示：使用 setYscale() 函數是一個明智的選擇。
附加題：添加必要的代碼，與正文中的圖片一樣用紅色和灰色強調不同角色的元素。

解答

選擇排序

選擇排序

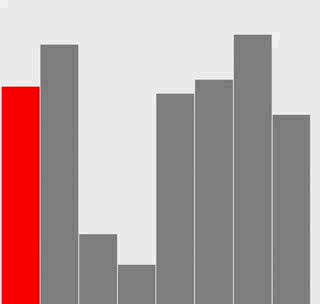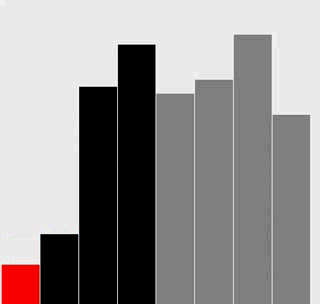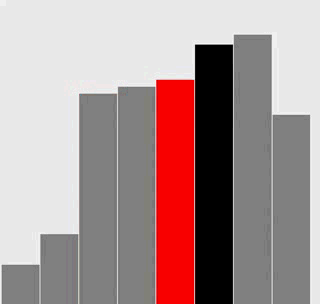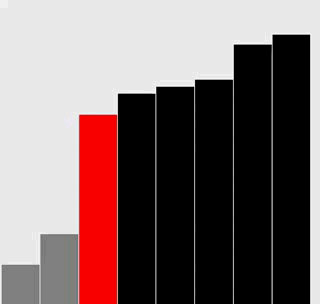
插入排序

插入排序

代碼

與上題類似，但要特別標出移動的元素。

選擇排序：

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Threading;

namespace _2._1._18
{
    public partial class Form2 : Form
    {
        double[] randomDoubles;
        int sortI;
        int sortJ;
        int sortMin;
        public Form2(int N)
        {
            InitializeComponent();
            this.randomDoubles = new double[N];
            Random random = new Random();
            for (int i = 0; i < N; i++)
            {
                this.randomDoubles[i] = random.NextDouble() * 0.8 + 0.2;
            }
        }

        /// <summary>
        /// 選擇排序。
        /// </summary>
        private void SelectionSort()
        {
            for (this.sortI = 0; this.sortI < this.randomDoubles.Length; this.sortI++)
            {
                this.sortMin = this.sortI;
                for (this.sortJ = this.sortI; this.sortJ < this.randomDoubles.Length; this.sortJ++)
                {
                    if (this.randomDoubles[this.sortMin] > this.randomDoubles[this.sortJ])
                    {
                        this.sortMin = this.sortJ;
                    }
                }
                drawPanel();
                double temp = this.randomDoubles[this.sortI];
                this.randomDoubles[this.sortI] = this.randomDoubles[this.sortMin];
                this.randomDoubles[this.sortMin] = temp;
                Thread.Sleep(1000);
            }
        }

        /// <summary>
        /// 繪製柱形圖。
        /// </summary>
        private void drawPanel()
        {
            Graphics graphics = this.CreateGraphics();
            graphics.Clear(this.BackColor);
            graphics.TranslateTransform(0, this.Height);
            graphics.ScaleTransform(1, -1);
            Rectangle clientRect = this.ClientRectangle;
            Rectangle drawRect = new Rectangle(clientRect.X + 10, clientRect.Y + 10, clientRect.Width - 10, clientRect.Height - 10);

            PointF[] barX = new PointF[this.randomDoubles.Length];
            float unitX = (float)drawRect.Width / this.randomDoubles.Length;
            unitX -= 4;

            barX[0] = new PointF(4, drawRect.Top);
            for (int i = 1; i < this.randomDoubles.Length; i++)
            {
                barX[i] = new PointF(2 + unitX + barX[i - 1].X, drawRect.Top);
            }

            RectangleF[] bars = new RectangleF[this.randomDoubles.Length];
            for (int i = 0; i < this.randomDoubles.Length; i++)
            {
                SizeF size = new SizeF(unitX, (float)this.randomDoubles[i] * drawRect.Height);
                bars[i] = new RectangleF(barX[i], size);
            }

            for (int i = 0; i < bars.Length; i++)
            {
                if (i == this.sortMin)
                {
                    graphics.FillRectangle(Brushes.Red, bars[i]);
                }
                else if (i < this.sortI)
                {
                    graphics.FillRectangle(Brushes.Gray, bars[i]);
                }
                else
                {
                    graphics.FillRectangle(Brushes.Black, bars[i]);
                }
            }
            graphics.Dispose();
        }

        private void Form2_Shown(object sender, EventArgs e)
        {
            SelectionSort();
        }
    }
}

插入排序

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Threading;

namespace _2._1._18
{
    public partial class Form3 : Form
    {
        double[] randomDoubles;
        int sortI;
        int sortJ;
        int n = 0;
        public Form3(int N)
        {
            InitializeComponent();
            this.randomDoubles = new double[N];
            Random random = new Random();
            for (int i = 0; i < N; i++)
            {
                this.randomDoubles[i] = random.NextDouble() * 0.8 + 0.2;
            }
        }

        /// <summary>
        /// 插入排序。
        /// </summary>
        private void InsertionSort()
        {
            for (this.sortI = 0; this.sortI < this.randomDoubles.Length; this.sortI++)
            {
                for (this.sortJ = this.sortI; this.sortJ > 0 && this.randomDoubles[this.sortJ] < this.randomDoubles[this.sortJ - 1]; this.sortJ--)
                {
                    double temp = this.randomDoubles[this.sortJ];
                    this.randomDoubles[this.sortJ] = this
您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 基於java的ssh架構的2018最新 酒店信息管理系統【原創】-未經同意請勿轉載
    網路上流傳的大部分95%以上的程式都是跑不通的，應大部分同學要求，現寫了一個酒店管理信息系統。 是ssh的架構， 基於java的 。 貼2個截圖 第二個 ...
  • 洛谷P2044 [NOI2012]隨機數生成器
    題目描述 棟棟最近迷上了隨機演算法，而隨機數是生成隨機演算法的基礎。棟棟準備使用線性同餘法（Linear Congruential Method）來生成一個隨機數列，這種方法需要設置四個非負整數參數m,a,c,X[0],按照下麵的公式生成出一系列隨機數{Xn}： 其中mod m表示前面的數除以m的餘數。 ...
  • 寫給小白的JAVA鏈接MySQL資料庫的步驟(JDBC):
    作為複習總結的筆記,我羅列了幾個jdbc步驟,後邊舉個簡單的例子,其中的try塊請讀者自行處理. /* * 1.下載驅動包:com.mysql.jdbc.Driver;網上很多下載資源,自己找度娘,此處不再提供; * * 2.將驅動包導入項目,並add to build path,具體步驟去問度娘. ...
  • 【ASP.NET MVC系列】淺談NuGet在VS中的運用
    一 概述 在我們講解NuGet前，我們先來看看一個例子。 1.例子： 假設現在開發一套系統，其中前端框架我們選擇Bootstrap,由於選擇Bootstrap作為前端框架，因此，在項目中，我們需要引入Bootstrap相關文件，大致會執行如下操作。 步驟一：下載Bootstrap文件 輸入Boots ...
  • .NET反射用戶定義枚舉類型
    示例代碼： 執行結果圖： ...
  • 往Oracle資料庫中插入NCLOB/CLOB類型數據
    最近因為業務需求開發了一個介面用於接收數據，但是總有一些數據報出ORA-01704：字元串文字太長錯誤。仔細排查後發現，竟然是NCLOB類型欄位提示這個錯誤。NCLOB存儲空間有4G，怎麼也想不明白為什麼會報這個錯誤。原來因為介面插入數據採用字元串拼接的方式。 而oracle中會把字元串轉為varc ...
  • 調用API讓音效卡發出聲音
    1.定義一個枚舉，樂器類型 #region 樂器定義 public enum MusicNo:uint { /// <summary> /// //大鋼琴 /// </summary> AcousticGrandPiano = 0, /// <summary> ///明亮的鋼琴 /// </summ ...
  • .NET使用DAO.NET實體類模型操作資料庫
    一、新建項目 打開vs2017，新建一個項目，命名為orm1 二、新建資料庫 打開 SqlServer資料庫，新建資料庫 orm1，並新建表 student 。 三、新建 ADO.NET 實體數據模型 這裡點擊 新建連接，新建資料庫連接。其實伺服器名輸入 . 代表本地伺服器，身份驗證選擇預設的Win ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類